Mathematics
Prove that the quadrilateral obtained by joining the mid-points of an isosceles trapezium is a rhombus.
Rectilinear Figures
8 Likes
Answer
P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively.
Join AC and BD.

Since, ABCD is an isosceles trapezium
Its diagonals are equal.
AC = BD = x (let)
Now, in ∆ABC
P and Q are the mid-points of AB and BC
So, PQ || AC and PQ = AC = x (By midpoint theorem) … (i)
Similarly, in ∆ADC
S and R mid-point of AD and CD
So, SR || AC and SR = AC = x (By midpoint theorem) … (ii)
From (i) and (ii), we have
PQ || SR and PQ = SR = …….(iii)
In ∆CBD,
R and Q are the mid-points of CD and BC
So, QR || BD and QR = BD = x (By midpoint theorem) … (iv)
Similarly, in ∆ABD
S and P mid-point of AD and AB
So, SP || BD and SP = BD = x (By midpoint theorem) … (v)
From (iv) and (v), we have
QR || SP and QR = SP = …….(vi)
From (iii) and (vi) we get,
PQ = QR = SR = SP and QR || SP, PQ || SR.
So, sides of PQRS are equal and opposite sides are parallel.
Hence, proved that PQRS is a rhombus.
Answered By
4 Likes
Related Questions
Find the size of each lettered angle in the following figure.
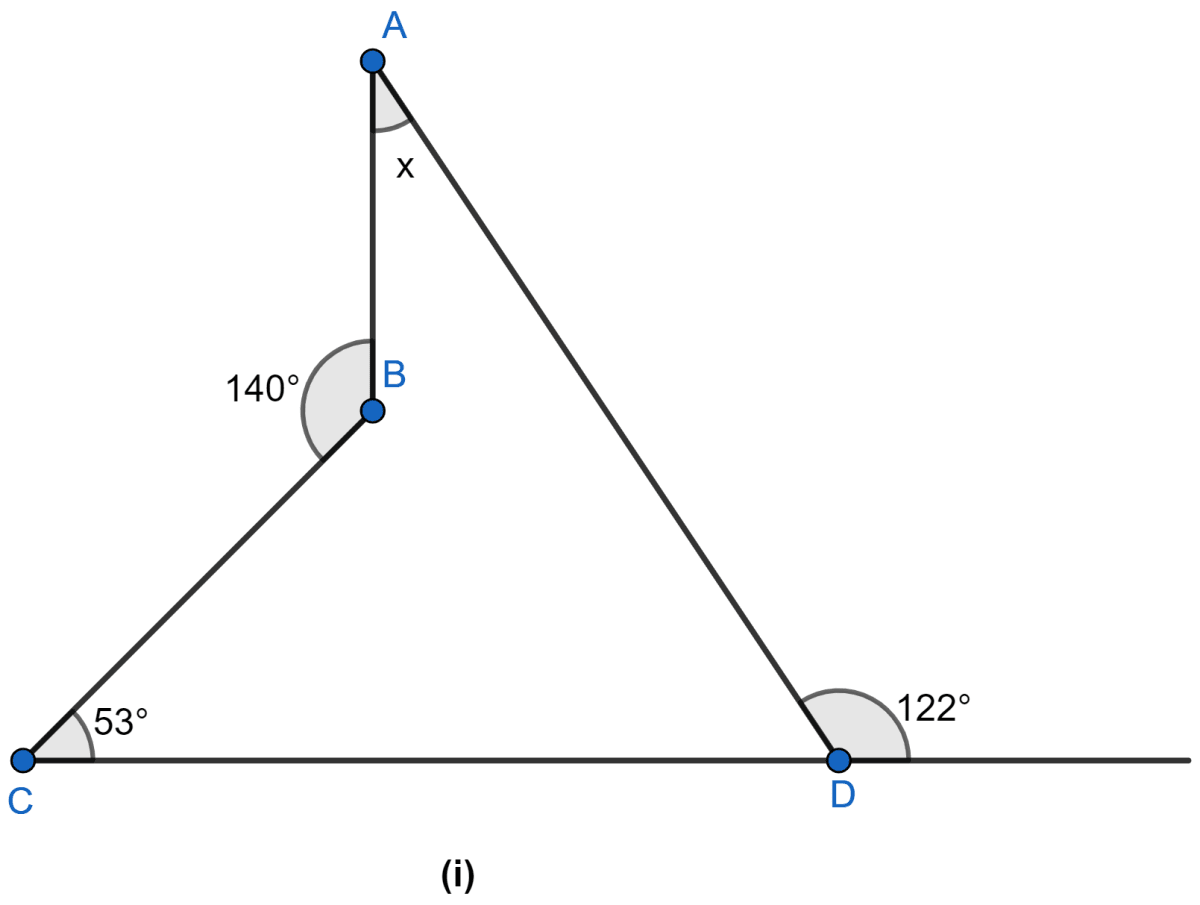
Find the size of each lettered angle in the following figure.

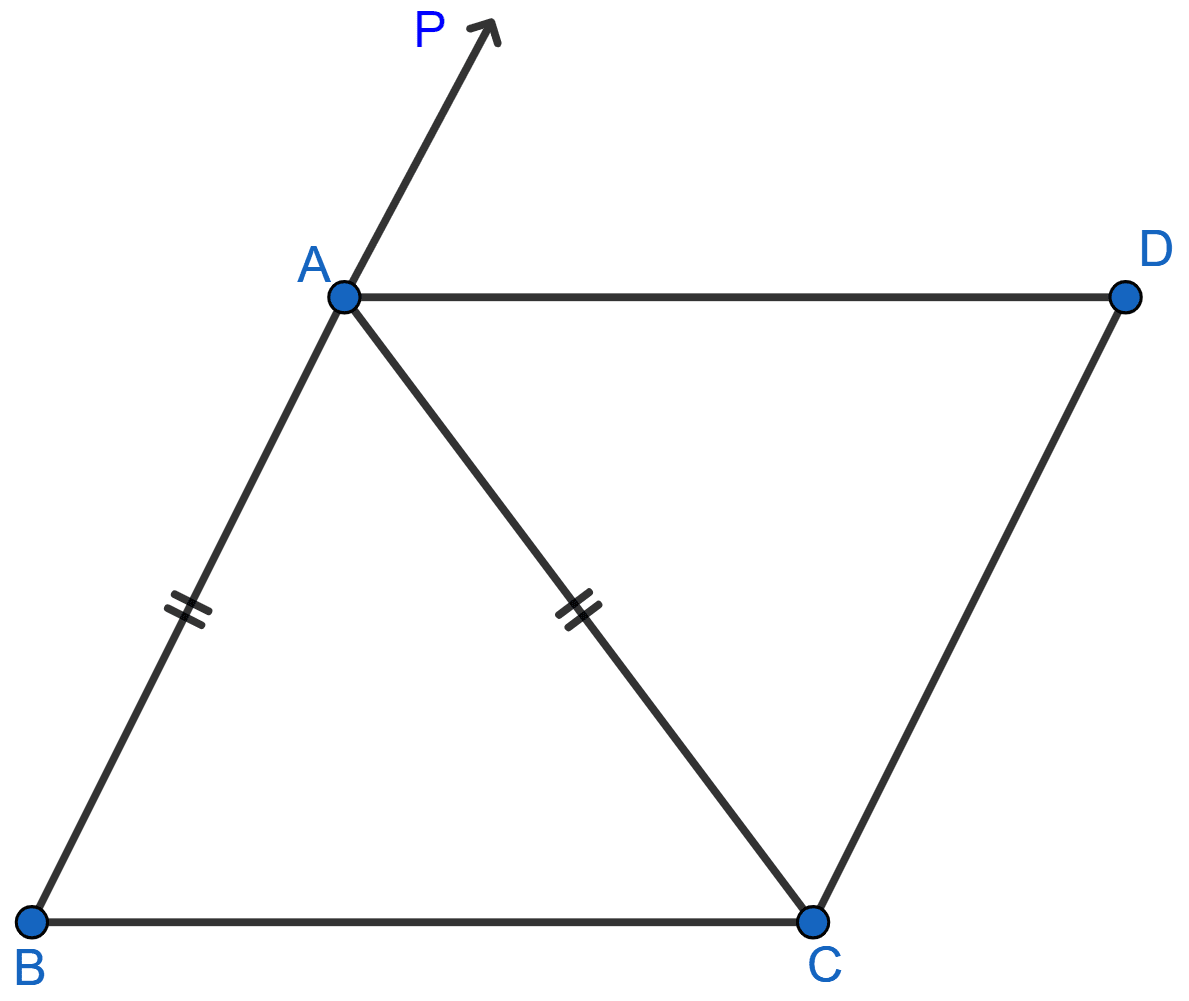
In the adjoining figure, ABC is an isosceles triangle in which AB = AC. AD bisects exterior angle PAC and CD || BA. Show that
(i) ∠DAC = ∠BCA
(ii) ABCD is a parallelogram.
In the adjoining figure, ABCD is a parallelogram. CB is produced to E such that BE = BC. Prove that AEBD is a parallelogram.
