Prove that the bisectors of the interior angles of a rectangle form a square.

In rectangle,

All the interior angles equal to 90°. So, bisectors divide interior angles into two 45° angles.

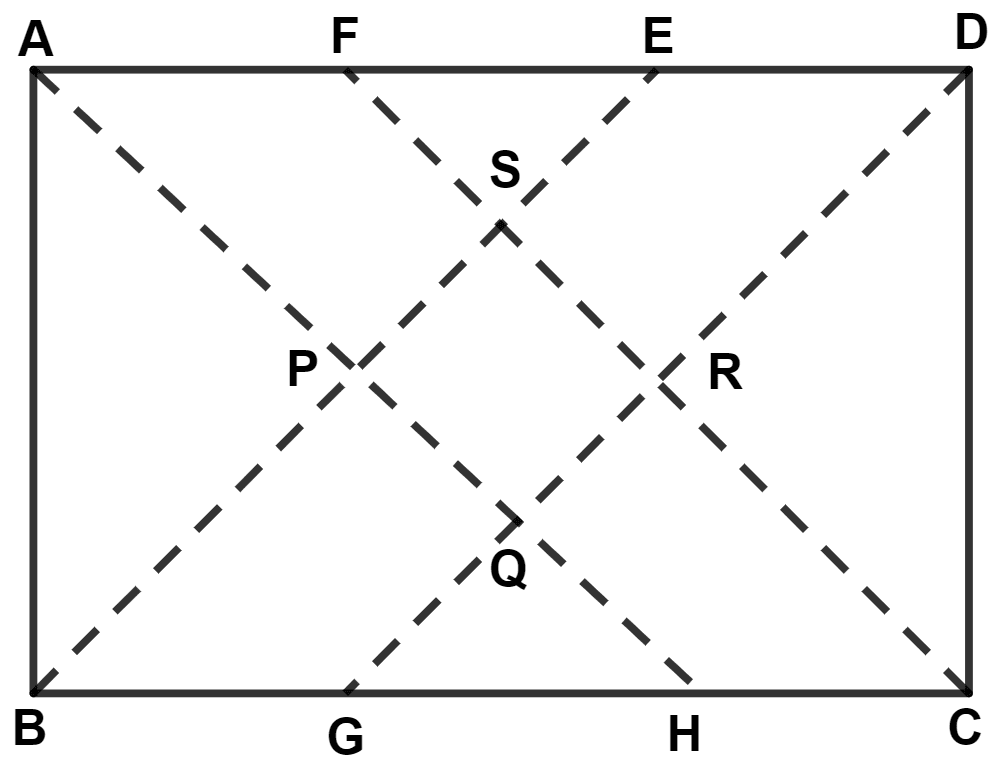
In △ BSC,

By angle sum property of triangle,

⇒ ∠SBC + ∠SCB + ∠BSC = 180°

⇒ $\dfrac{∠B}{2} + \dfrac{∠C}{2}$ + ∠BSC = 180°

⇒ 45° + 45° + ∠BSC = 180°

⇒ ∠BSC = 180° - 90° = 90°.

Since,

⇒ ∠SBC = ∠SCB

∴ BS = SC (Sides opposite to equal angles are equal) …..(1)

From figure,

⇒ ∠PSR = ∠BSC = 90°.

In △ APB and △ DRC,

⇒ ∠PAB = ∠RDC (Both equal to 45°)

⇒ ∠PBA = ∠RCD (Both equal to 45°)

⇒ AB = CD (Opposite sides of rectangle are equal)

∴ △ APB ≅ △ DRC (By A.S.A. axiom)

We know that,

Corresponding parts of congruent triangle are equal.

∴ BP = CR ………(2)

Subtracting equation (2) from (1), we get :

⇒ BS - BP = SC - CR

⇒ PS = SR ………….(3)

In △ DRC,

By angle sum property of triangle,

⇒ ∠RCD + ∠CDR + ∠DRC = 180°

⇒ $\dfrac{∠C}{2} + \dfrac{∠D}{2}$ + ∠DRC = 180°

⇒ 45° + 45° + ∠DRC = 180°

⇒ ∠DRC = 180° - 90° = 90°.

From figure,

⇒ ∠SRQ = ∠DRC = 90° (Vertically opposite angles are equal)

In △ PAB,

By angle sum property of triangle,

⇒ ∠PAB + ∠ABP + ∠BPA = 180°

⇒ $\dfrac{∠A}{2} + \dfrac{∠B}{2}$ + ∠BPA = 180°

⇒ 45° + 45° + ∠BPA = 180°

⇒ ∠BPA = 180° - 90° = 90°.

From figure,

⇒ ∠SPQ = ∠BPA = 90° (Vertically opposite angles are equal)

In △ AQD,

By angle sum property of triangle,

⇒ ∠DAQ + ∠QDA + ∠AQD = 180°

⇒ $\dfrac{∠A}{2} + \dfrac{∠D}{2}$ + ∠AQD = 180°

⇒ 45° + 45° + ∠AQD = 180°

⇒ ∠AQD = 180° - 90° = 90°.

Since,

⇒ ∠DAQ = ∠QDA

∴ AQ = QD (Sides opposite to equal angles are equal) …..(4)

From figure,

⇒ ∠PQR = ∠AQD = 90°.

Since, △ APB ≅ △ DRC

∴ AP = DR ………(5)

Subtracting equation (5) from (4), we get :

⇒ AQ - AP = QD - DR

⇒ PQ = QR ………..(6)

In △ BSC and △ AQD,

⇒ ∠B = ∠A (Both equal to 45°)

⇒ ∠C = ∠D (Both equal to 45°)

⇒ ∠S = ∠Q (Both equal to 90°)

∴ △ BSC ≅ △ AQD (By A.A.A. axiom)

We know that,

Corresponding parts of congruent triangle are equal.

∴ BS = AQ ………(7)

In △ AQD,

⇒ ∠A = ∠D (Both equal to 45°)

⇒ DQ = AQ (Sides opposite to equal angles are equal) ………(8)

From equation (7) and (8), we get :

⇒ BS = DQ ………(9)

In △ CDR,

⇒ ∠C = ∠D (Both equal to 45°)

⇒ DR = CR (Sides opposite to equal angles are equal) ………(10)

From equation (2) and (10), we get :

⇒ BP = DR …..(11)

Subtracting equation (11) from (9), we get :

⇒ BS - BP = DQ - DR

⇒ PS = QR ………(12)

From equation (3), (6) and (12), we get :

⇒ PQ = QR = RS = PS.

Since, all sides of quadrilateral PQRS are equal and each interior angle equals to 90°.

∴ PQRS is a square.

Hence, proved that bisectors of the interior angles of a rectangle form a square.