Prove that the bisectors of opposite angles of a parallelogram are parallel.

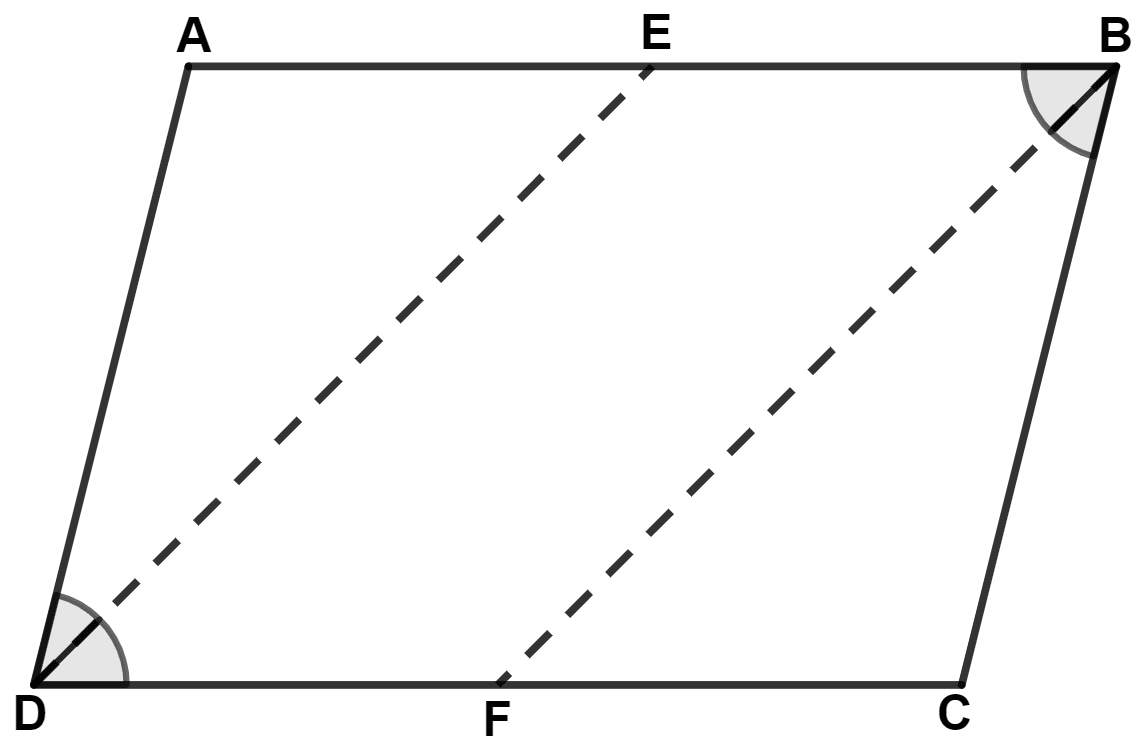
From figure,

DE and BF are bisectors of angles D and B respectively.

In parallelogram ABCD,

⇒ ∠B = ∠D (Opposite angles of || gm are equal)

⇒ $\dfrac{∠B}{2} = \dfrac{∠D}{2}$

⇒ ∠FBC = ∠ADE.

In △ ADE and △ CBF,

⇒ ∠ADE = ∠FBC (Proved above)

⇒ AD = BC (Opposite sides of || gm ABCD are equal)

⇒ ∠DAE = ∠BCF (Opposite angles of || gm ABCD are equal)

∴ △ ADE ≅ △ CBF (By A.S.A. axiom)

We know that,

Corresponding sides of congruent triangle are equal.

∴ AE = CF

Since, AE = CF and AB = CD,

∴ BE = DF

In parallelogram ABCD,

⇒ AB || CD

⇒ BE || DF

Since,

BE = DF and BE || DF

In quadrilateral BEDF, one of the pair of opposite sides are equal and parallel.

∴ BEDF is a parallelogram.

∴ DE || BF.

Hence, proved that bisectors of opposite angles of a parallelogram are parallel.