Mathematics
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Answer
In the below figure, P, Q, R, S are points of contact
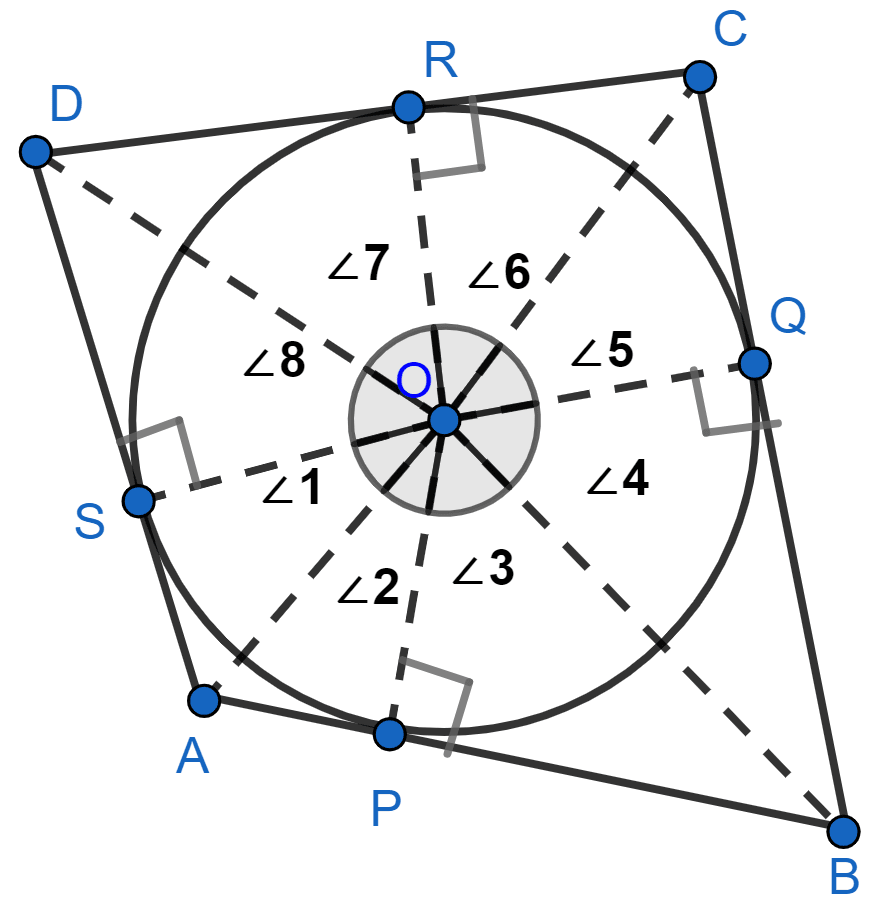
We know that,
The tangents drawn from an external point to a circle are equal.
AS = AP
We know that,
Tangents drawn from a point outside the circle, subtend equal angles at the centre.
∠1 = ∠2, ∠3 = ∠4, ∠5 = ∠6, ∠7 = ∠8.
Since complete angle is 360° at the centre,
We have,
⇒ ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°
⇒ ∠1 + ∠1 + ∠4 + ∠4 + ∠5 + ∠5 + ∠8 + ∠8 = 360° or ∠2 + ∠2 + ∠3 + ∠3 + ∠6 + ∠6 + ∠7 + ∠7 = 360°
⇒ 2(∠1 + ∠8 + ∠4 + ∠5) = 360° or 2 (∠2 + ∠3 + ∠6 + ∠7) = 360°
⇒ ∠1 + ∠8 + ∠4 + ∠5 = 180° or ∠2 + ∠3 + ∠6 + ∠7 = 180° …………(1)
From above figure,
∠1 + ∠8 = ∠AOD, ∠4 + ∠5 = ∠BOC and ∠2 + ∠3 = ∠AOB, ∠6 + ∠7 = ∠COD
Substituting above values in equation (1), we get :
⇒ ∠AOD + ∠BOC = 180° or ∠AOB + ∠COD = 180°
∠AOD and ∠BOC are angles subtended by opposite sides of quadrilateral circumscribing a circle and the sum of the two is 180°.
Hence, proved that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Related Questions
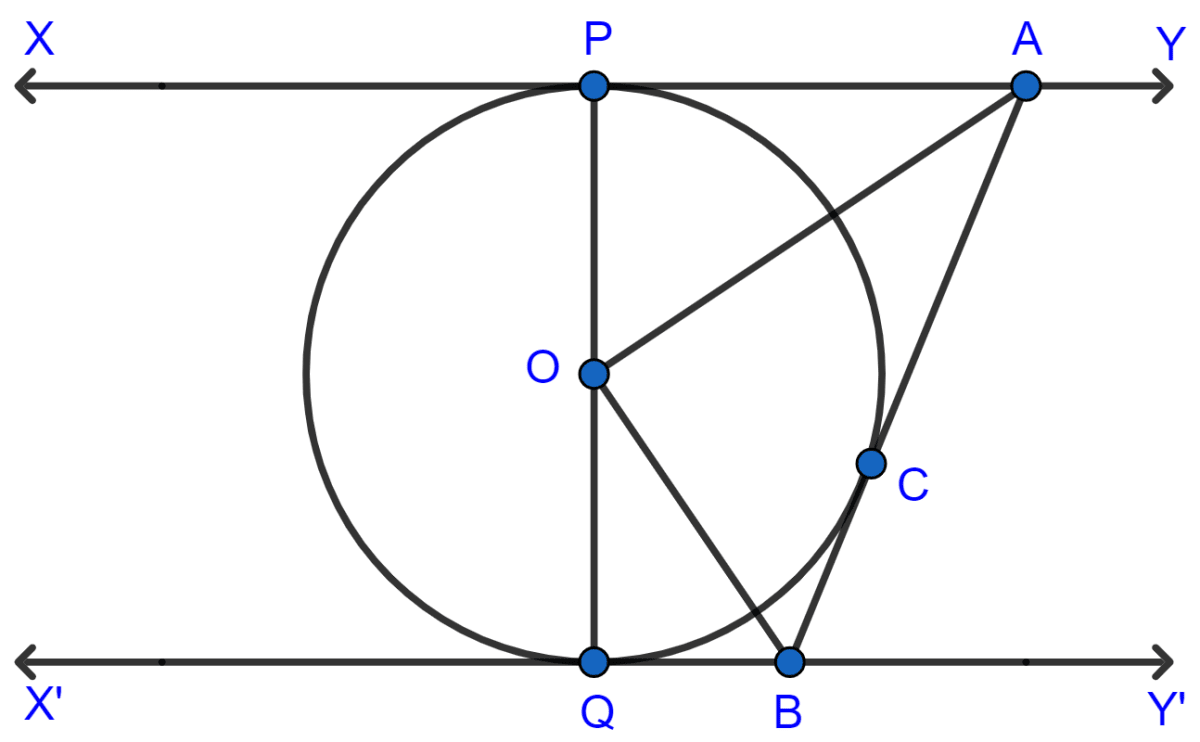
In the given figure, XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X'Y' at B. Prove that ∠AOB = 90°.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
Prove that the parallelogram circumscribing a circle is a rhombus.
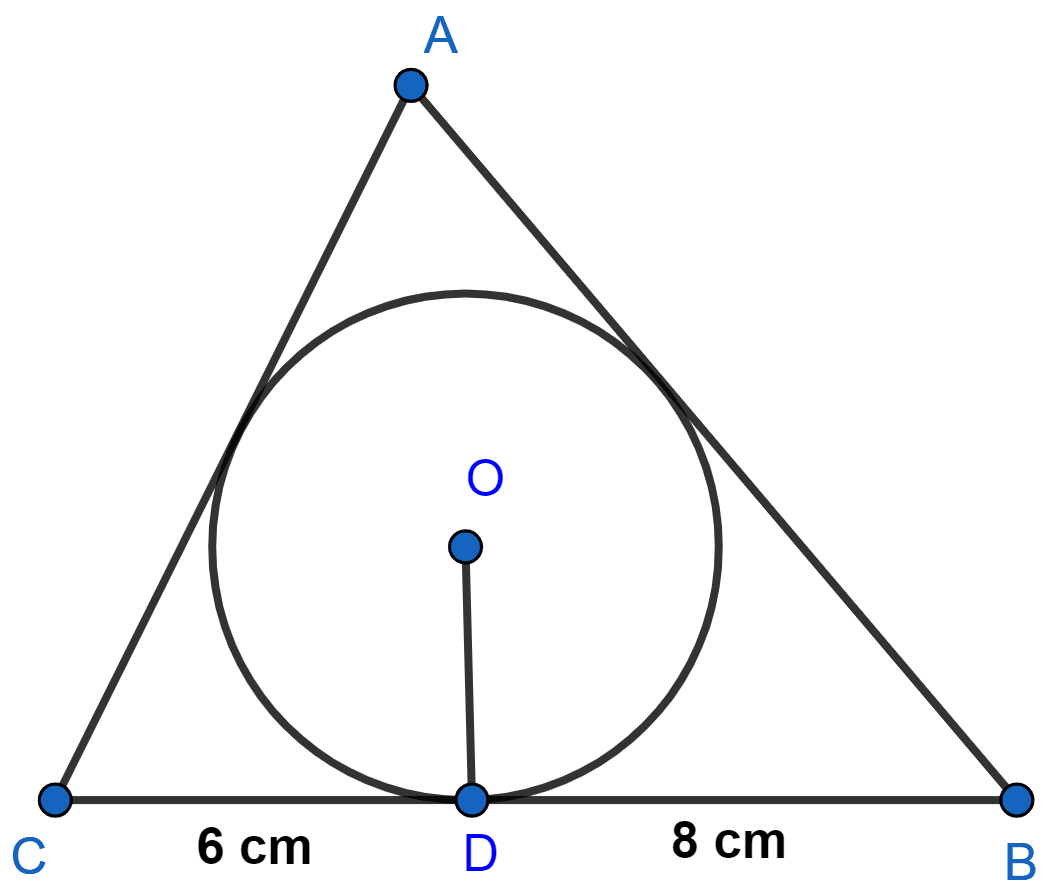
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively in figure. Find the sides AB and AC.