Mathematics
Prove that every diagonal of a rhombus bisects the angles at the vertices.
Answer
From figure,
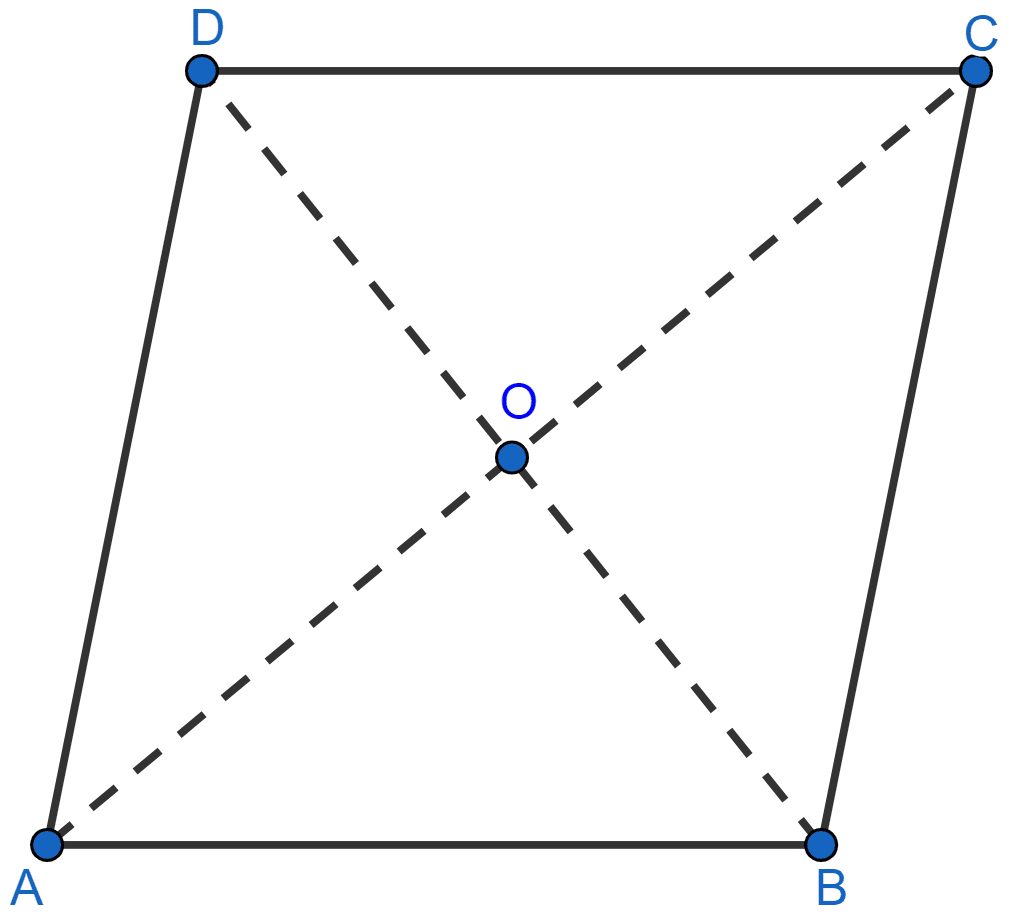
In △AOD and △COD,
AD = CD (All sides of rhombus are equal)
DO = OD (Common sides)
AO = OC (Diagonals of rhombus bisect each other)
∴ △AOD ≅ △COD (By SSS rule of congruency)
∴ ∠ADO = ∠CDO (By C.P.C.T.)
∴ BD bisects ∠D.
In △AOB and △COB,
AB = BC (All sides of rhombus are equal)
BO = OB (Common sides)
AO = OC (Diagonals of rhombus bisect each other)
∴ △AOB ≅ △COB (By SSS rule of congruency)
∴ ∠ABO = ∠CBO (By C.P.C.T.)
∴ BD bisects ∠B.
In △AOB and △AOD,
AB = AD (All sides of rhombus are equal)
AO = OA (Common sides)
OD = OB (Diagonals of rhombus bisect each other)
∴ △AOB ≅ △AOD (By SSS rule of congruency)
∴ ∠OAD = ∠OAB (By C.P.C.T.)
∴ AC bisects ∠A.
In △BOC and △DOC,
BC = CD (All sides of rhombus are equal)
OC = CO (Common sides)
OD = OB (Diagonals of rhombus bisect each other)
∴ △BOC ≅ △DOC (By SSS rule of congruency)
∴ ∠OCD = ∠OCB (By C.P.C.T.)
∴ AC bisects ∠C.
Hence, proved that every diagonal of a rhombus bisects the angles at the vertices.
Related Questions
ABCD is a parallelogram. If the diagonal AC bisects ∠A, then prove that :
(i) AC bisects ∠C
(ii) ABCD is a rhombus
(iii) AC ⊥ BD
If the angle of a quadrilateral are equal, prove that it is a rectangle.
Prove that bisectors of any two adjacent angles of a parallelogram are at right angles.
If the diagonals of a rhombus are equal, prove that it is a square.