Mathematics
Answer
Let ABCD be a cyclic parallelogram.
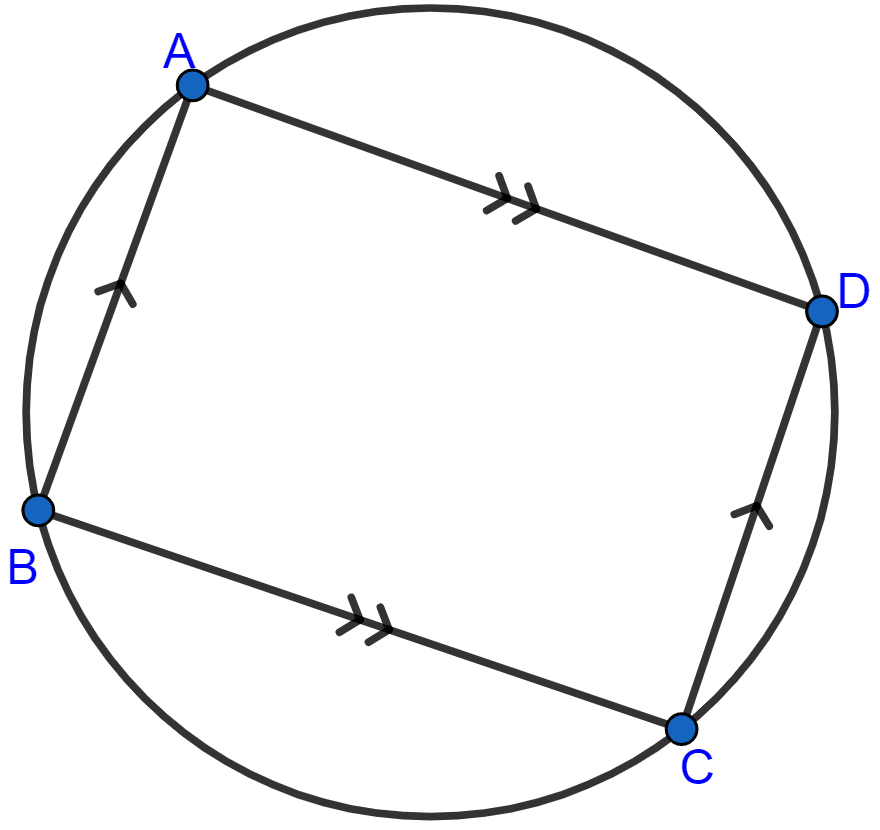
In parallelogram opposite angles are equal.
∴ ∠A = ∠C and ∠B = ∠D.
Sum of opposite angles of a cyclic quadrilateral is 180°
⇒ ∠A + ∠C = 180°
⇒ ∠A + ∠A = 180°
⇒ 2∠A = 180°
⇒ ∠A = 90°.
∴ ∠C = 90°.
Similarly,
⇒ ∠B + ∠D = 180°
⇒ ∠B + ∠B = 180°
⇒ 2∠B = 180°
⇒ ∠B = 90°.
∴ ∠D = 90°.
Hence, ∠A = ∠B = ∠C = ∠D = 90°.
In parallelogram opposite sides are equal i.e. AD = BC and AB = CD.
Hence, ABCD is a rectangle as opposite sides are equal and all the angles are equal to 90°.
Related Questions
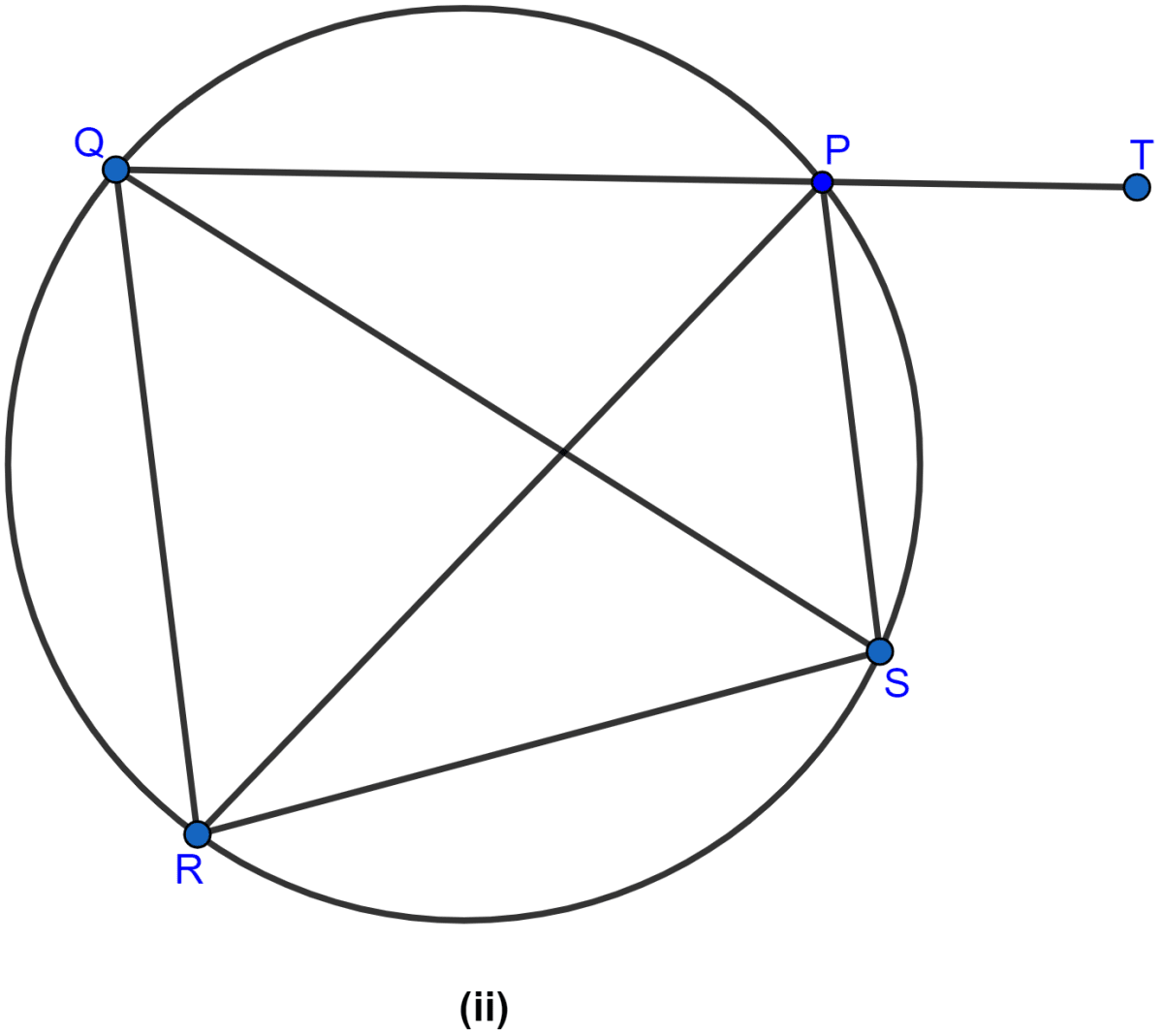
In the figure (ii) given below, SP is the bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that SQ = RS.
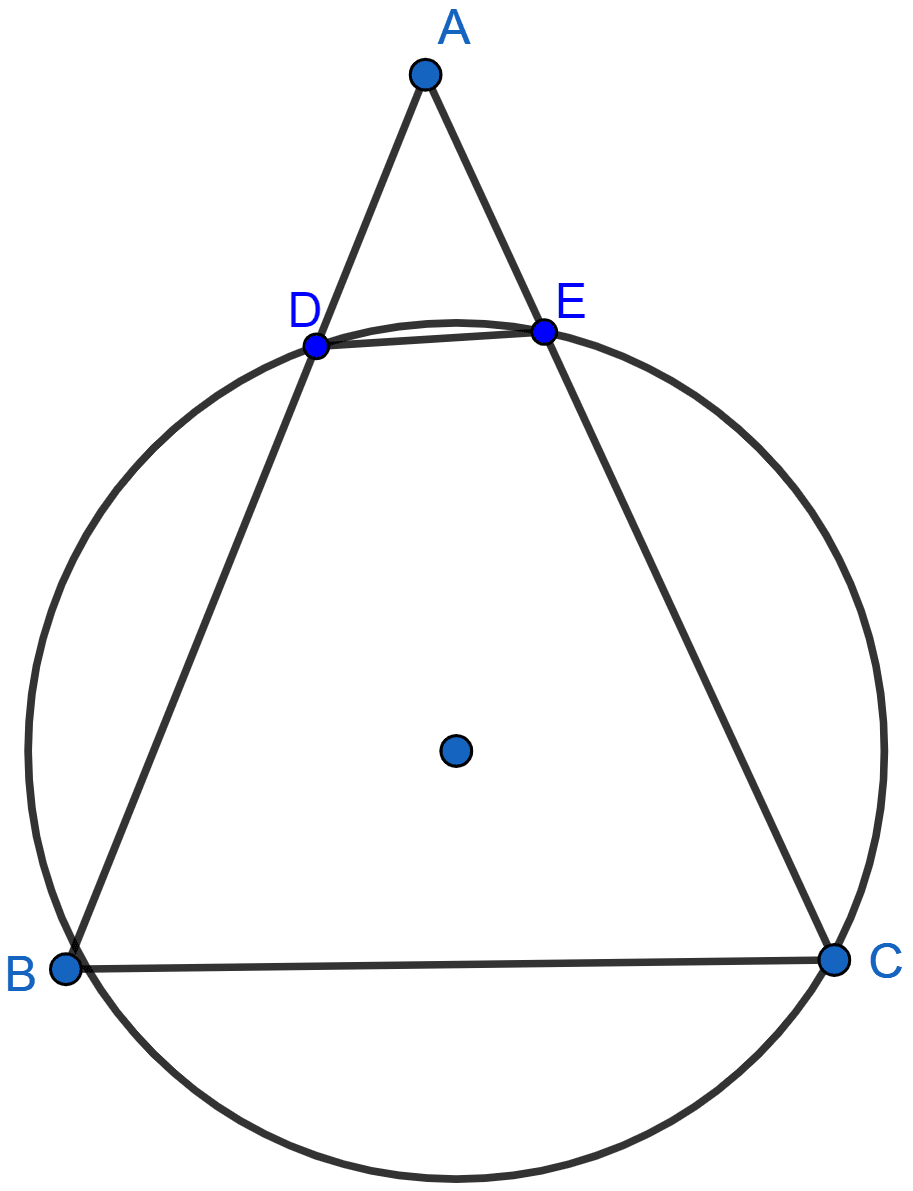
In the adjoining figure, ABC is an isosceles triangle in which AB = AC and circle passing through B and C intersects sides AB and AC at points D and E. Prove that DE || BC.
Prove that a cyclic rhombus is a square.