Mathematics
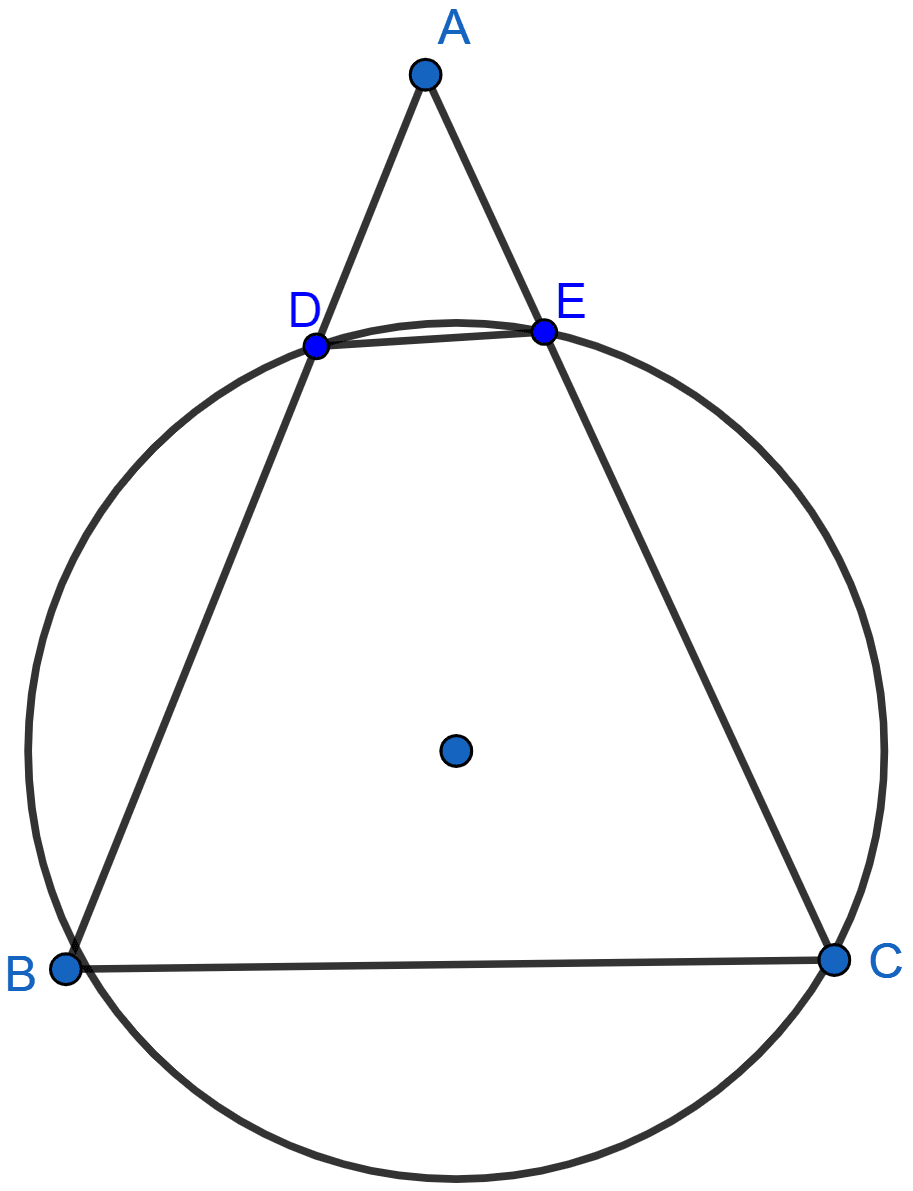
In the adjoining figure, ABC is an isosceles triangle in which AB = AC and circle passing through B and C intersects sides AB and AC at points D and E. Prove that DE || BC.
Circles
30 Likes
Answer
Given, AB = AC
∴ ∠ABC = ∠ACB (As angles opposite to equal sides are equal)
As BCED is a cyclic quadrilateral,
∠ADE = ∠BCE (∵ exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.)
∴ ∠ADE = ∠ABC
Since these angles are equal and are corresponding this is the property of parallel lines,
∴ DE || BC.
Hence, proved that DE || BC.
Answered By
23 Likes
Related Questions
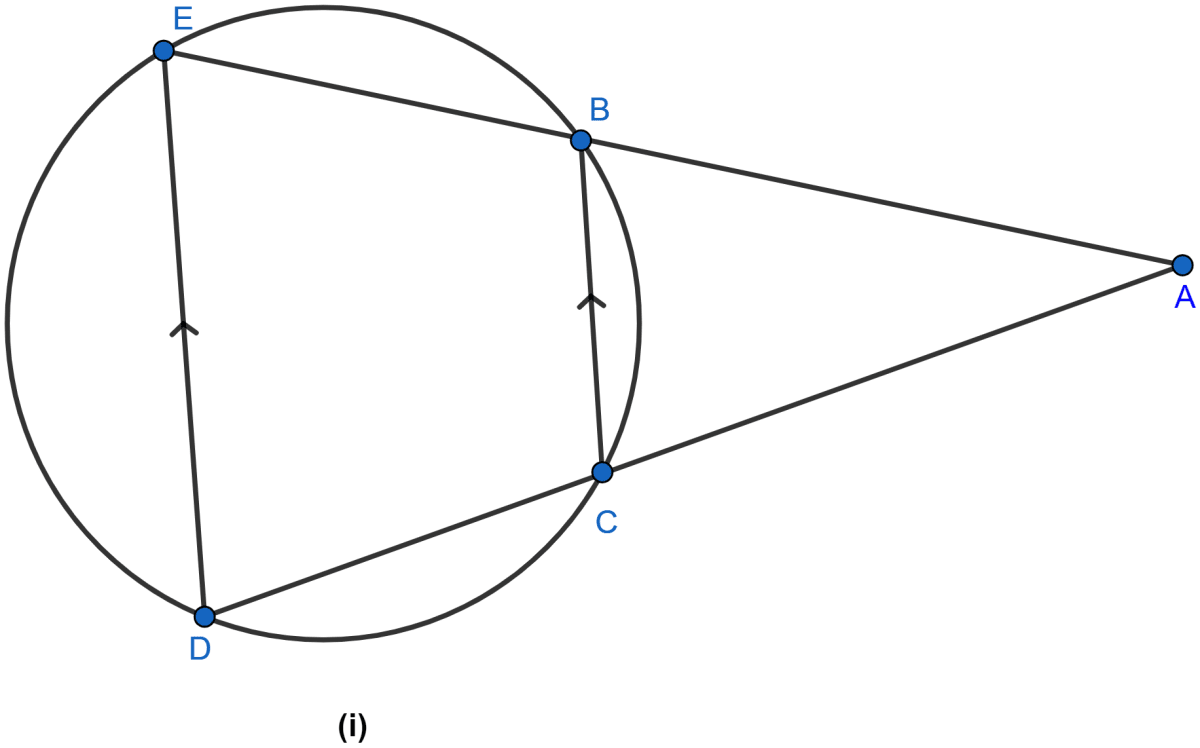
In the figure (i) given below, ED and BC are two parallel chords of the circle and ABE, ACD are two st. lines. Prove that AED is an isosceles triangle.
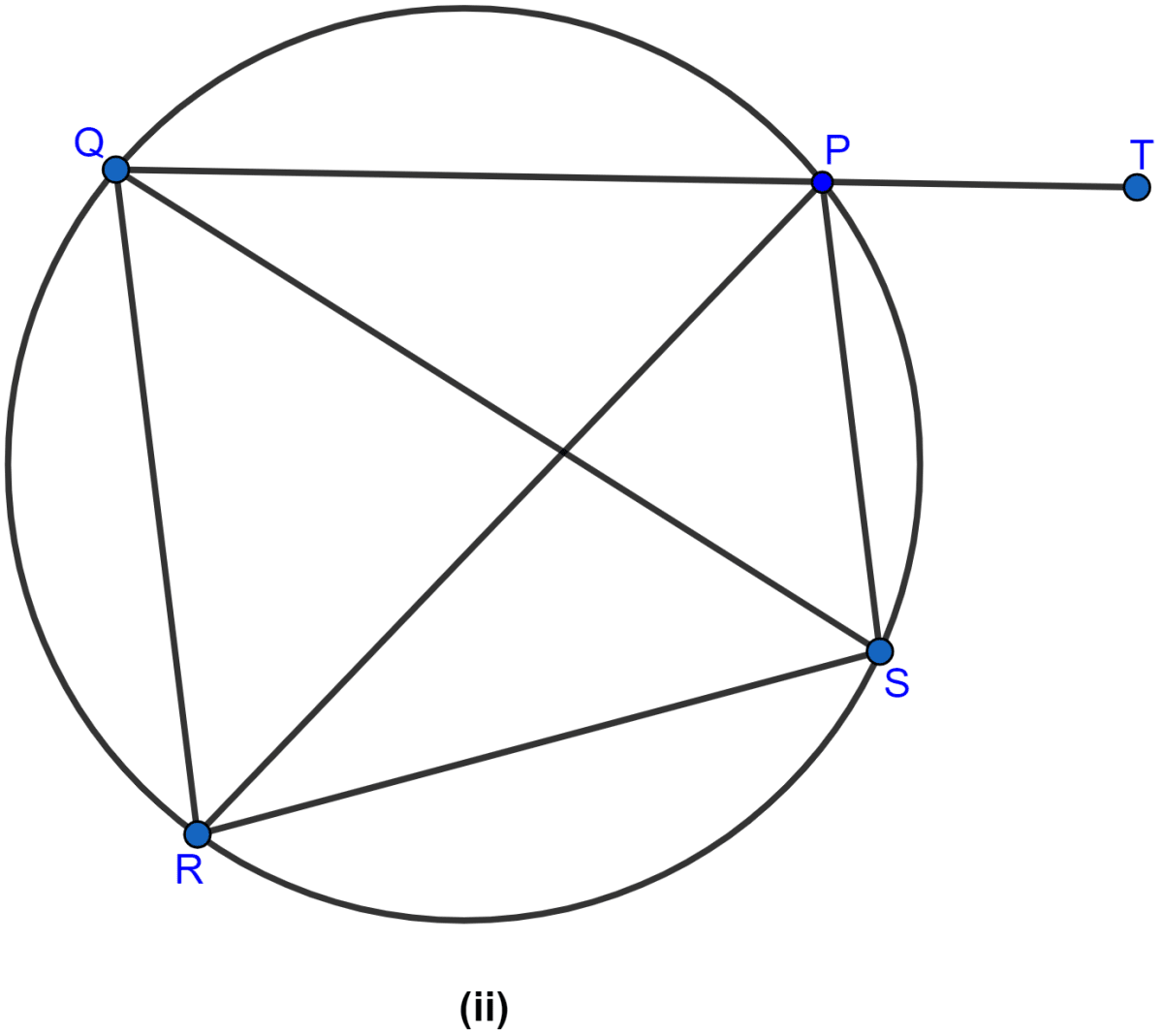
In the figure (ii) given below, SP is the bisector of ∠RPT and PQRS is a cyclic quadrilateral. Prove that SQ = RS.
Prove that a cyclic parallelogram is a rectangle.
Prove that a cyclic rhombus is a square.