Mathematics
Prove that a cyclic rhombus is a square.
Circles
66 Likes
Answer
Let ABCD be a cyclic rhombus.

In rhombus opposite angles are equal.
∴ ∠A = ∠C and ∠B = ∠D.
Sum of opposite angles of a cyclic quadrilateral is 180°
⇒ ∠A + ∠C = 180°
⇒ ∠A + ∠A = 180°
⇒ 2∠A = 180°
⇒ ∠A = 90°.
∴ ∠C = 90°.
Similarly,
⇒ ∠B + ∠D = 180°
⇒ ∠B + ∠B = 180°
⇒ 2∠B = 180°
⇒ ∠B = 90°.
∴ ∠D = 90°.
Hence, ∠A = ∠B = ∠C = ∠D = 90°.
In rhombus all sides are equal i.e. AD = BC = AB = CD.
Hence, ABCD is a square as all sides are equal and all the angles are equal to 90°.
Answered By
42 Likes
Related Questions
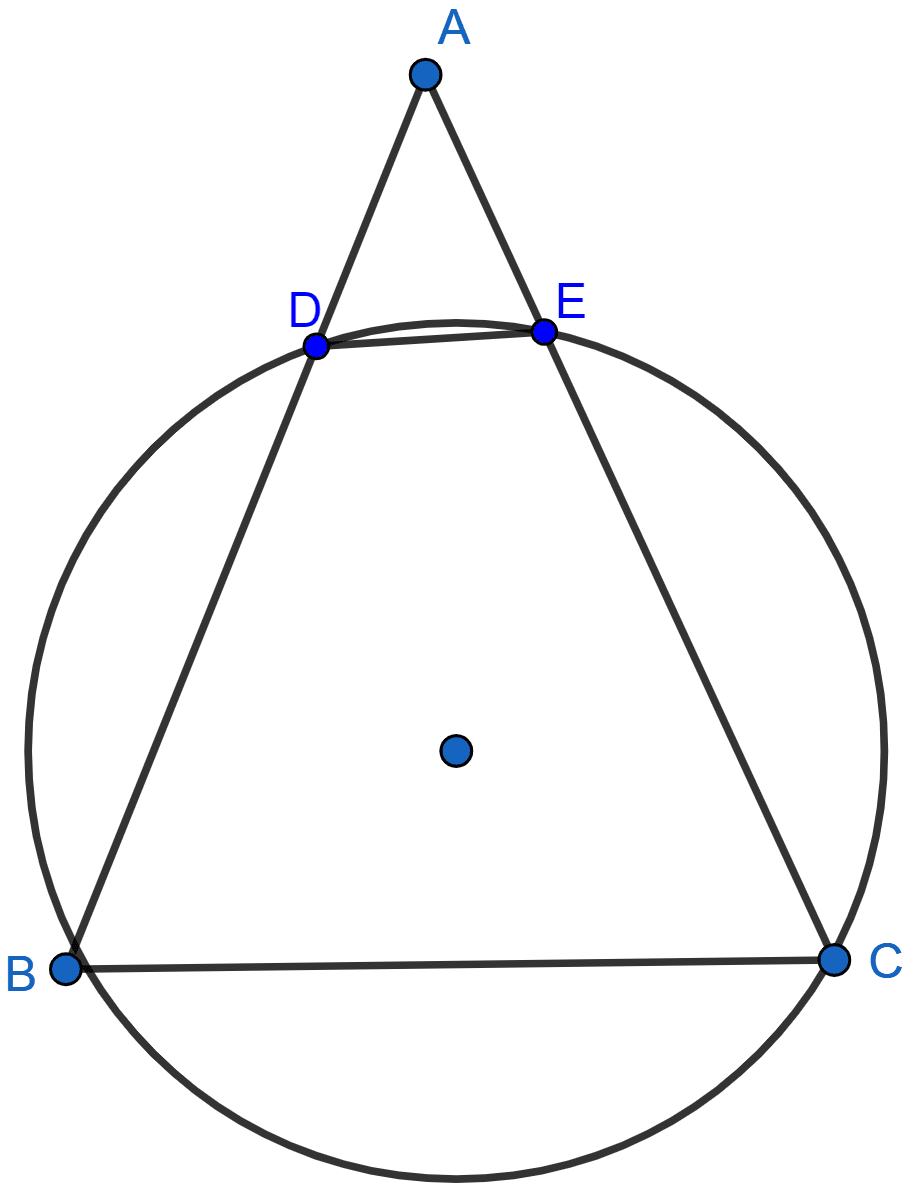
In the adjoining figure, ABC is an isosceles triangle in which AB = AC and circle passing through B and C intersects sides AB and AC at points D and E. Prove that DE || BC.
Prove that a cyclic parallelogram is a rectangle.
In the adjoining figure, chords AB and CD of the circle are produced to meet at O. Prove that triangles ODB and OAC are similar. Given that CD = 2 cm, DO = 6 cm and BO = 3 cm, calculate AB. Also find

Find the length of the tangent drawn to a circle of radius 3 cm, from a point distant 5 cm from the centre.