Mathematics
P is a point on bisector of angle A of △ABC. Then:
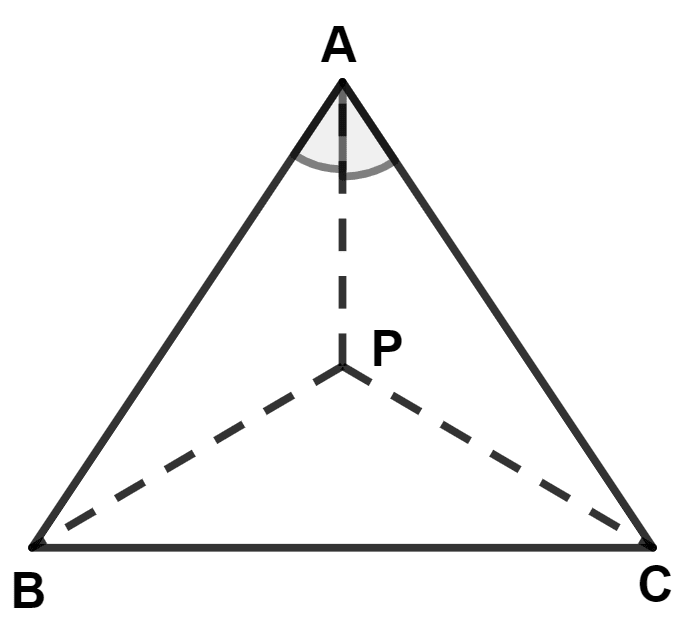
P is equidistant from the vertices B and C
PA = PC
PA = PB
P is equidistant from sides AB and AC of the △ABC.
Related Questions
Bisector of angle B of triangle ABC intersects side AC at point P, then point P is :
equidistant from vertices A and C
PA = PB
PB = PC
equidistant from sides AB and BC
The perpendicular bisector of side AB and bisector of angle A of △ABC meet at point P. Then :

PA = PB
PA = PC
PB = PC
PB bisects ∠ABC
P is a point on perpendicular bisector of side BC of △ABC, then :

PA = PB
PB = PC
PA = PC
none of these
Using the information in the given diagram, state if :

AD = DC
BD = DC
CD bisects angle ACB
angle CAD is greater than angle DAB