Mathematics
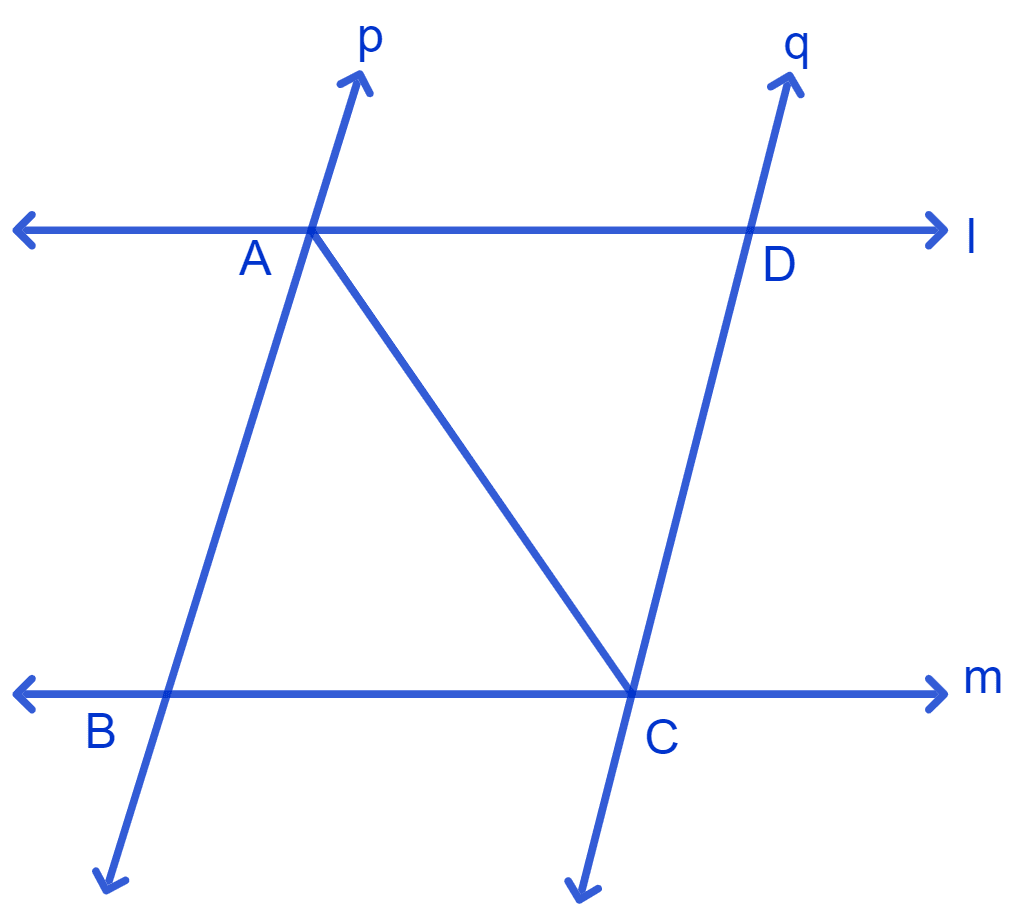
l and m are two parallel lines intersected by another pair of parallel lines p and q. Show that Δ ABC ≅ Δ CDA.
Triangles
14 Likes
Answer
Given :
l || m and p || q
In Δ ABC and Δ CDA,
⇒ ∠BAC = ∠DCA (Alternate interior angles are equal)
⇒ AC = CA (Common side)
⇒ ∠BCA = ∠DAC (Alternate interior angles are equal)
∴ Δ ABC ≅ Δ CDA (By A.S.A. congruence rule)
Hence, proved that Δ ABC ≅ Δ CDA.
Answered By
8 Likes
Related Questions
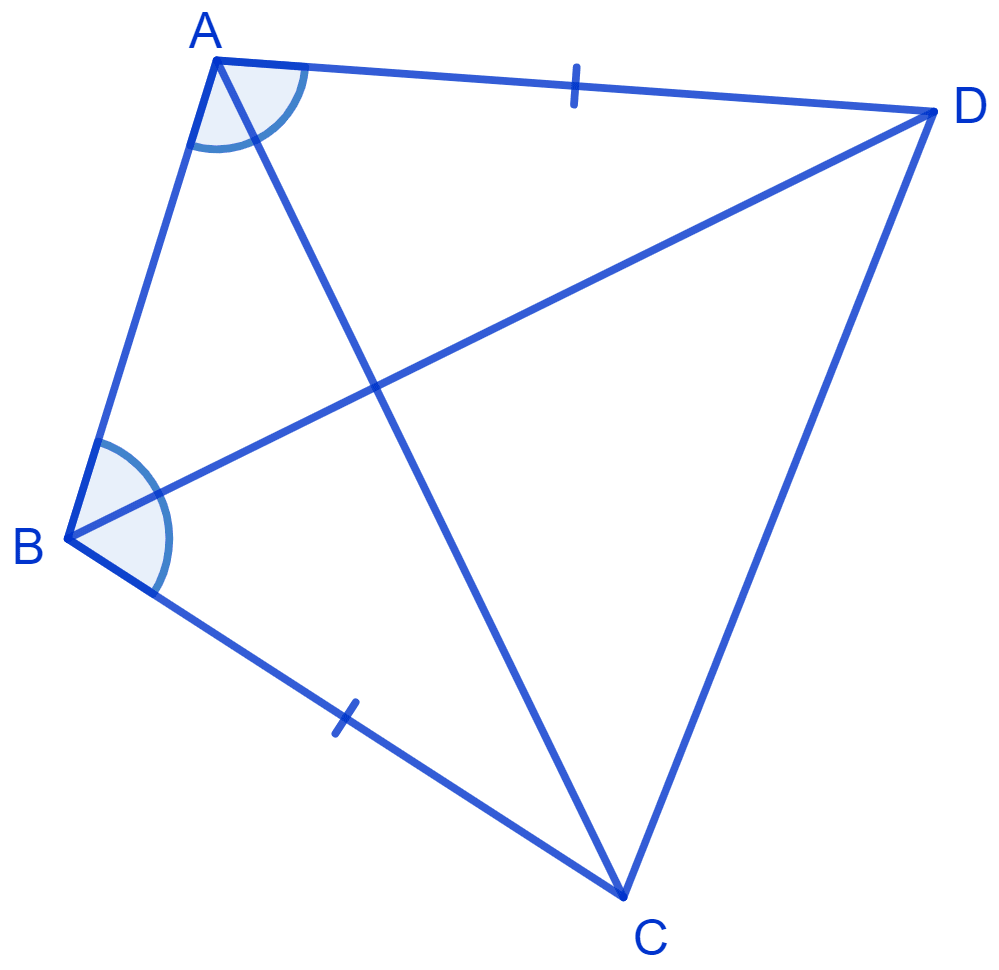
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA. Prove that
(i) Δ ABD ≅ Δ BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC
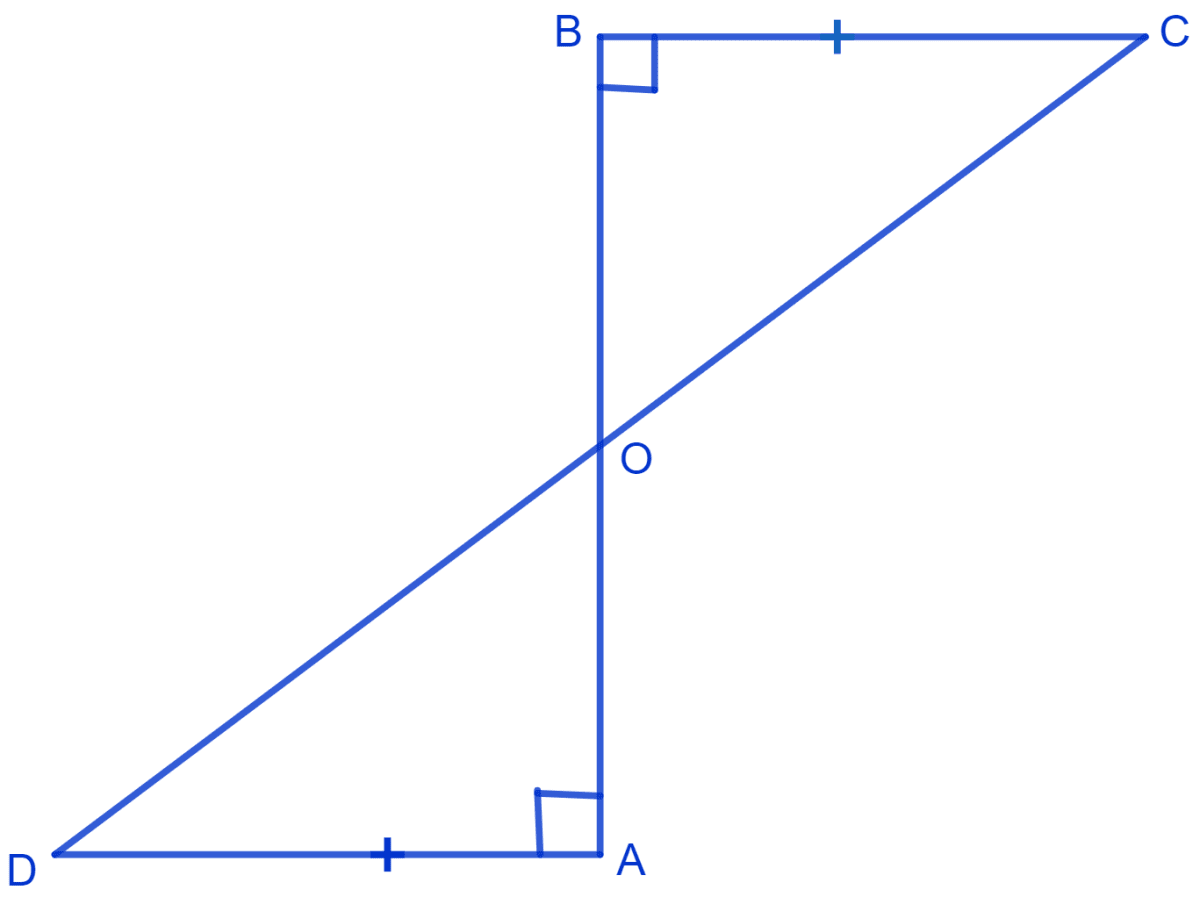
AD and BC are equal, perpendiculars to a line segment AB. Show that CD bisects AB.
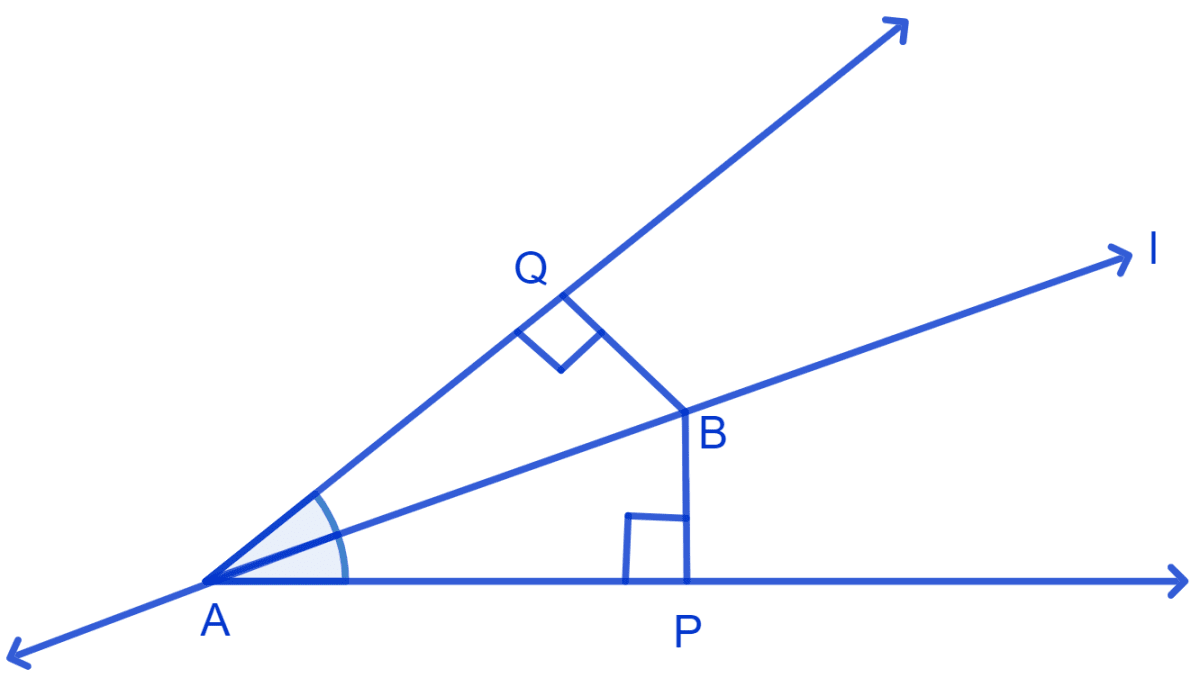
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A. Show that:
(i) Δ APB ≅ Δ AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.
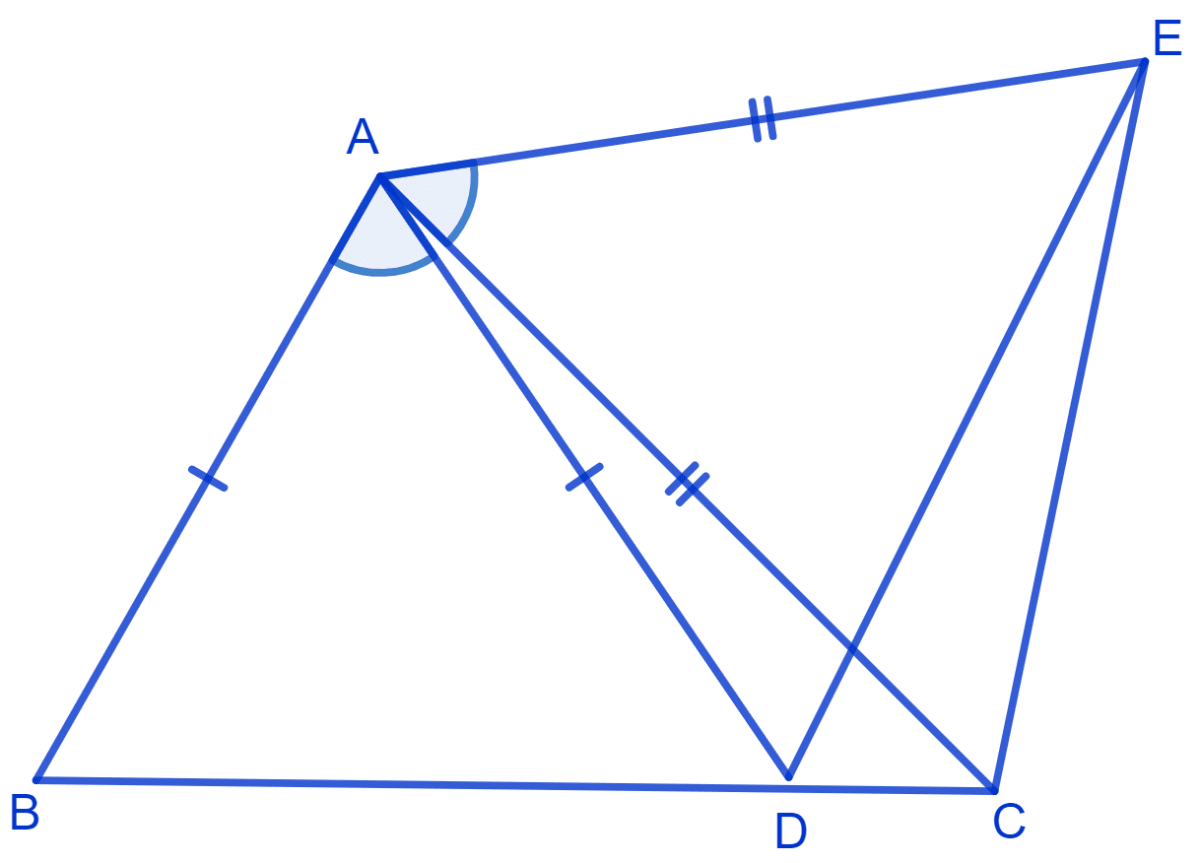
In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.