Mathematics
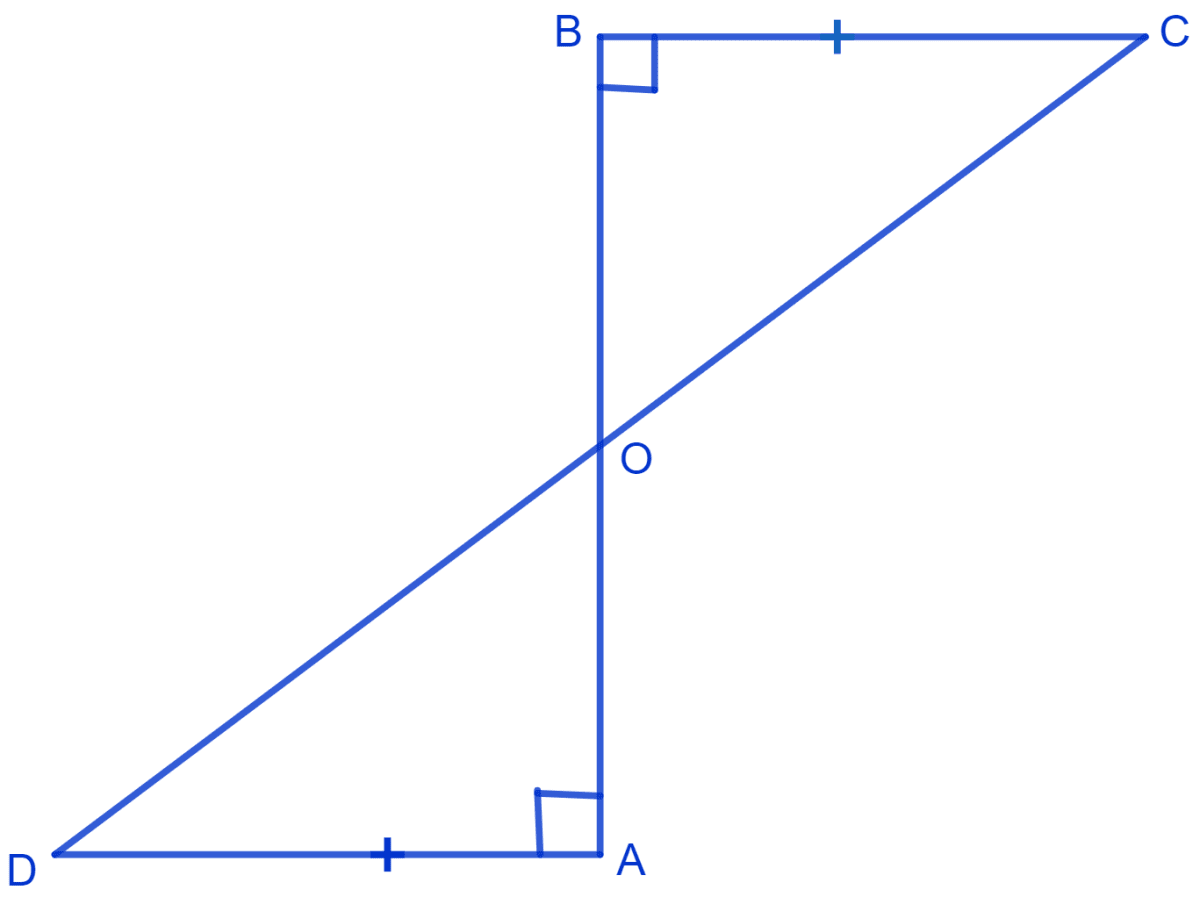
AD and BC are equal, perpendiculars to a line segment AB. Show that CD bisects AB.
Triangles
4 Likes
Answer
Given :
⇒ AD = BC
From figure,
⇒ AD ⊥ AB, ∠OAD = 90°
⇒ BC ⊥ AB, ∠OBC = 90°
In △ BOC and △ AOD,
⇒ ∠BOC = ∠AOD (Vertically opposite angles are equal)
⇒ ∠OBC = ∠OAD (Each equal to 90°)
⇒ BC = AD (Given)
∴ △ BOC ≅ △ AOD (By A.A.S. congruence rule)
We know that,
Corresponding parts of congruent triangles are equal.
∴ BO = AO (By C.P.C.T.)
Hence, proved that CD bisects AB and O is the mid-point of AB.
Answered By
2 Likes
Related Questions
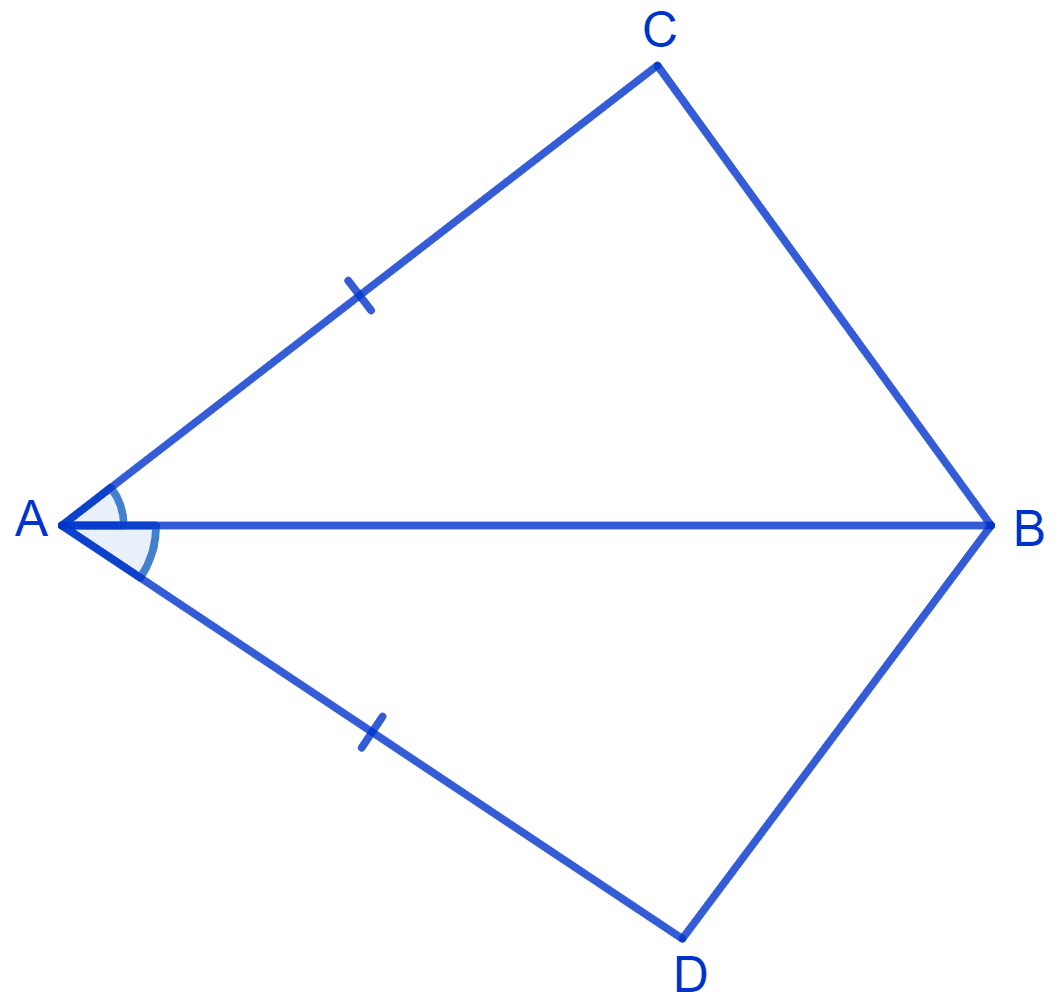
In quadrilateral ACBD, AC = AD and AB bisects ∠A. Show that Δ ABC ≅ Δ ABD. What can you say about BC and BD?
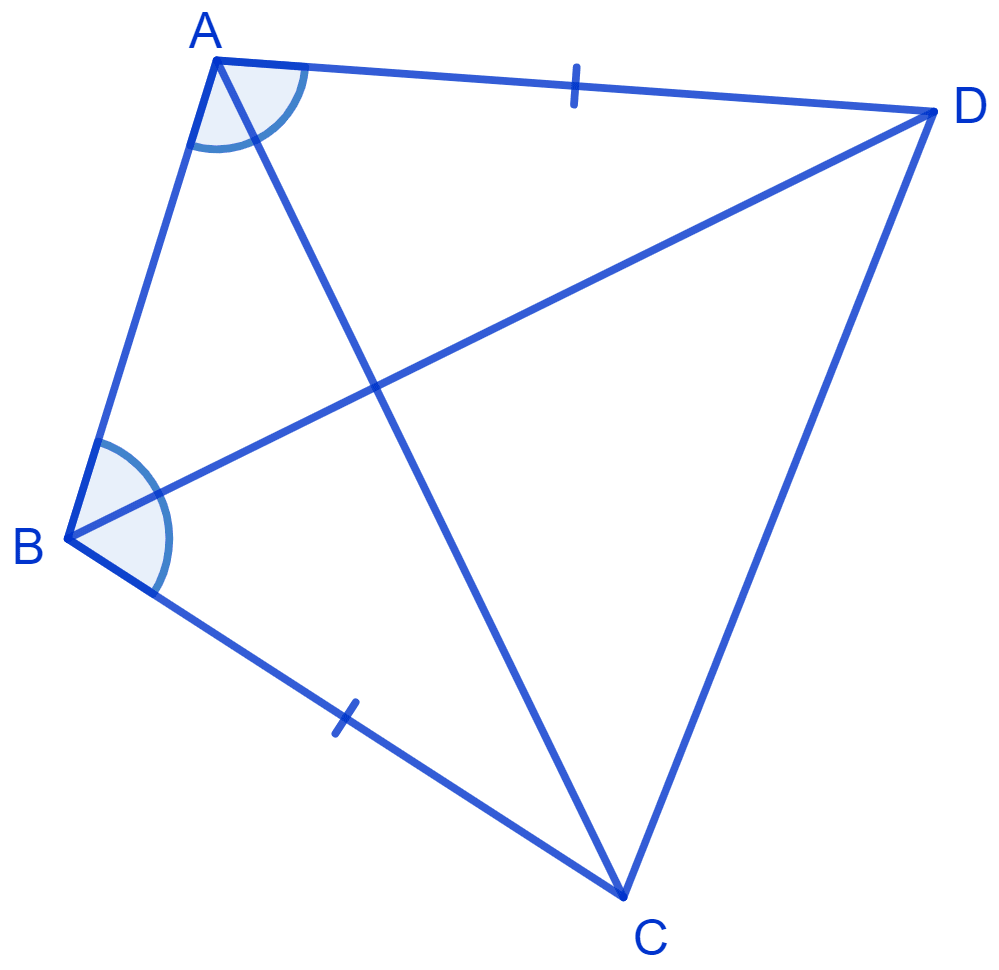
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA. Prove that
(i) Δ ABD ≅ Δ BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC
l and m are two parallel lines intersected by another pair of parallel lines p and q. Show that Δ ABC ≅ Δ CDA.
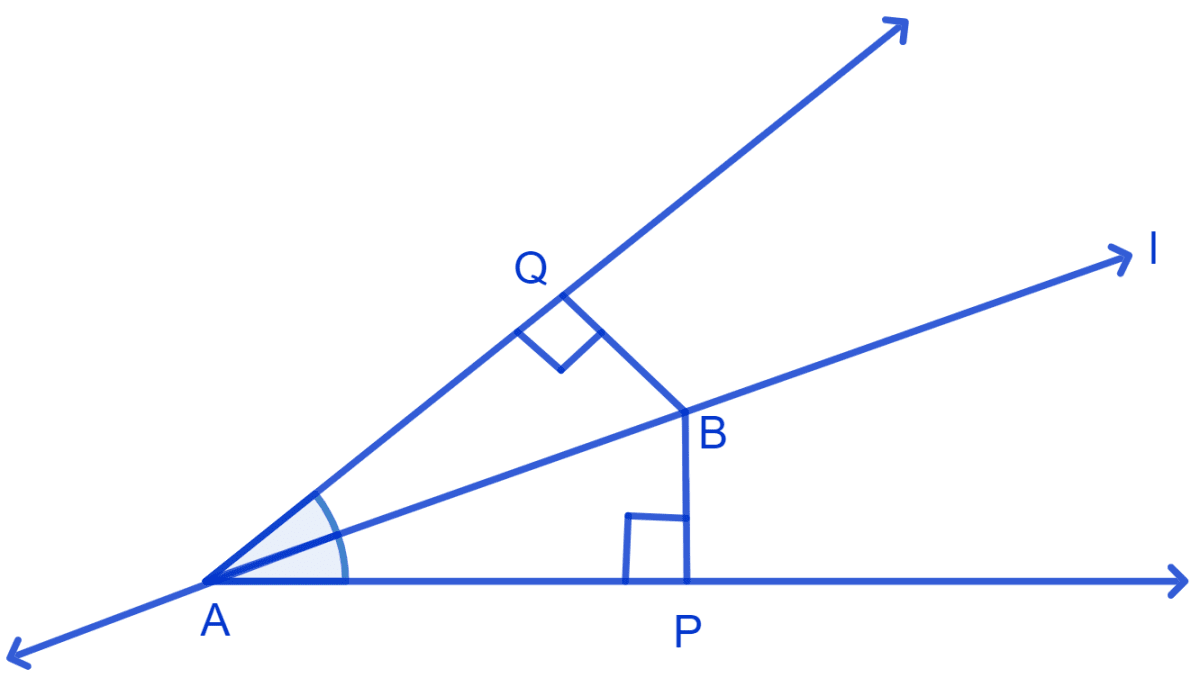
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A. Show that:
(i) Δ APB ≅ Δ AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.