Mathematics
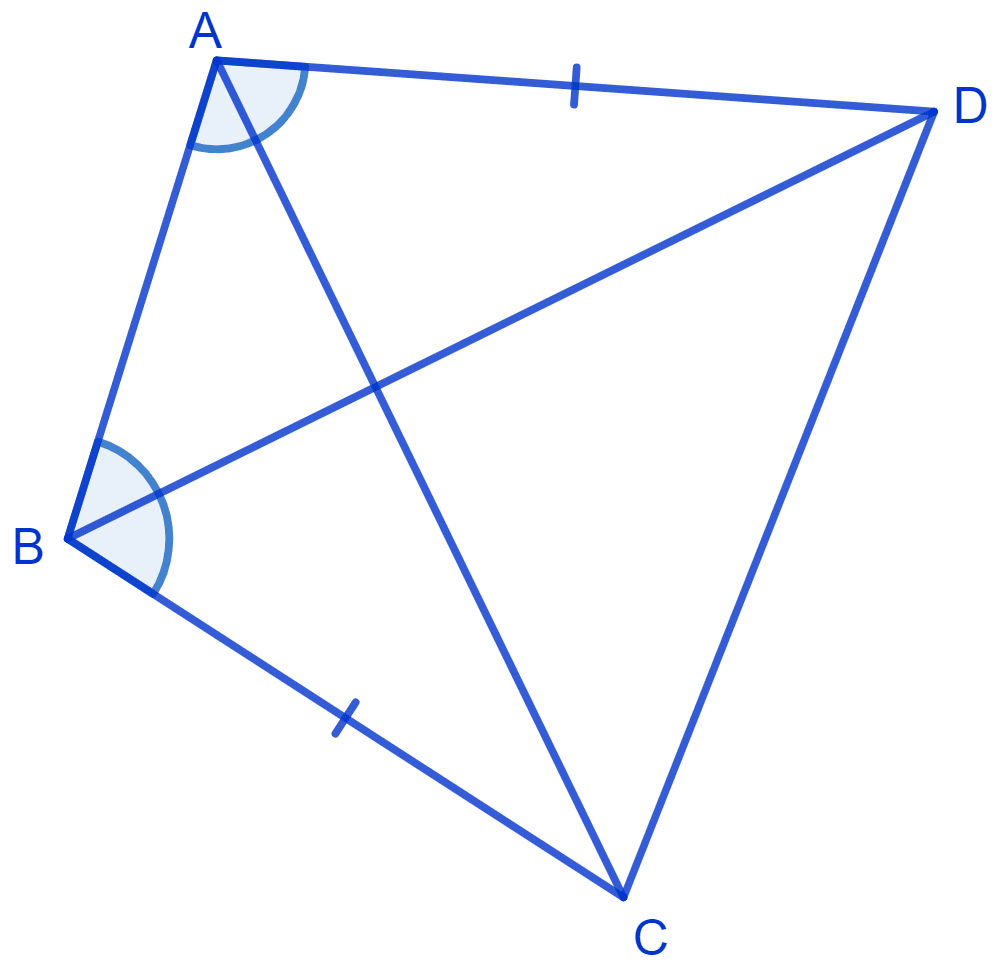
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA. Prove that
(i) Δ ABD ≅ Δ BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC
Triangles
6 Likes
Answer
Given :
AD = BC and ∠DAB = ∠CBA
(i) In △ ABD and △ BAC,
⇒ AD = BC (Given)
⇒ ∠DAB = ∠CBA (Given)
⇒ AB = BA (Common side)
∴ △ ABD ≅ △ BAC (By S.A.S. congruence rule)
Hence, proved that △ ABD ≅ △ BAC.
(ii) As,
△ ABD ≅ △ BAC,
We know that,
Corresponding parts of congruent triangles are equal.
∴ BD = AC (By C.P.C.T.)
Hence, proved that BD = AC.
(iii) As,
△ ABD ≅ △ BAC,
We know that,
Corresponding parts of congruent triangles are equal.
⇒ ∠ABD = ∠BAC (By C.P.C.T.)
Hence, proved that ∠ABD = ∠BAC.
Answered By
3 Likes
Related Questions
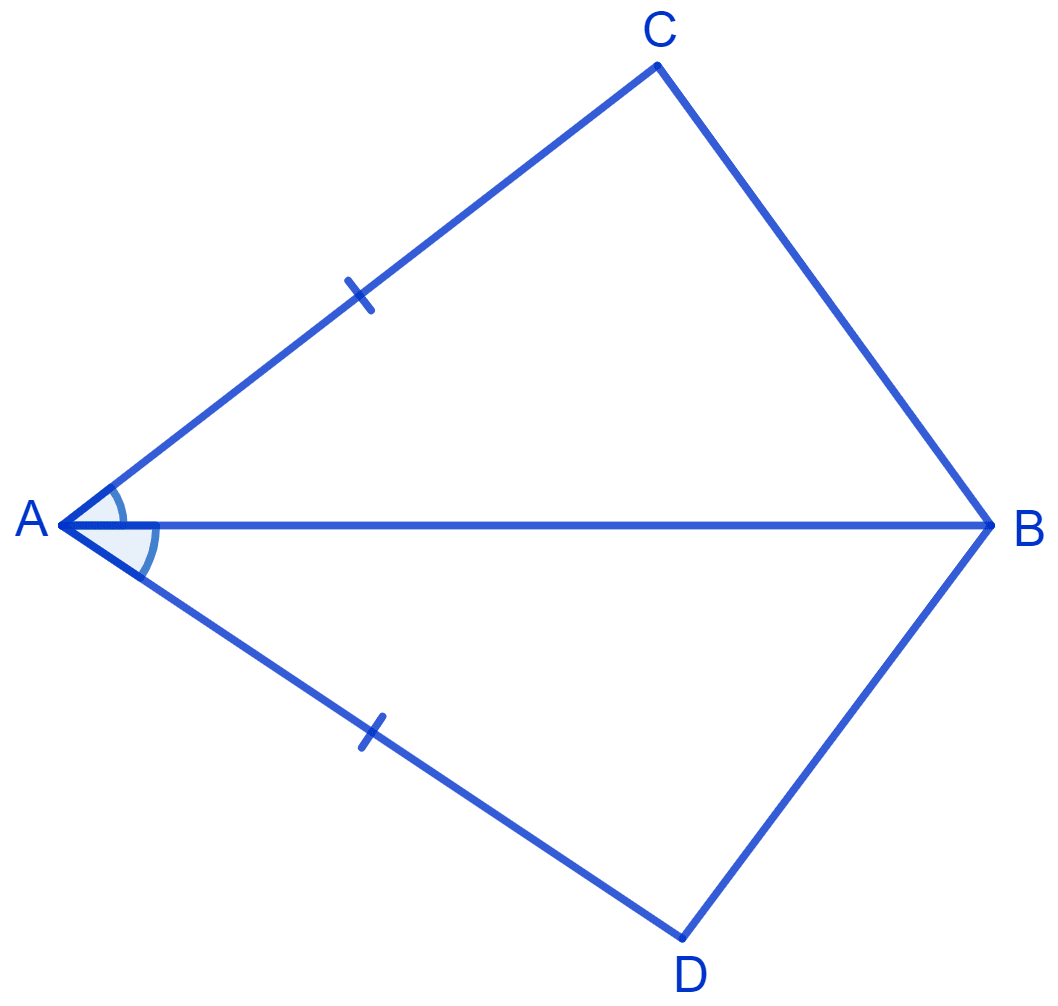
In quadrilateral ACBD, AC = AD and AB bisects ∠A. Show that Δ ABC ≅ Δ ABD. What can you say about BC and BD?
AD and BC are equal, perpendiculars to a line segment AB. Show that CD bisects AB.
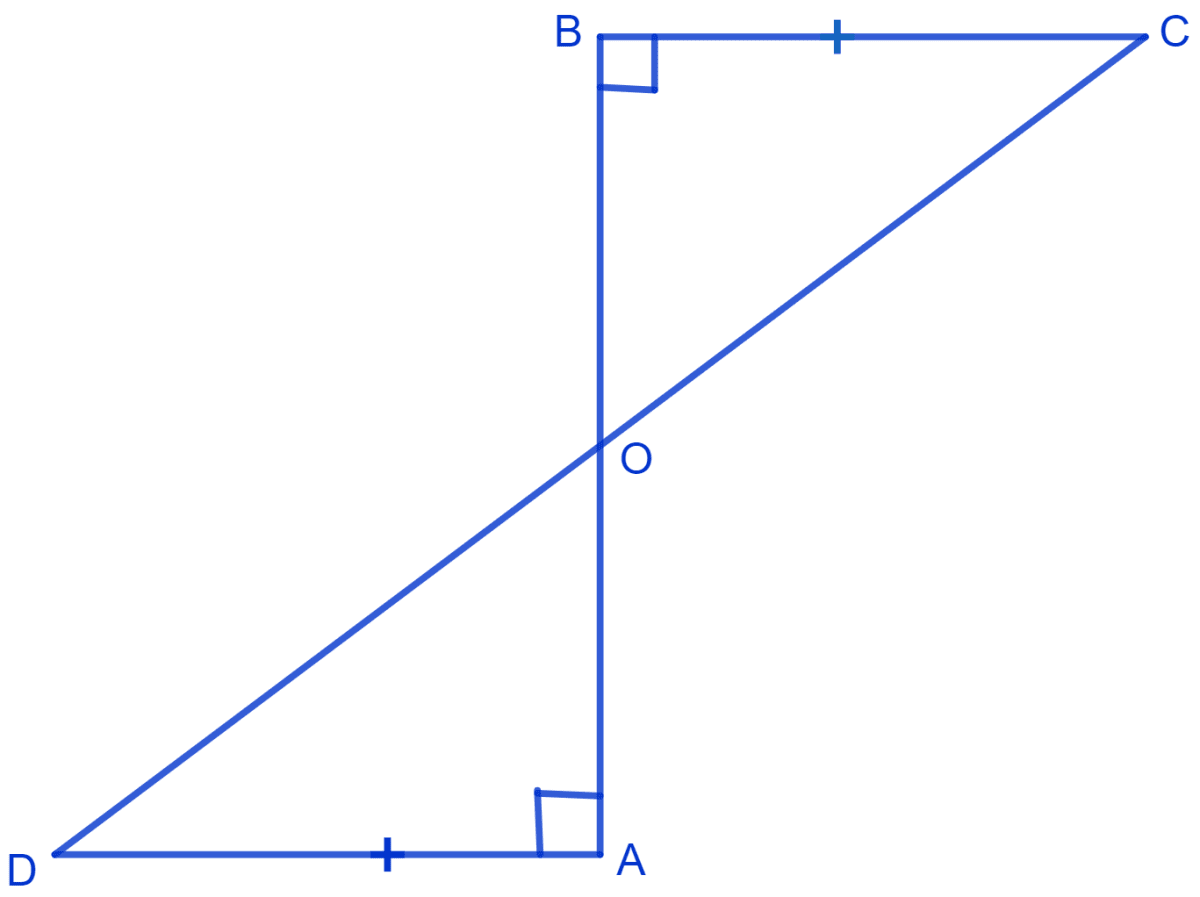
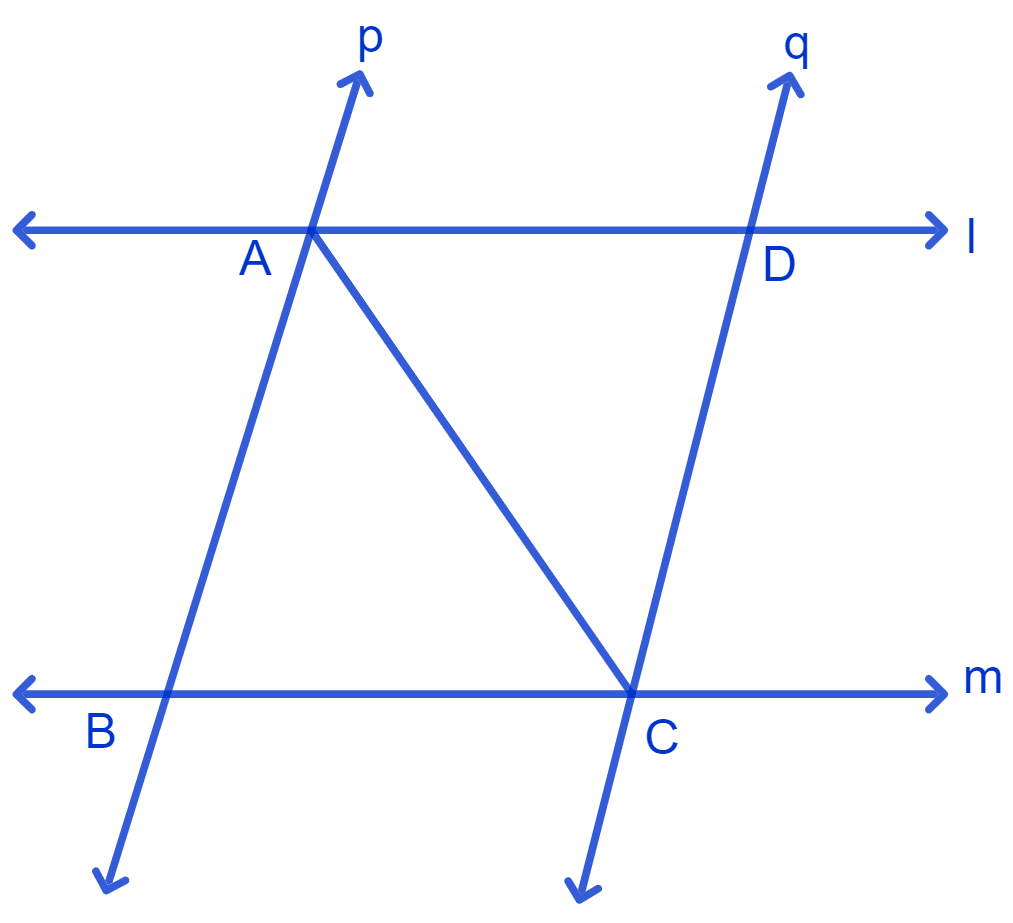
l and m are two parallel lines intersected by another pair of parallel lines p and q. Show that Δ ABC ≅ Δ CDA.
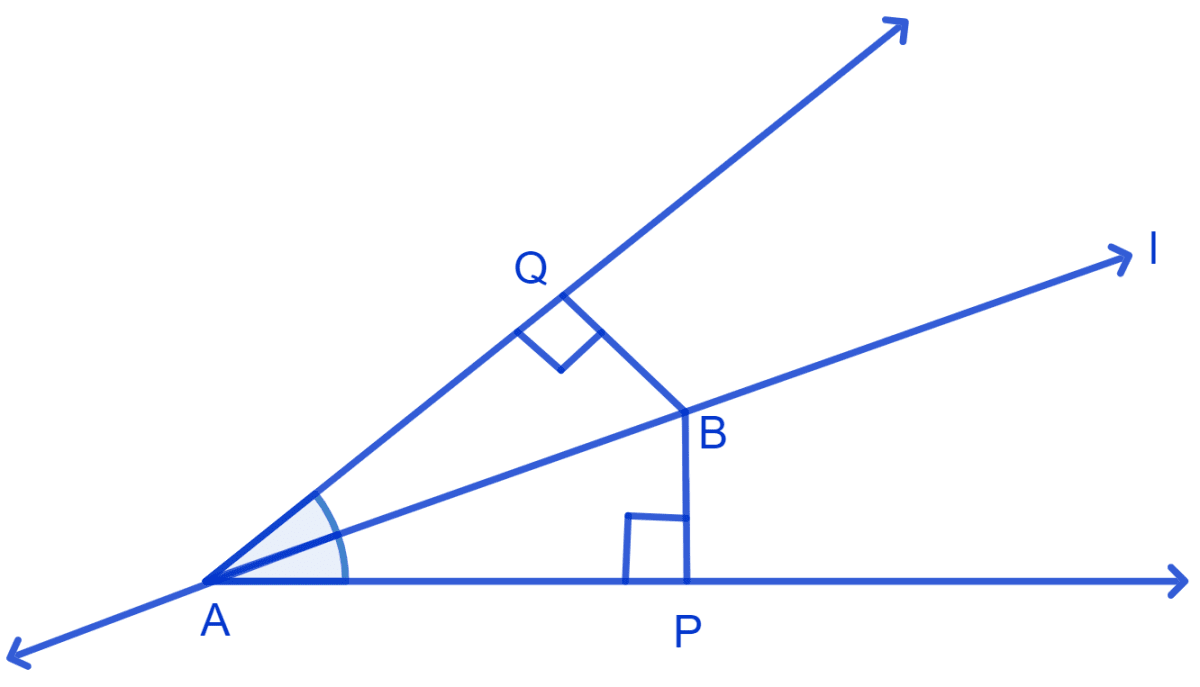
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A. Show that:
(i) Δ APB ≅ Δ AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.