Mathematics
It is given that △ABC ≅ △RPQ. Is it true to say that BC = QR? Why?
Triangles
90 Likes
Answer
Given, △ABC ≅ △RPQ.
It means that A ↔ R, B ↔ P, C ↔ Q, therefore, BC = PQ (corresponding sides are equal).
Hence, BC ≠ QR as they are not corresponding sides.
Answered By
59 Likes
Related Questions
"If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent." Is the statement true? Why?
In the adjoining figure, AD = BC and BD = AC. Prove that:
∠ADB = ∠BCA and ∠DAB = ∠CBA.
In the adjoining figure, AB = AC, P and Q are points on BA and CA respectively such that AP = AQ. Prove that
(i) △APC ≅ △AQB
(ii) CP = BQ
(iii) ∠ACP = ∠ABQ.
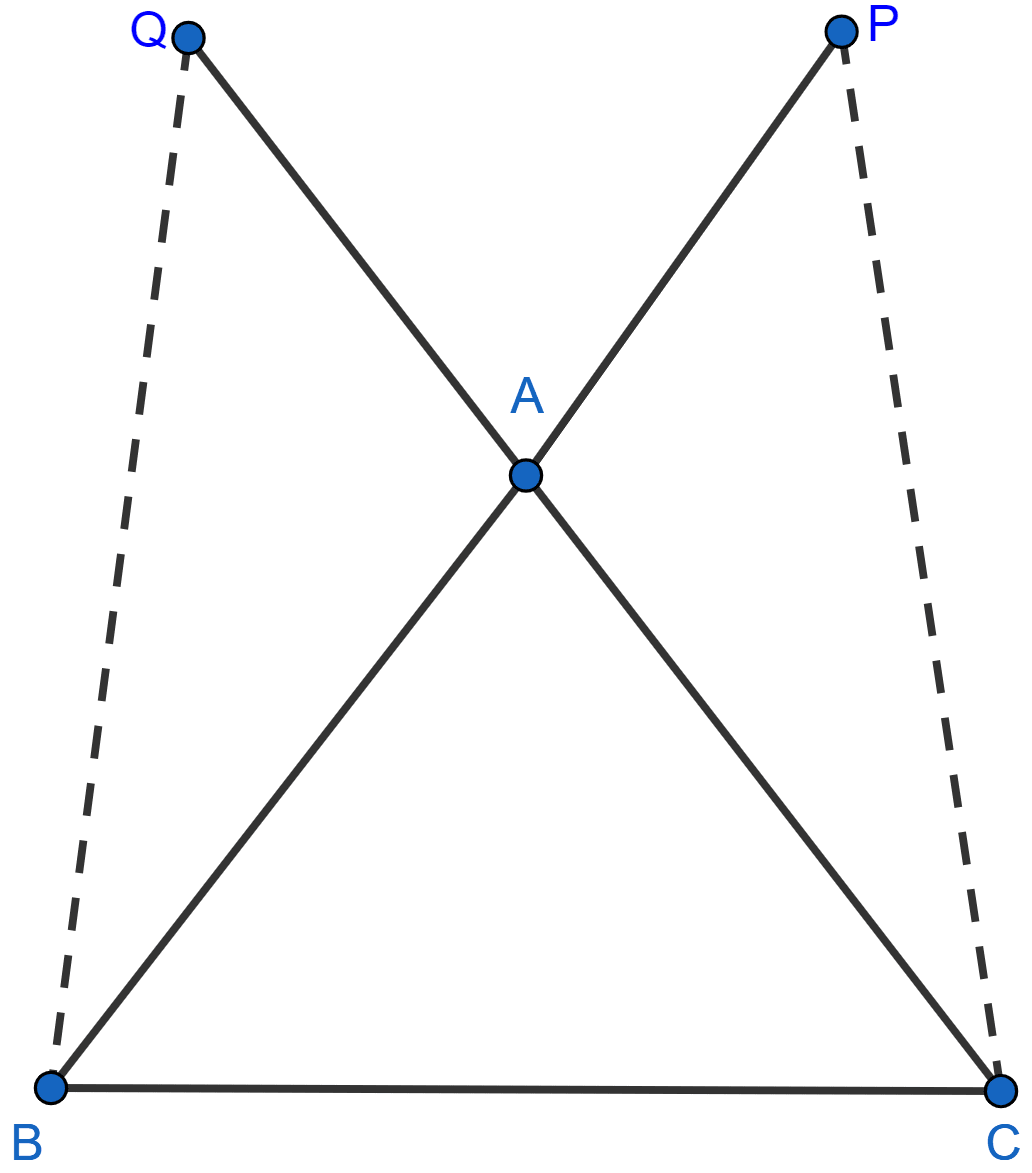
In the adjoining figure, AB = AC and AP = AQ. Prove that
(i) △APC ≅ △AQB
(ii) CP = BQ
(iii) ∠APC = ∠AQB.
