Mathematics
In triangle ABC, D is mid-point of AB and CD is perpendicular to AB. Bisector of ∠ABC meets CD at E and AC at F. Prove that :
(i) E is equidistant from A and B.
(ii) F is equidistant from AB and BC.
Answer
(i) Join AE.
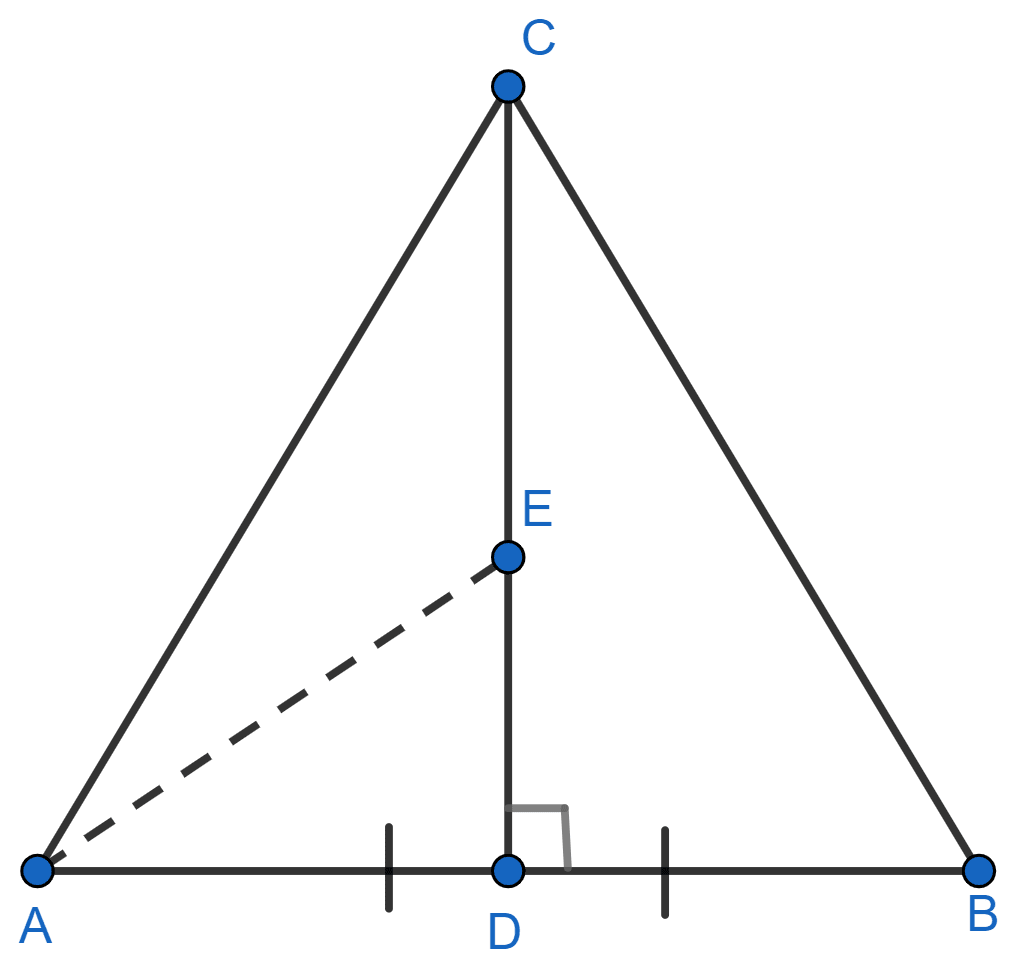
In △EAD and △EBD,
⇒ ED = ED (Common)
⇒ AD = BD (As D is the mid-point of AB)
⇒ ∠EDA = ∠EDB (Both = 90°).
∴ △EAD ≅ △EBD (By SAS axiom)
∴ EA = EB (By C.P.C.T.)
Hence, proved that E is equidistant from A and B.
(ii) Draw FL ⊥ BC and FM ⊥ AB.
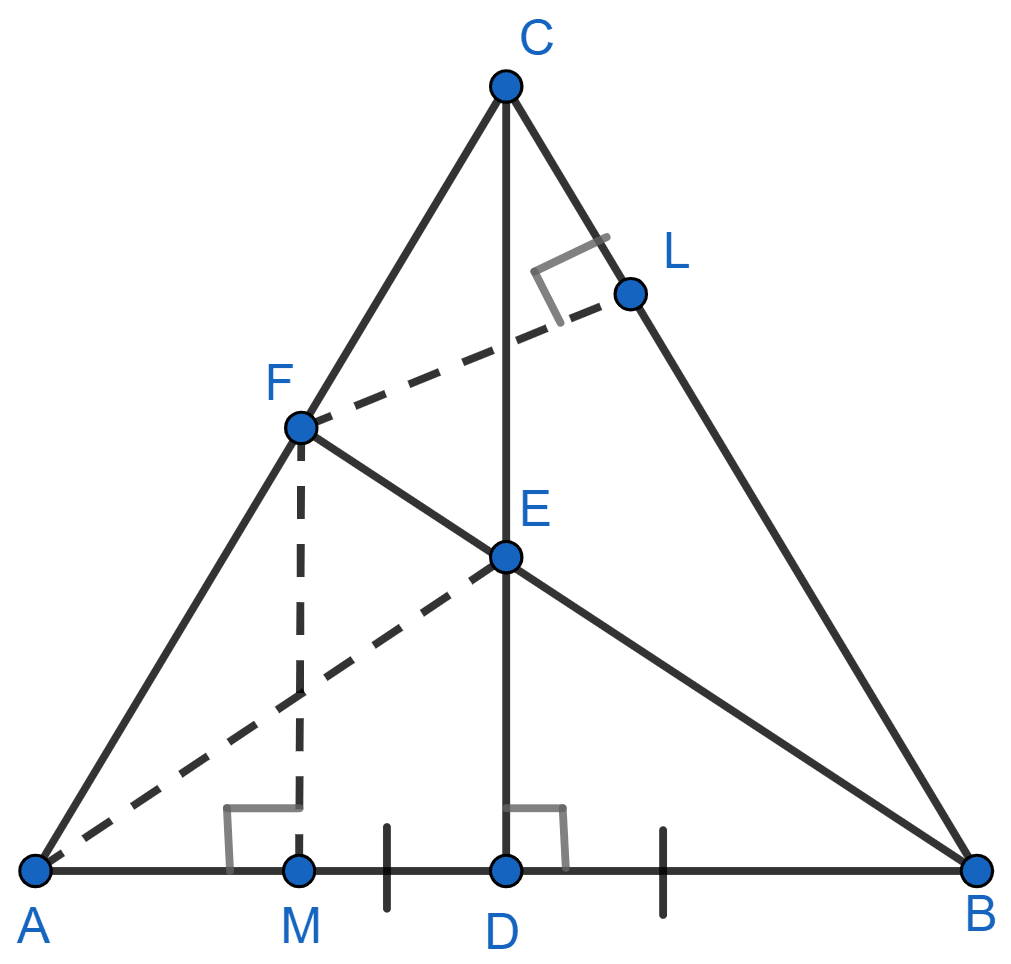
In △BLF and △BMF,
⇒ BF = BF (Common)
⇒ ∠LBF = ∠FBM (As BF is the angle bisector of ∠ABC)
⇒ ∠BLF = ∠BMF (Both = 90°).
∴ △BLF ≅ △BMF (By ASA axiom)
∴ FL = FM (By C.P.C.T.)
Hence, proved that F is equidistant from AB and BC.
Related Questions
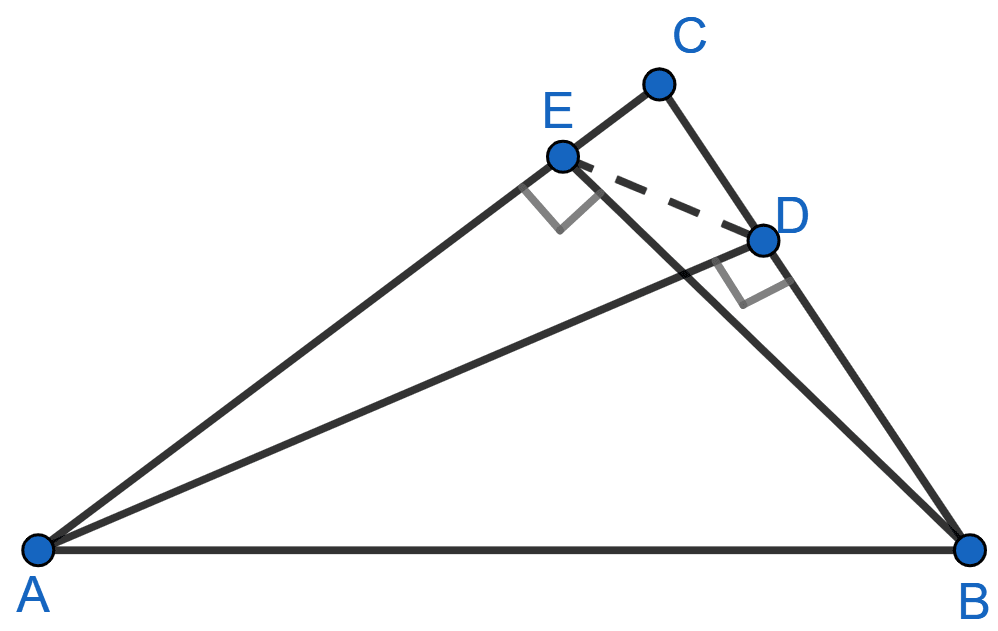
The following figure shows a triangle ABC in which AD and BE are perpendiculars to BC and AC respectively.
Show that :
(i) △ADC ~ △BEC
(ii) CA × CE = CB × CD
(iii) △ABC ~ △DEC
(iv) CD × AB = CA × DE
Use graph paper for this question. Take 2 cm = 1 unit on both axes.
(i) Plot the points A(1, 1), B(5, 3) and C(2, 7).
(ii) Construct the locus of points equidistant from A and B.
(iii) Construct the locus of points equidistant from AB and AC.
(iv) Locate the point P such that PA = PB and P is equidistant from AB and AC.
(v) Measure and record the length PA in cm.
The speed of sound is 332 meters per second. A gun is fired. Describe the locus of all the people on the earth's surface, who hear the sound exactly one second later.