Mathematics
In the given figure, PQ is a diameter. Chord SR is parallel to PQ. Given that ∠PQR = 58°, Calculate :
(i) ∠RPQ
(ii) ∠STP.

Answer
Join PR.

(i) ∠PRQ = 90° [Angle in semi-circle is a right angle.]
In △PQR,
⇒ ∠RPQ + ∠PRQ + ∠PQR = 180° [Angle sum property of triangle]
⇒ ∠RPQ + 90° + 58° = 180°
⇒ ∠RPQ + 148° = 180°
⇒ ∠RPQ = 180° - 148° = 32°.
Hence, ∠RPQ = 32°.
(ii) As, SR || PQ,
∠PRS = ∠RPQ = 32° [Alternate angles are equal]
In cyclic quadrilateral PRST,
⇒ ∠STP + ∠PRS = 180° [As sum of opposite angles in a cyclic quadrilateral = 180°]
⇒ ∠STP = 180° - ∠PRS = 180° - 32° = 148°.
Hence, ∠STP = 148°.
Related Questions
In the given figure, AOC is a diameter and AC is parallel to ED. If ∠CBE = 64°, calculate ∠DEC.

Use the given figure to find :
(i) ∠BAD
(ii) ∠DQB.

AB is the diameter of the circle with center O. OD is parallel to BC and ∠AOD = 60°. Calculate the numerical values of :
(i) ∠ABD,
(ii) ∠DBC,
(iii) ∠ADC.
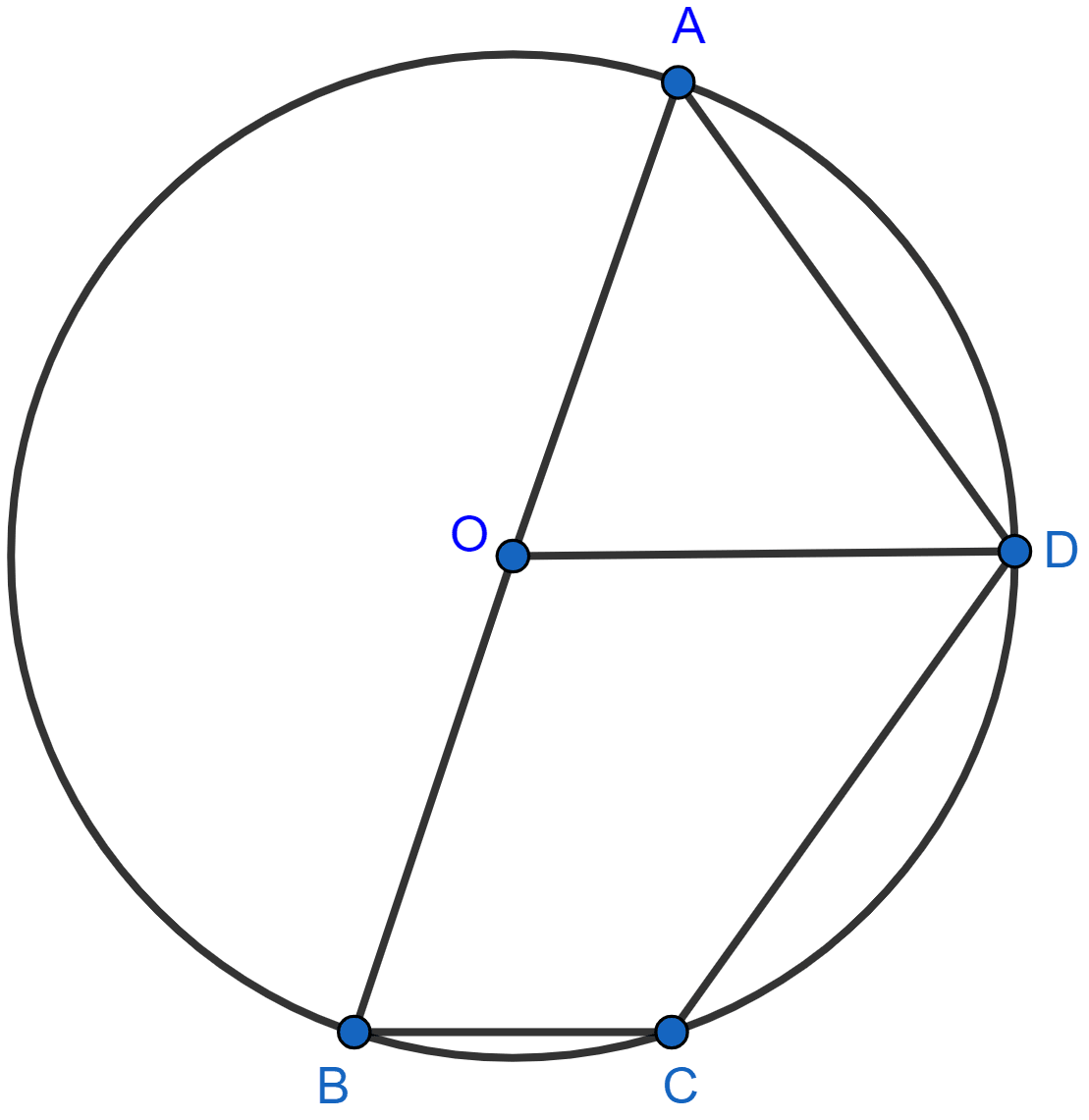
In the given figure, the center O of the small circle lies on the circumference of the bigger circle. If ∠APB = 75° and ∠BCD = 40°, find :
(i) ∠AOB,
(ii) ∠ACB,
(iii) ∠ABD,
(iv) ∠ADB.