Mathematics
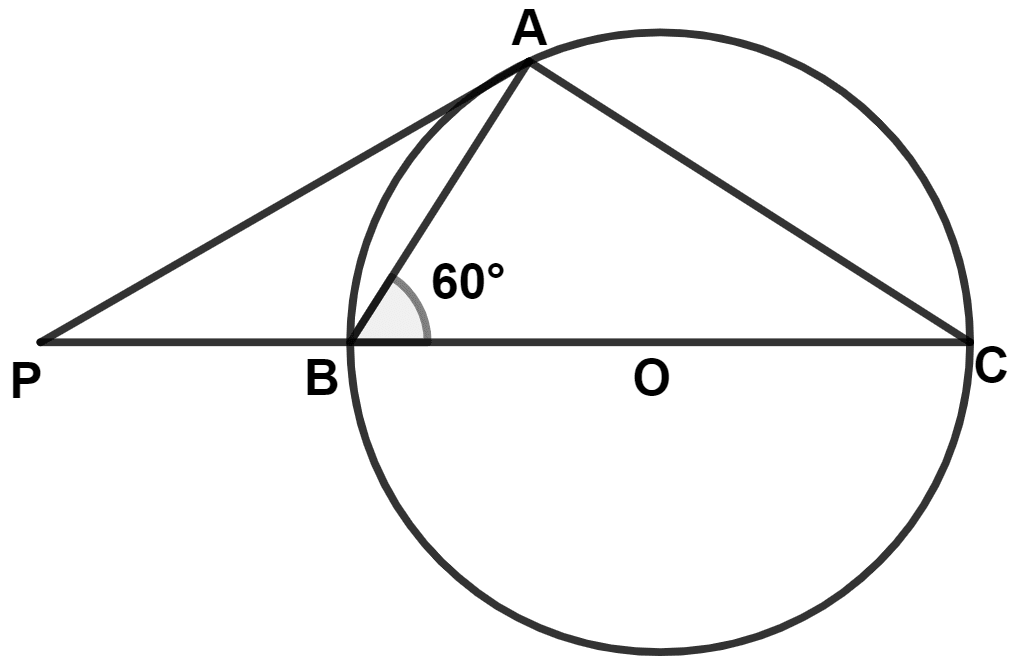
In the given figure, O is the center of the circle, PA is tangent and PBC is secant. If ∠ABC = 60°; ∠P is :
30°
60°
120°
90°
Answer
In △ABC,
∠BAC = 90° (Angle in semi-circle is a right angle)
⇒ ∠ABC + ∠BAC + ∠ACB = 180° (By angle sum property of triangle)
⇒ 60° + 90° + ∠ACB = 180°
⇒ 150° + ∠ACB = 180°
⇒ ∠ACB = 180° - 150° = 30°.
We know that,
The angle between a tangent and a chord through the point of contact is equal to an angle in the alternate segment.
⇒ ∠BAP = ∠ACB = 30°.
From figure,
⇒ ∠PBA + ∠ABC = 180° [Linear pairs]
⇒ ∠PBA + 60° = 180°
⇒ ∠PBA = 180° - 60° = 120°.
In △PBA,
⇒ ∠PBA + ∠BAP + ∠APB = 180° (By angle sum property of triangle)
⇒ 120° + 30° + ∠APB = 180°
⇒ 150° + ∠APB = 180°
⇒ ∠APB = 180° - 150° = 30°.
∴ ∠P = 30°.
Hence, Option 1 is the correct option.
Related Questions
In the given circle, PA is tangent and PBC is secant, PA = 8 cm and PB = 4 cm. The length of BC is :
8 cm
12 cm
16 cm
2 cm

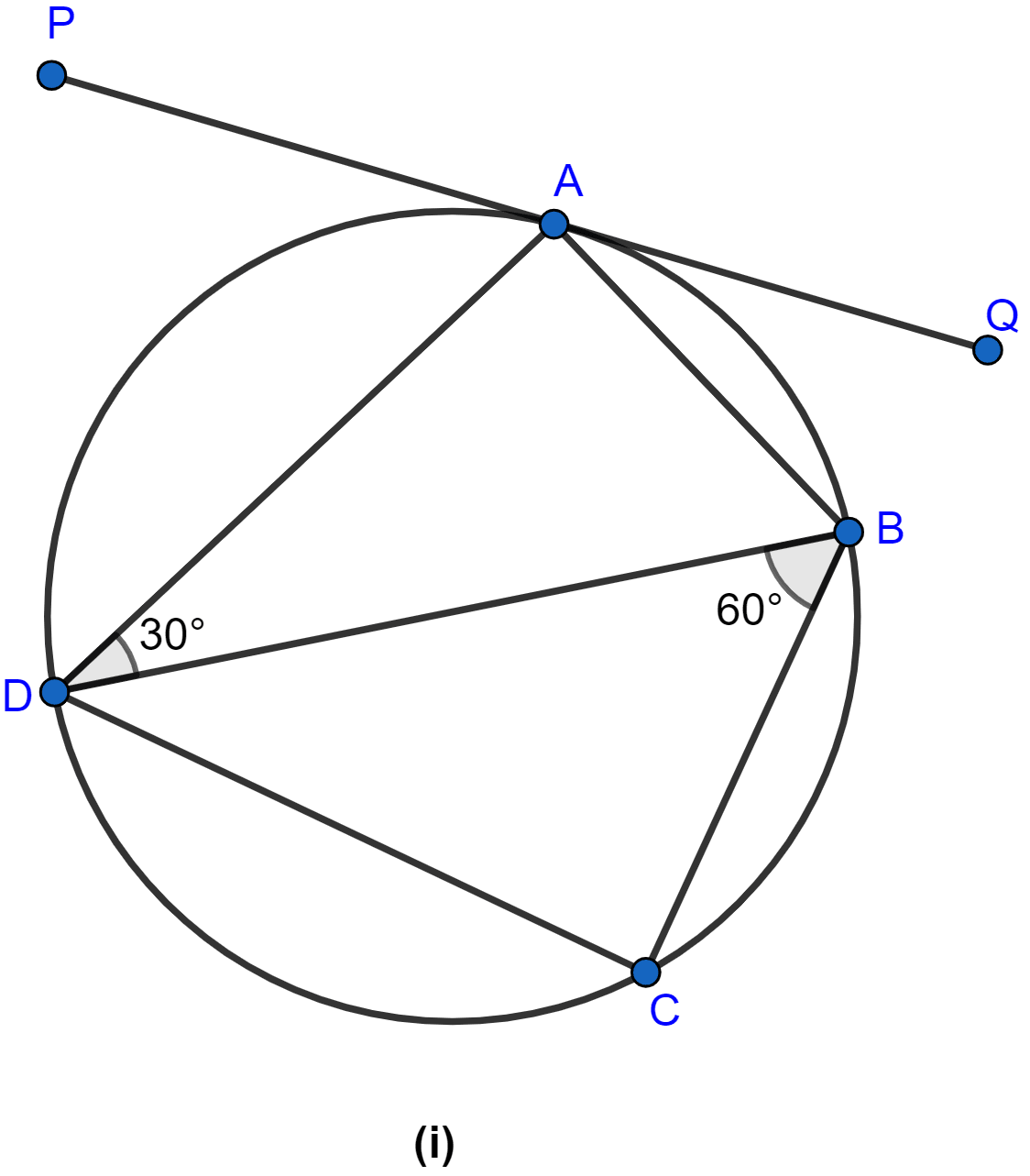
In the figure (i) given below, PQ is a tangent to the circle at A, DB is a diameter, ∠ADB = 30° and ∠CBD = 60°, calculate
(i) ∠QAB
(ii) ∠PAD
(iii) ∠CDB.
AC is a tangent to the given circle which touches the circle at point B. If ∠EBC = 45°; angle EDB is equal to :
45°
90°
125°
135°

In the given figure, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find :
(i) AB
(ii) the length of tangent PT.