Mathematics
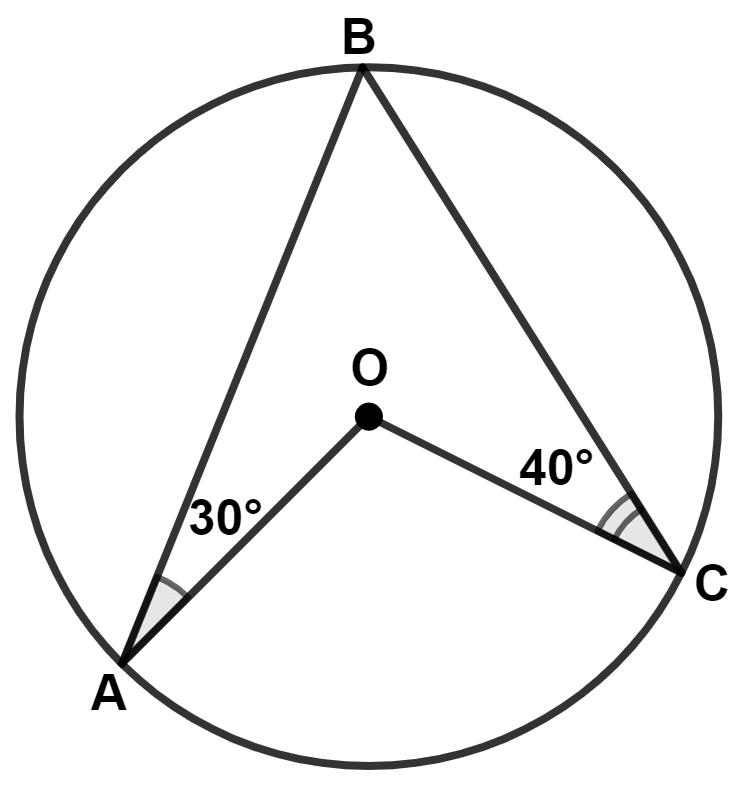
In the given figure, O is the center of the circle. ∠OAB and ∠OCB are 30° and 40° respectively. ∠AOC is equal to :
70°
80°
150°
140°
Circles
7 Likes
Answer
Join AC.
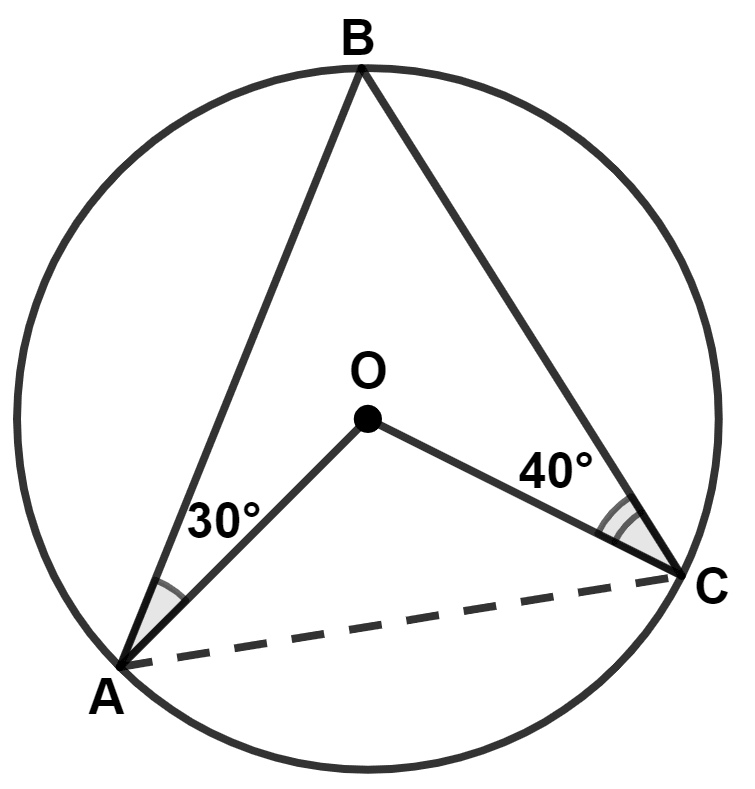
In △AOC,
Since,
OA = OC (Radius of same circle)
∴ ∠OAC = ∠OCA = x (let)
By angle sum property of triangle,
⇒ ∠OAC + ∠OCA + ∠AOC = 180°
⇒ x + x + ∠AOC = 180°
⇒ ∠AOC = 180° - 2x
In △AOC,
By angle sum property of triangle,
⇒ ∠BAC + ∠ACB + ∠CBA = 180°
⇒ (30° + x) + (40° + x) + ∠CBA = 180°
⇒ ∠CBA + 70° + 2x = 180°
⇒ ∠CBA = 180° - 70° - 2x
⇒ ∠CBA = 110° - 2x
We know that,
The angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.
∴ ∠AOC = 2∠CBA
⇒ 180° - 2x = 2(110° - 2x)
⇒ 180° - 2x = 220° - 4x
⇒ 4x - 2x = 220° - 180°
⇒ 2x = 40°
⇒ x = = 20°.
⇒ ∠AOC = 180° - 2x
⇒ ∠AOC = 180° - 2(20°) = 180° - 40° = 140°.
Hence, Option 4 is the correct option.
Answered By
4 Likes
Related Questions
ABCD is a trapezium with AD parallel to BC. Side BC is produced to point E and angle DCE = 95°. Angle B is equal to :
85°
105°
95°
175°

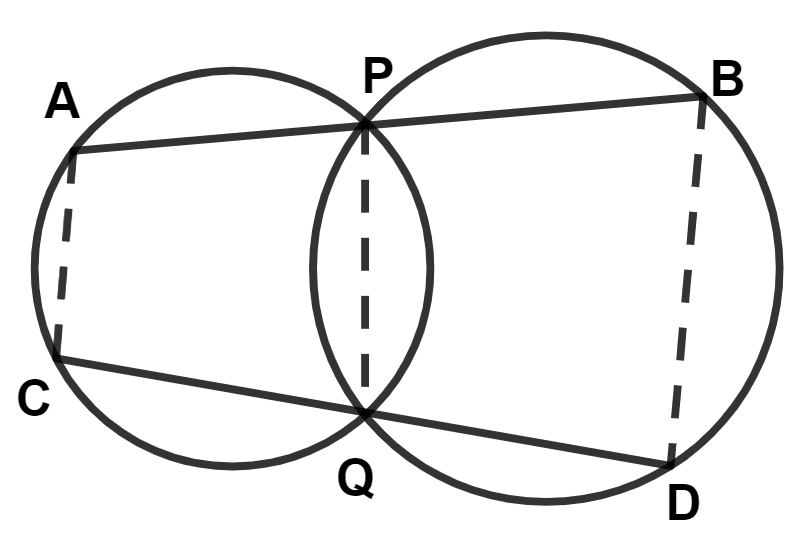
In the given figure APB and CQD are two straight lines, then :
AB || CD
AC || PQ
PQ || BD
AC || BD
In the figure, given below, ∠ABC is equal to :
105°
75°
90°
45°

In the given figure, ABC is an equilateral triangle. Angle ADC is :
60°
100°
80°
120°
