Mathematics
In the given figure, O is the center of the circle. If chord AB = chord AC, OP ⊥ AB and OQ ⊥ AC; show that : PB = QC.
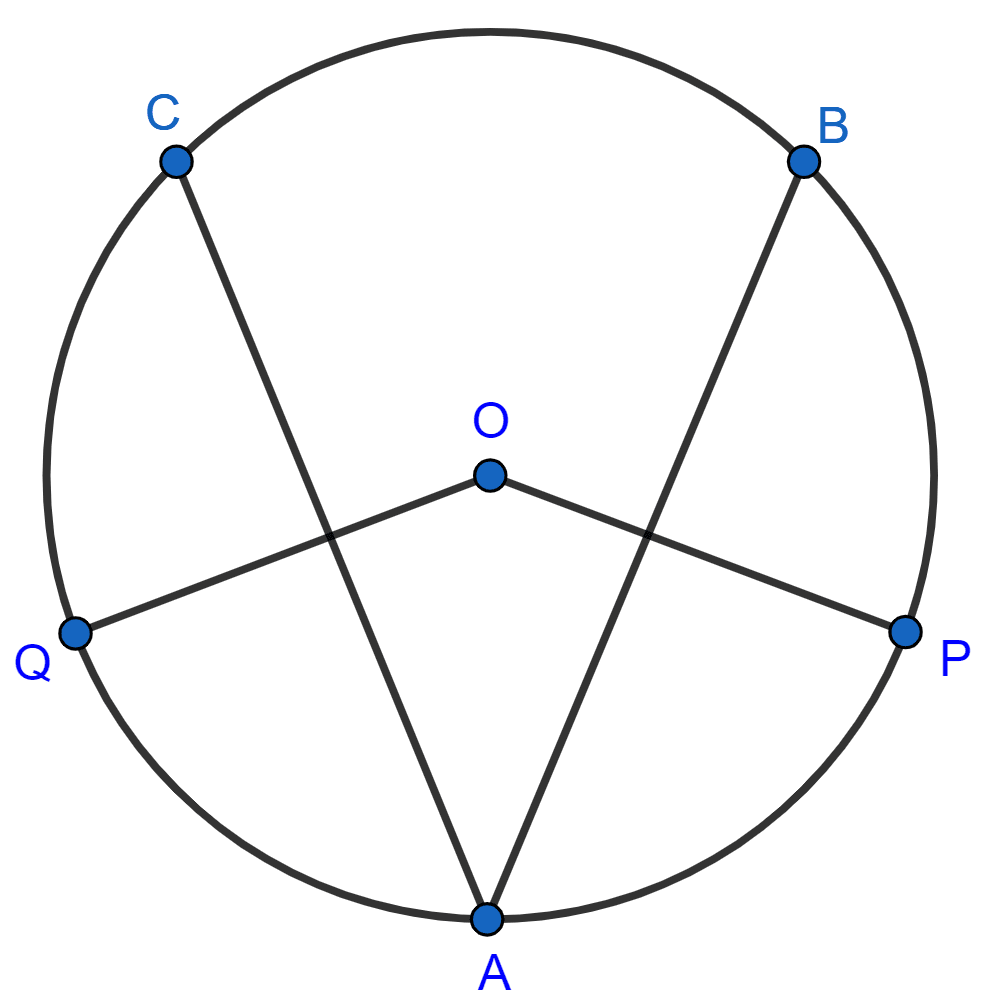
Circles
9 Likes
Answer
Let AB = AC = x
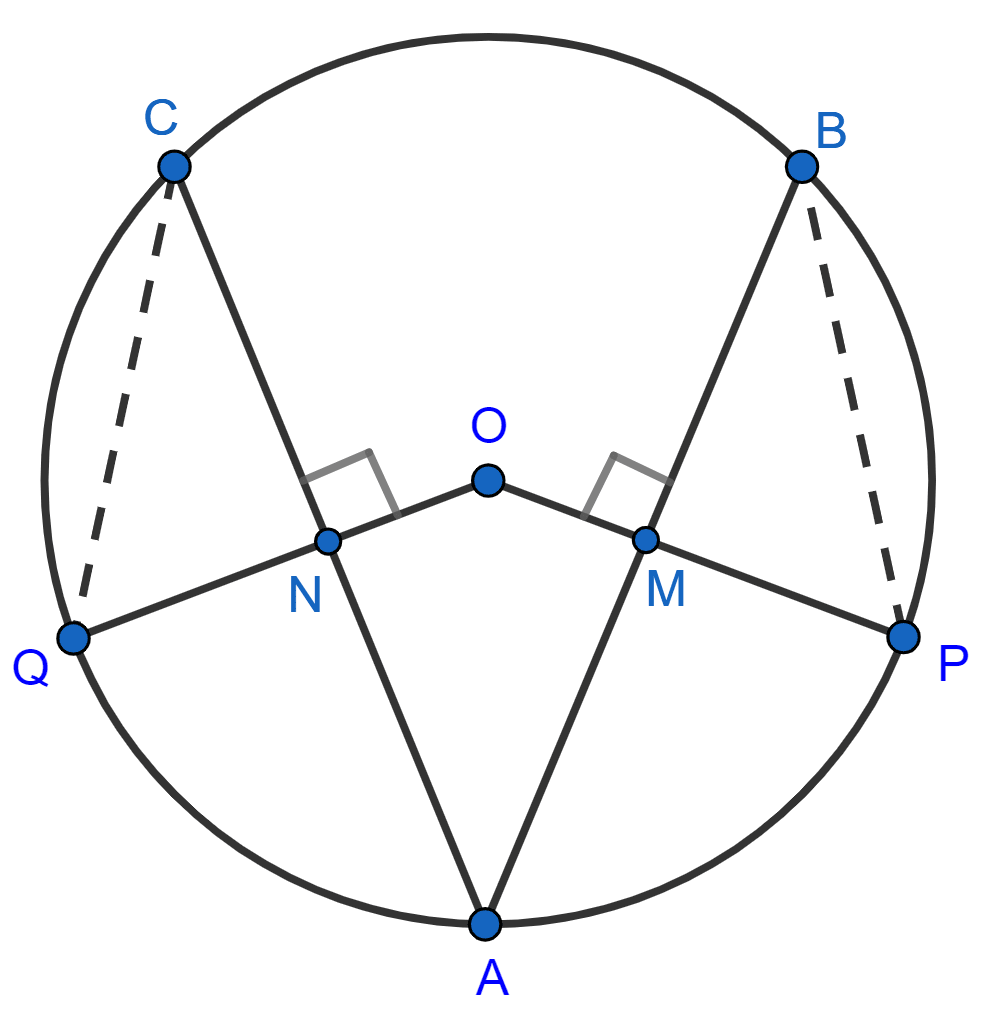
Given,
OP ⊥ AB and OQ ⊥ AC
⇒ OM ⊥ AB and ON ⊥ AC
Since, the perpendicular to a chord from the center of the circle bisects the chord,
∴ AM = MB = and AN = NC =
∴ MB = NC ………….(1)
Since, equal chords of a circle are equidistant from the center,
∴ ON = OM = y (let)
Let radius of circle be r.
From figure,
⇒ OQ = OP = r
⇒ QN = OQ - ON = r - y
⇒ PM = OP - OM = r - y
∴ QN = PM ………(2)
In △QNC and △PMB,
⇒ NC = MB [From (1)]
⇒ QN = PM [From (2)]
⇒ ∠QNC = ∠PMB [Both equal to 90°]
∴ △QNC ≅ △∠PMB by SAS axiom.
∴ PB = QC (By C.P.C.T.)
Hence, proved that PB = QC.
Answered By
4 Likes
Related Questions
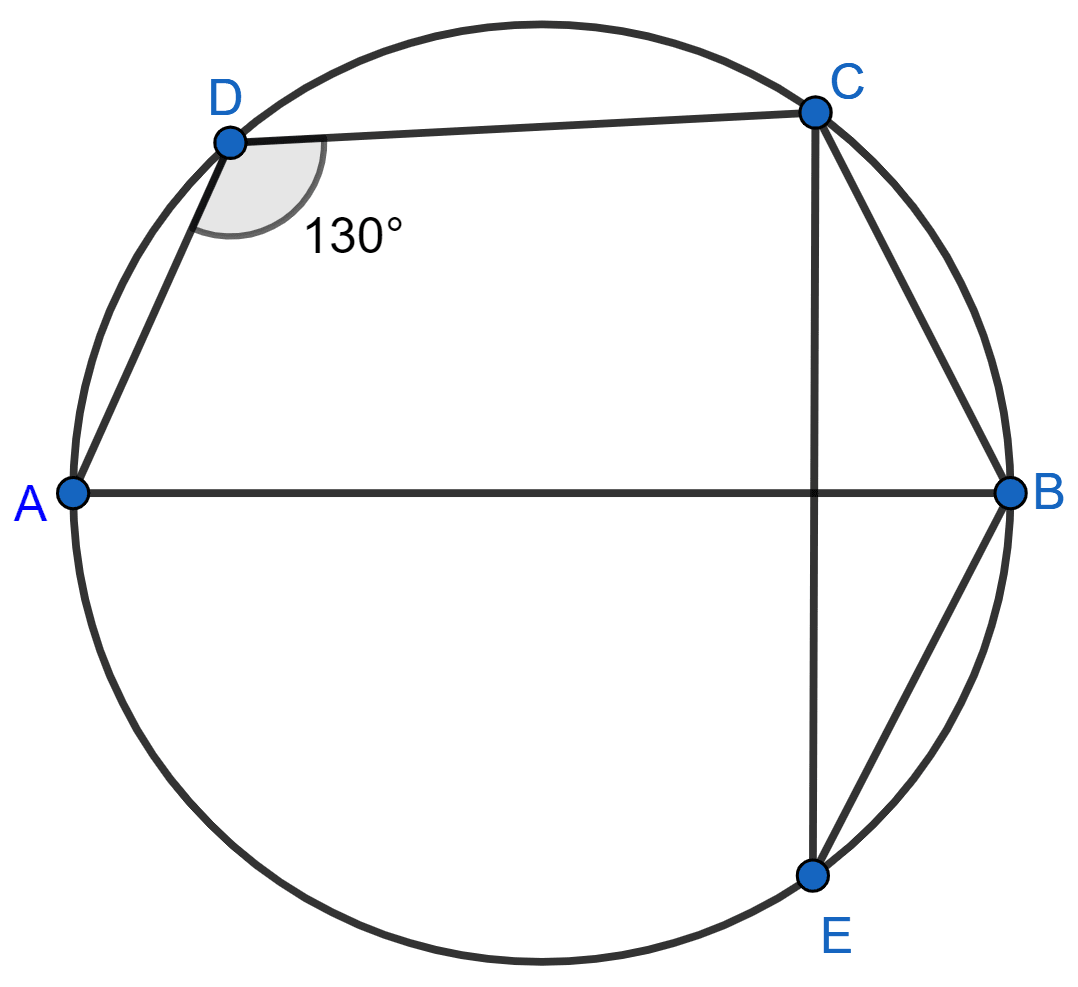
In the given figure, ∠ADC = 130° and BC = BE. Find ∠CBE if AB ⊥ CE.
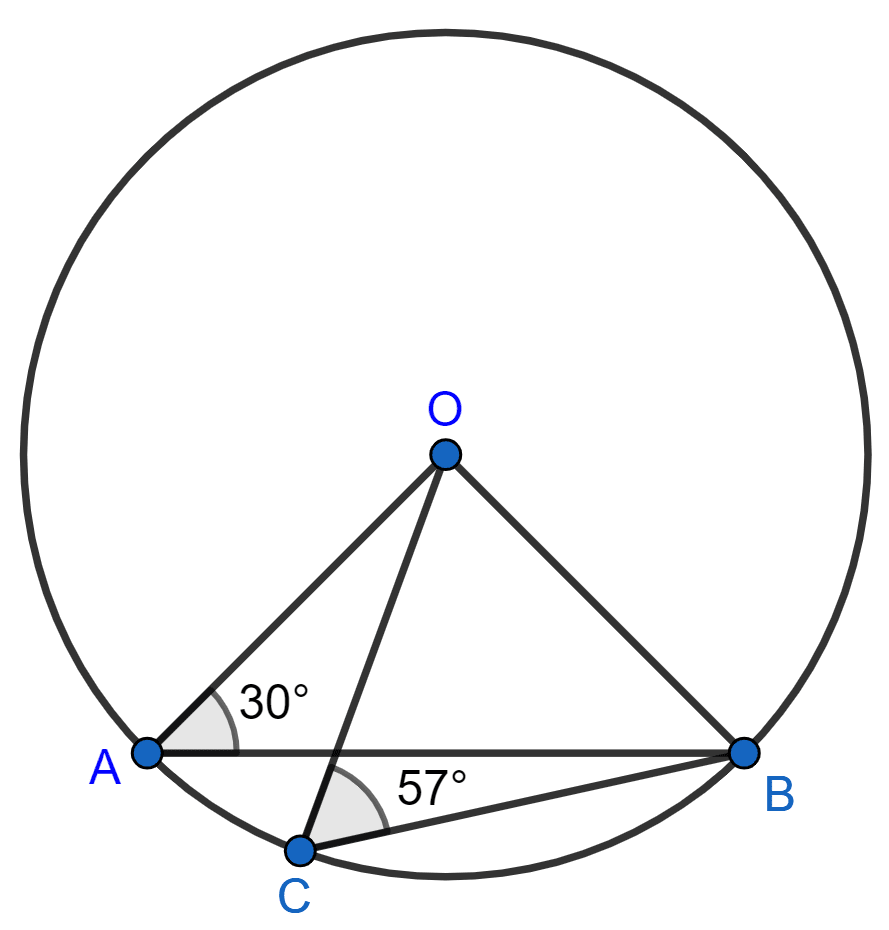
In the given figure, ∠OAB = 30° and ∠OCB = 57°, find ∠BOC and ∠AOC.
In the given figure, AB and XY are diameters of a circle with center O. If ∠APX = 30°, find :
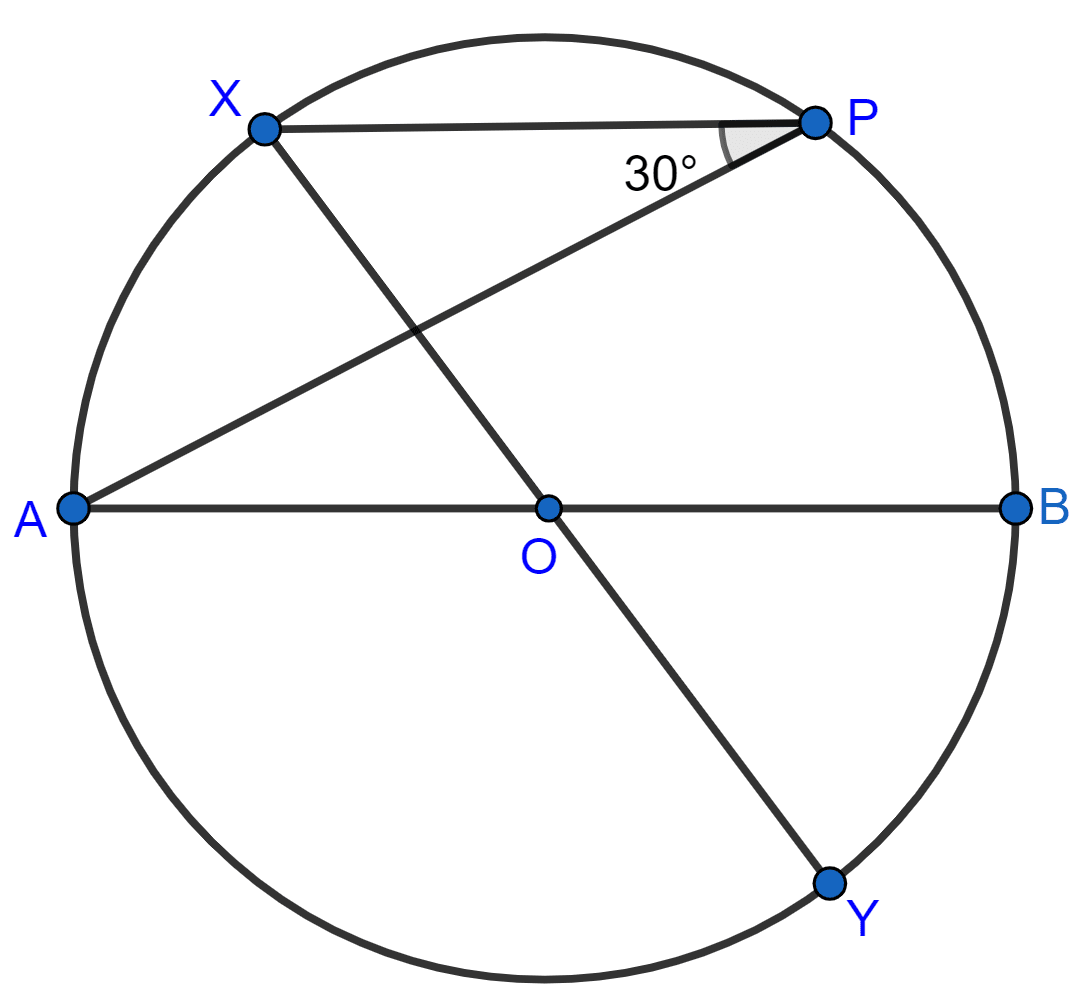
(i) ∠AOX
(ii) ∠APY
(iii) ∠BPY
(iv) ∠OAX
In the adjoining figure; AB = AD, BD = CD and ∠DBC = 2∠ABD. Prove that : ABCD is a cyclic quadrilateral.
