Mathematics
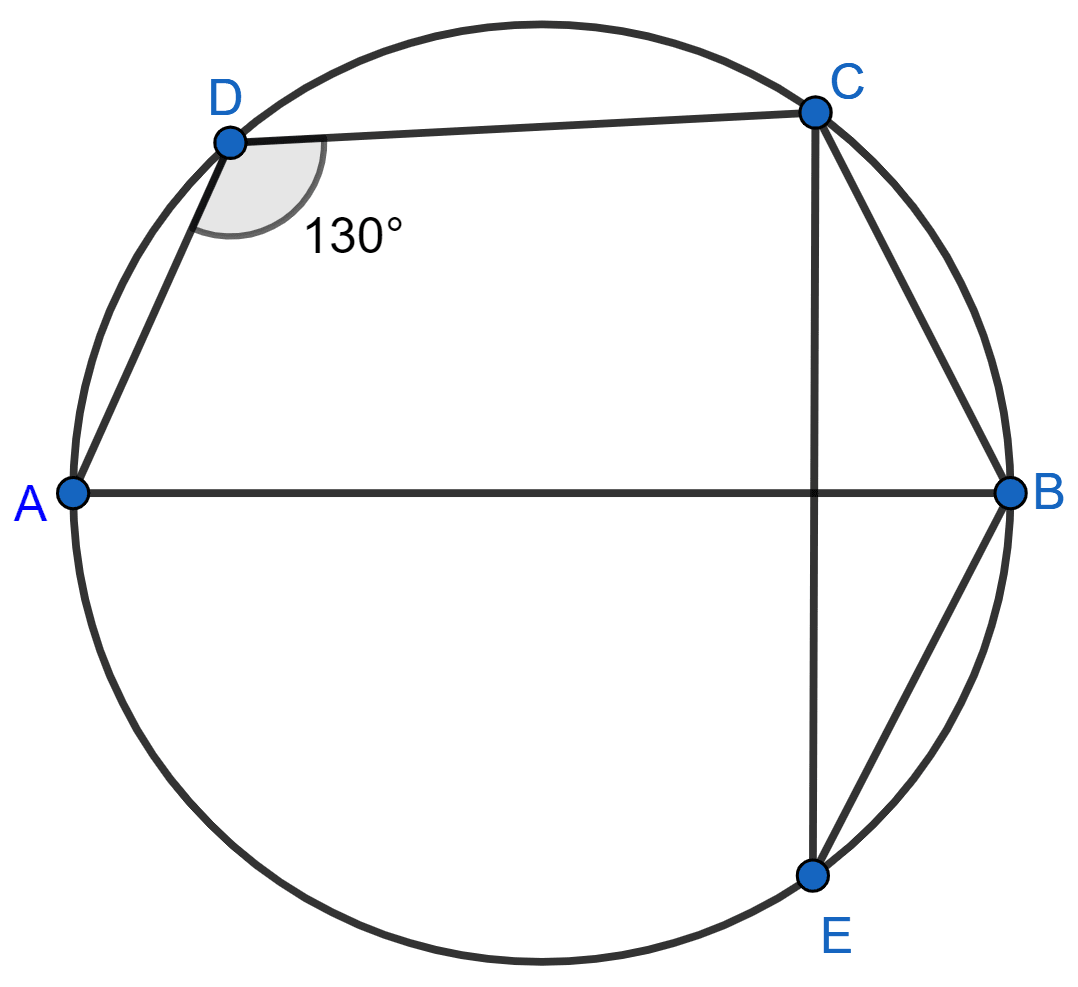
In the given figure, ∠ADC = 130° and BC = BE. Find ∠CBE if AB ⊥ CE.
Circles
7 Likes
Answer
Since, ABCD is a cyclic quadrilateral and sum of opposite angles in a cyclic quadrilateral = 180°.
∴ ∠ADC + ∠ABC = 180°
⇒ 130° + ∠ABC = 180°
⇒ ∠ABC = 50°.
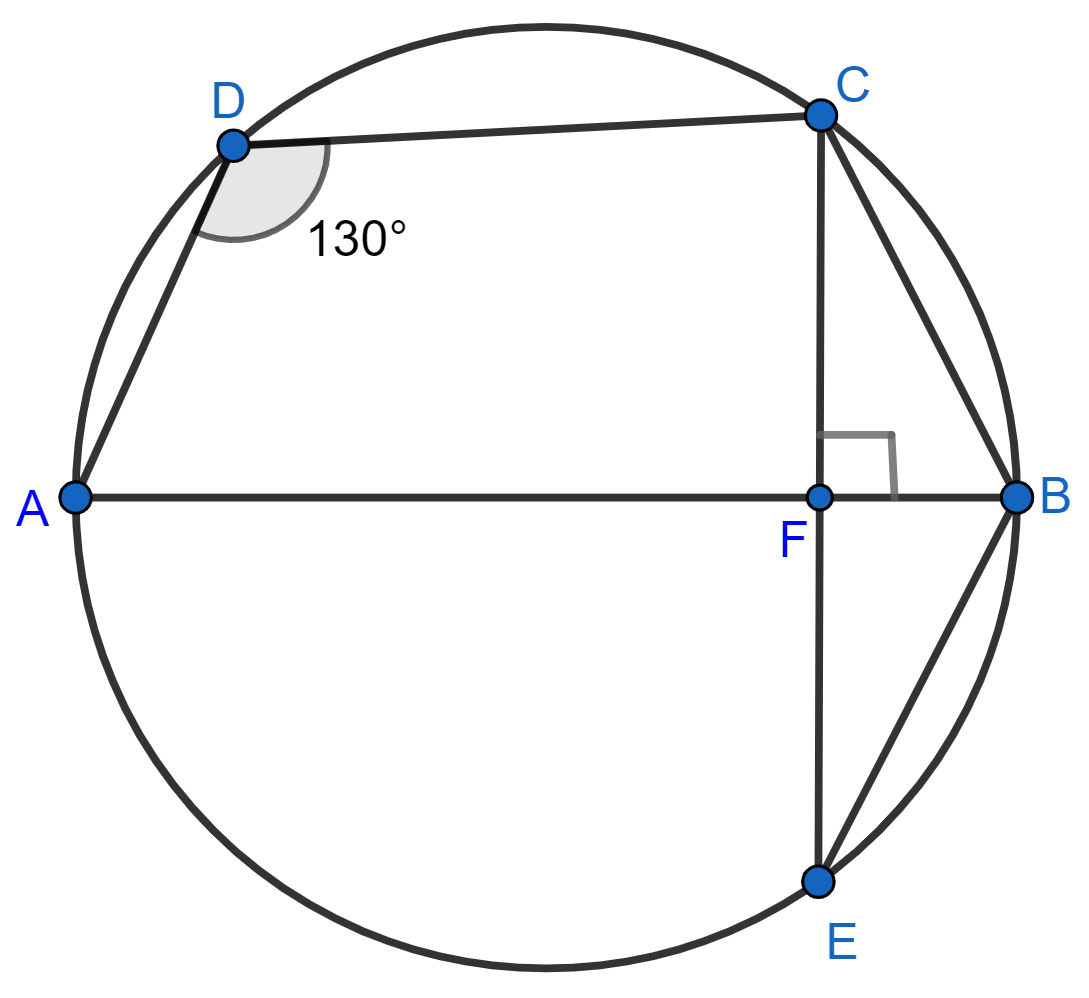
From figure,
⇒ ∠FBC = ∠ABC = 50°.
In △FBC,
By angle sum property of triangle,
⇒ ∠FBC + ∠BCF + ∠CFB = 180°
⇒ 50° + ∠BCF + 90° = 180°
⇒ ∠BCF = 180° - 90° - 50° = 40°.
Given,
BC = BE
In △BCE,
⇒ ∠BEC = ∠BCE = 40°. (As angles opposite to equal sides are equal)
In △FBE,
By angle sum property of triangle,
⇒ ∠BEF + ∠FBE + ∠EFB = 180°
⇒ 40° + ∠FBE + 90° = 180°
⇒ ∠FBE = 180° - 90° - 40° = 50°.
From figure,
∠CBE = ∠FBC + ∠FBE = 50° + 50° = 100°.
Hence, ∠CBE = 100°.
Answered By
4 Likes
Related Questions
Use graph paper for this question. Take 2 cm = 1 unit on both axes.
(i) Plot the points A(1, 1), B(5, 3) and C(2, 7).
(ii) Construct the locus of points equidistant from A and B.
(iii) Construct the locus of points equidistant from AB and AC.
(iv) Locate the point P such that PA = PB and P is equidistant from AB and AC.
(v) Measure and record the length PA in cm.
The speed of sound is 332 meters per second. A gun is fired. Describe the locus of all the people on the earth's surface, who hear the sound exactly one second later.
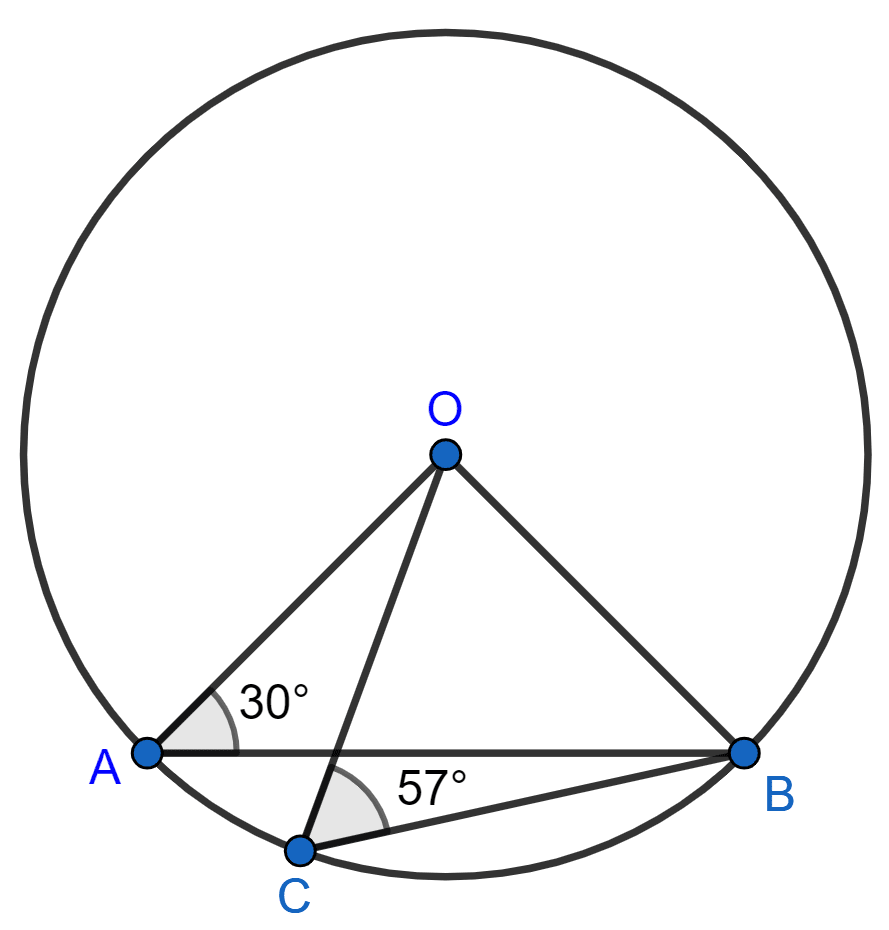
In the given figure, ∠OAB = 30° and ∠OCB = 57°, find ∠BOC and ∠AOC.
In the given figure, O is the center of the circle. If chord AB = chord AC, OP ⊥ AB and OQ ⊥ AC; show that : PB = QC.