Mathematics
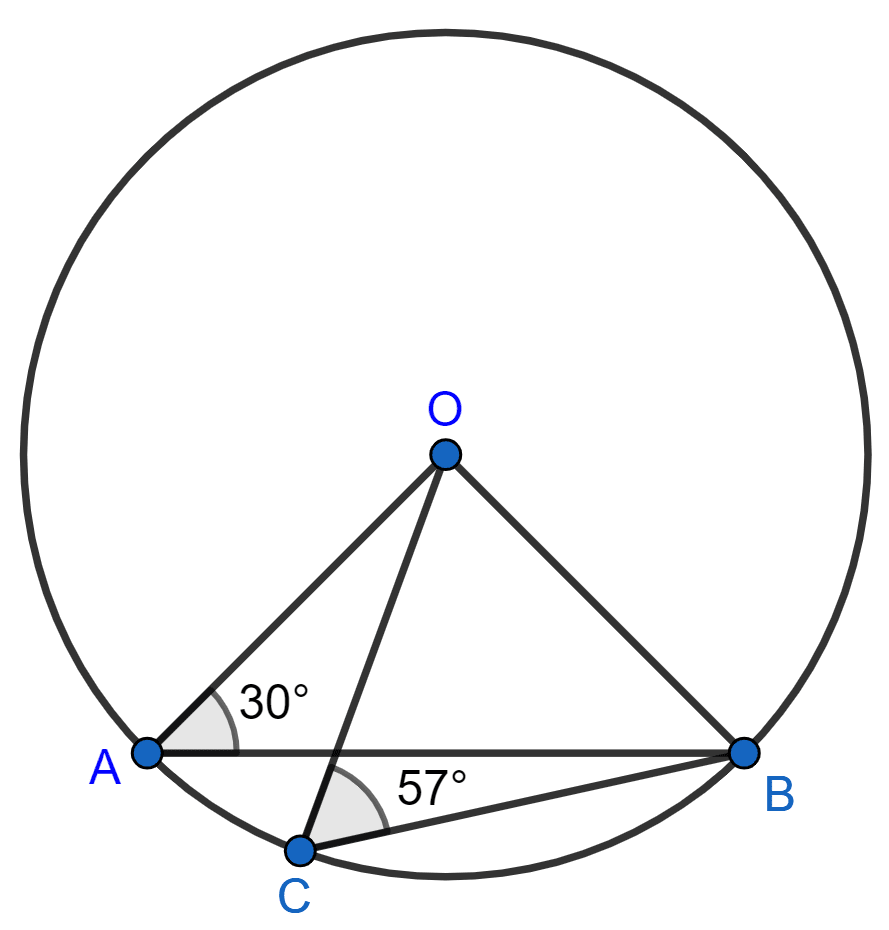
In the given figure, ∠OAB = 30° and ∠OCB = 57°, find ∠BOC and ∠AOC.
Circles
10 Likes
Answer
In △AOB,
⇒ OA = OB [Radius of same circle]
⇒ ∠OBA = ∠BAO = 30° [Angles opposite to equal sides are equal]
Also,
⇒ ∠OBA + ∠BAO + ∠AOB = 180° [By angles sum property of triangle]
⇒ 30° + 30° + ∠AOB = 180°
⇒ ∠AOB = 180° - 60° = 120°
In △OCB,
OC = OB [Radius of same circle]
⇒ ∠OBC = ∠OCB = 57° [Angles opposite to equal sides are equal]
Also,
⇒ ∠OCB + ∠OBC + ∠BOC = 180° [By angles sum property of triangle]
⇒ 57° + 57° + ∠BOC = 180°
⇒ ∠BOC = 180° - 114° = 66°
From figure,
⇒ ∠AOB = ∠AOC + ∠BOC
⇒ 120° = ∠AOC + 66°
⇒ ∠AOC = 120° - 66° = 54°.
Hence, ∠AOC = 54° and ∠BOC = 66°.
Answered By
7 Likes
Related Questions
The speed of sound is 332 meters per second. A gun is fired. Describe the locus of all the people on the earth's surface, who hear the sound exactly one second later.
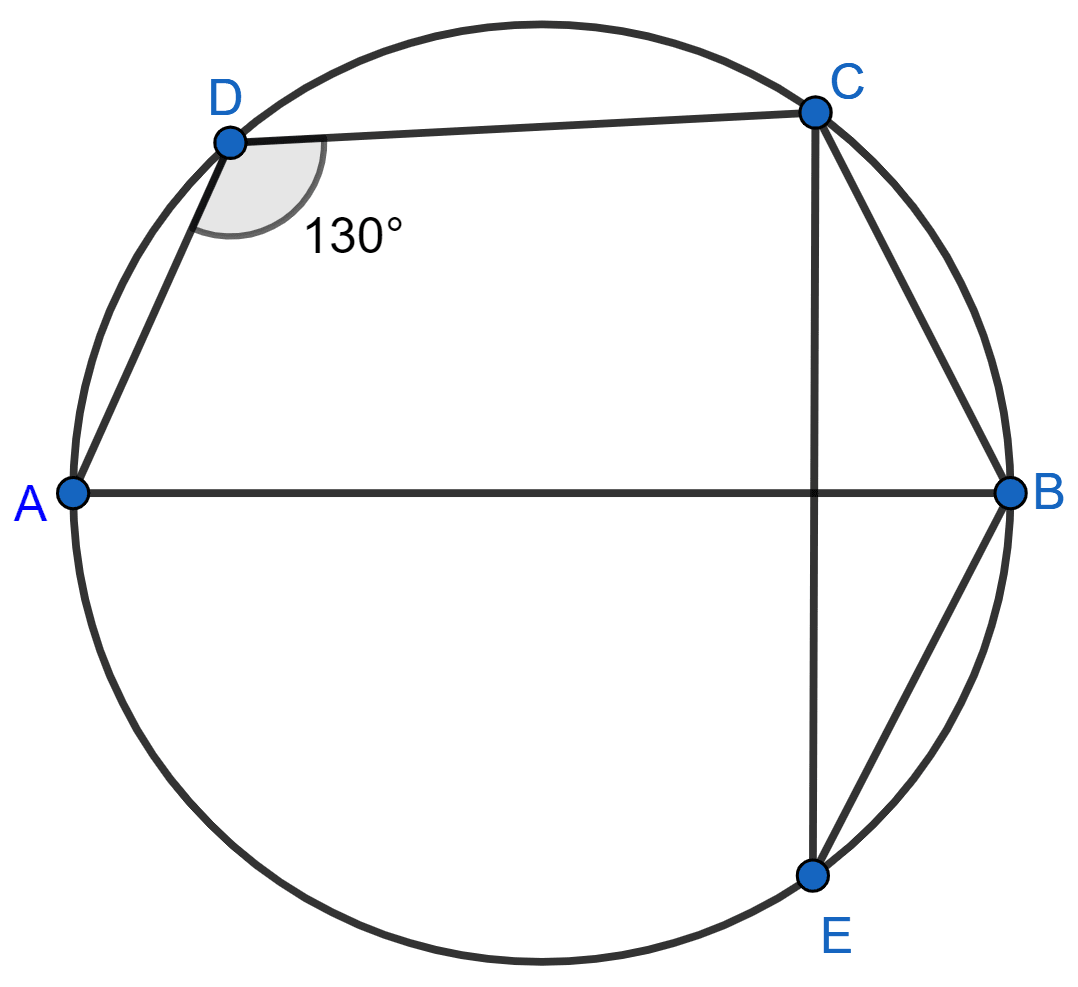
In the given figure, ∠ADC = 130° and BC = BE. Find ∠CBE if AB ⊥ CE.
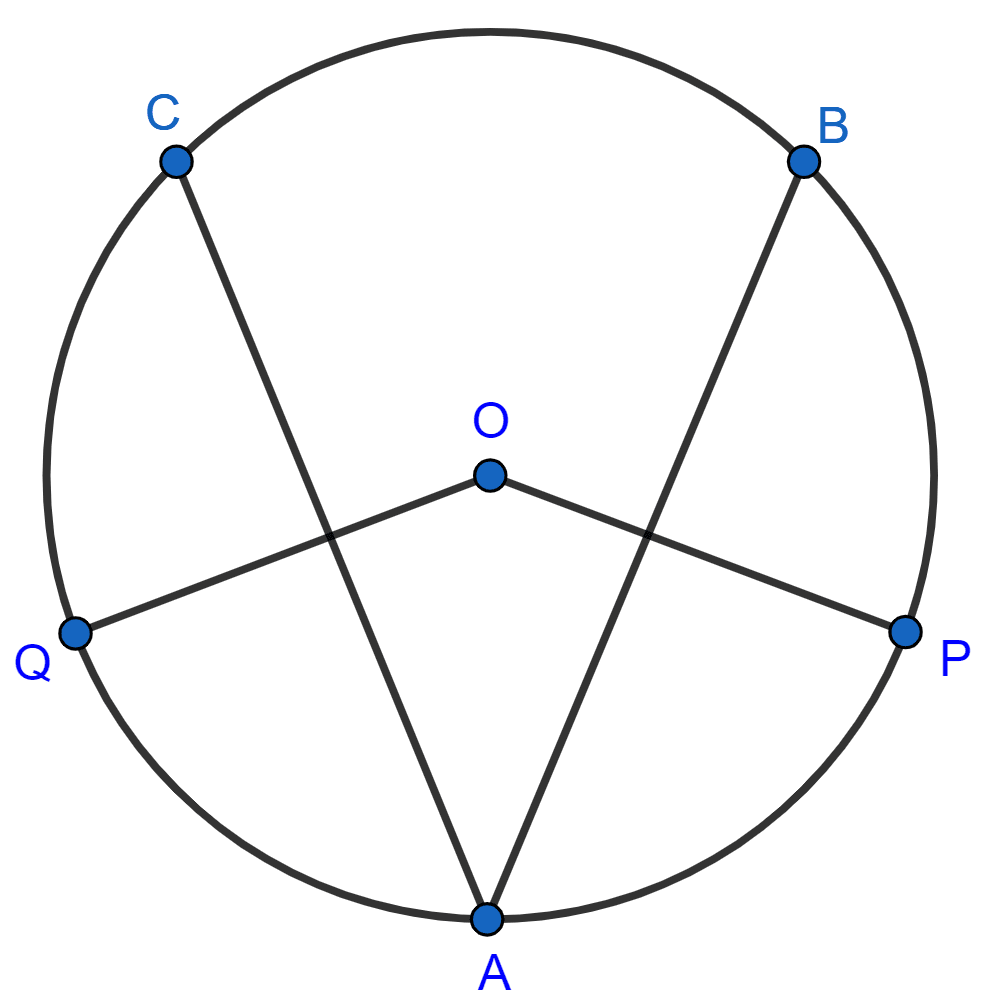
In the given figure, O is the center of the circle. If chord AB = chord AC, OP ⊥ AB and OQ ⊥ AC; show that : PB = QC.
In the given figure, AB and XY are diameters of a circle with center O. If ∠APX = 30°, find :
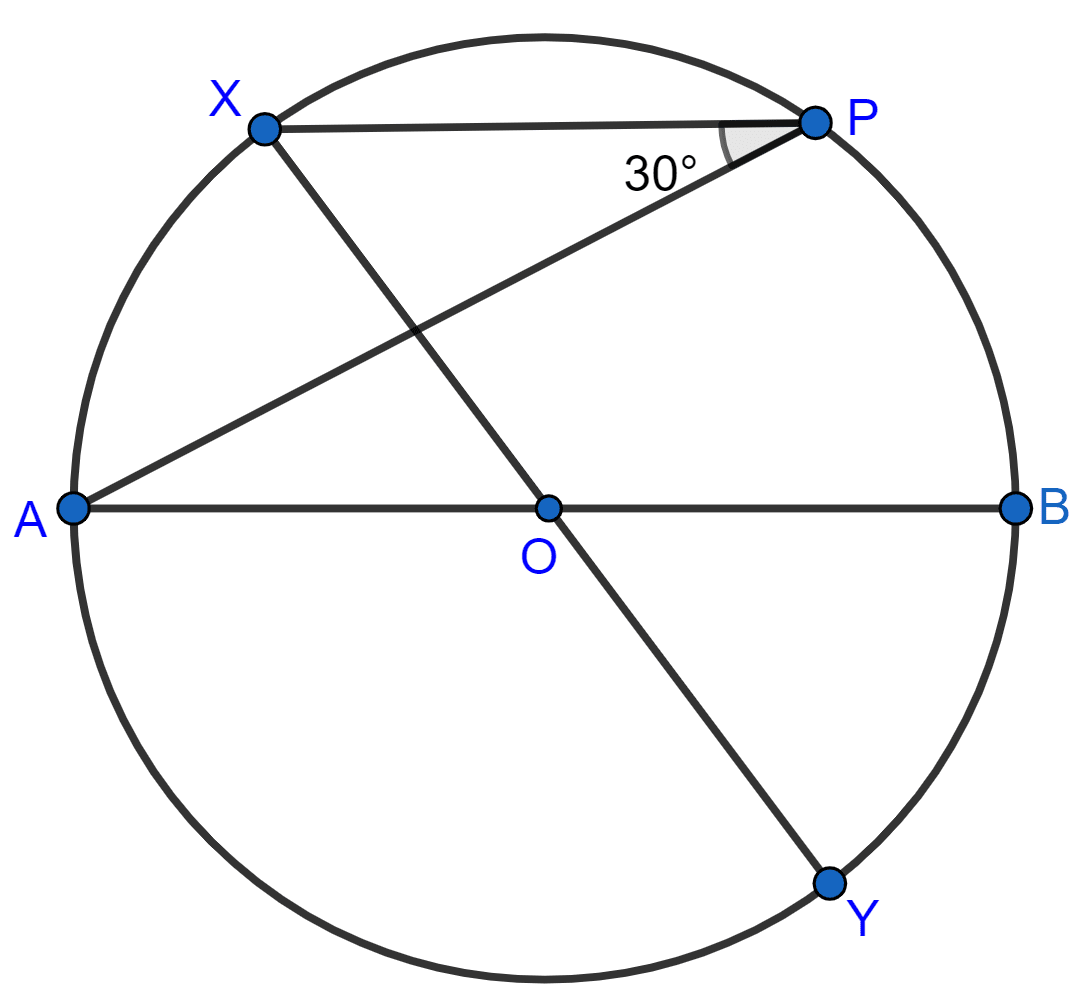
(i) ∠AOX
(ii) ∠APY
(iii) ∠BPY
(iv) ∠OAX