Mathematics
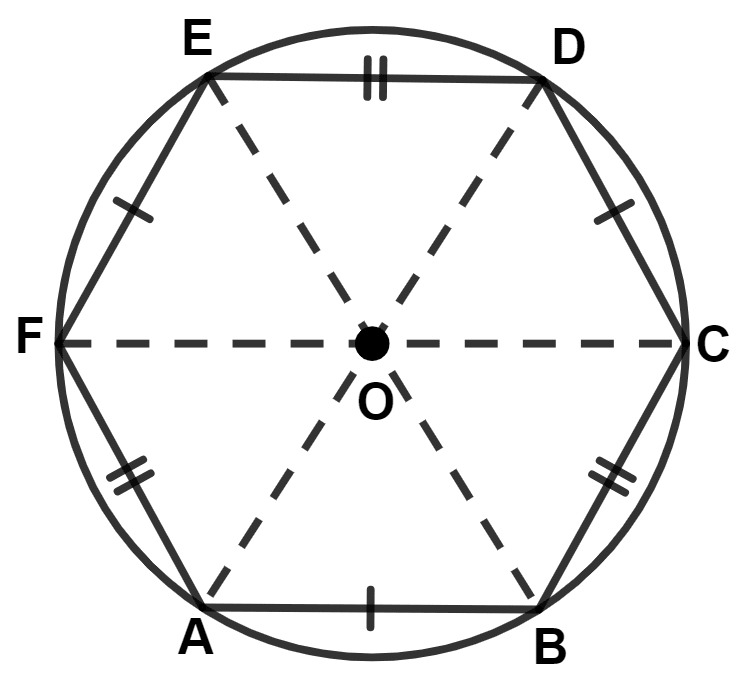
In the given figure, O is the center of the circle, chords AB, CD and EF are equal whereas chords BC, DE and FA are separately equal. The angle AOC is equal to :
80°
100°
90°
120°
Circles
8 Likes
Answer
Given,
Chords AB, CD and EF are equal.
∴ ∠AOB = ∠COD = ∠EOF = x (let)
Chords BC, DE and FA are equal.
∴ ∠BOC = ∠DOE = ∠AOF = y (let)
From figure,
⇒ ∠AOB + ∠COD + ∠EOF + ∠BOC + ∠DOE + ∠AOF = 360°
⇒ x + x + x + y + y + y = 360°
⇒ 3x + 3y = 360°
⇒ 3(x + y) = 360°
⇒ x + y =
⇒ x + y = 120°
From figure,
∠AOC = ∠AOB + ∠BOC = x + y = 120°.
Hence, Option 4 is the correct option.
Answered By
6 Likes
Related Questions
In the given figure, O is the center of the circle, AB is side of a regular pentagon, then angle ACB is equal to :
36°
72°
50°
40°

In a cyclic-trapezium, the non-parallel sides are equal and the diagonals are also equal. Prove it.
In the given figure, O is the center of a circle. AB is the side of a square and BC is side of a regular hexagon. Also arc AD = arc CD. Angle DOC is equal to :
150°
105°
130°
210°
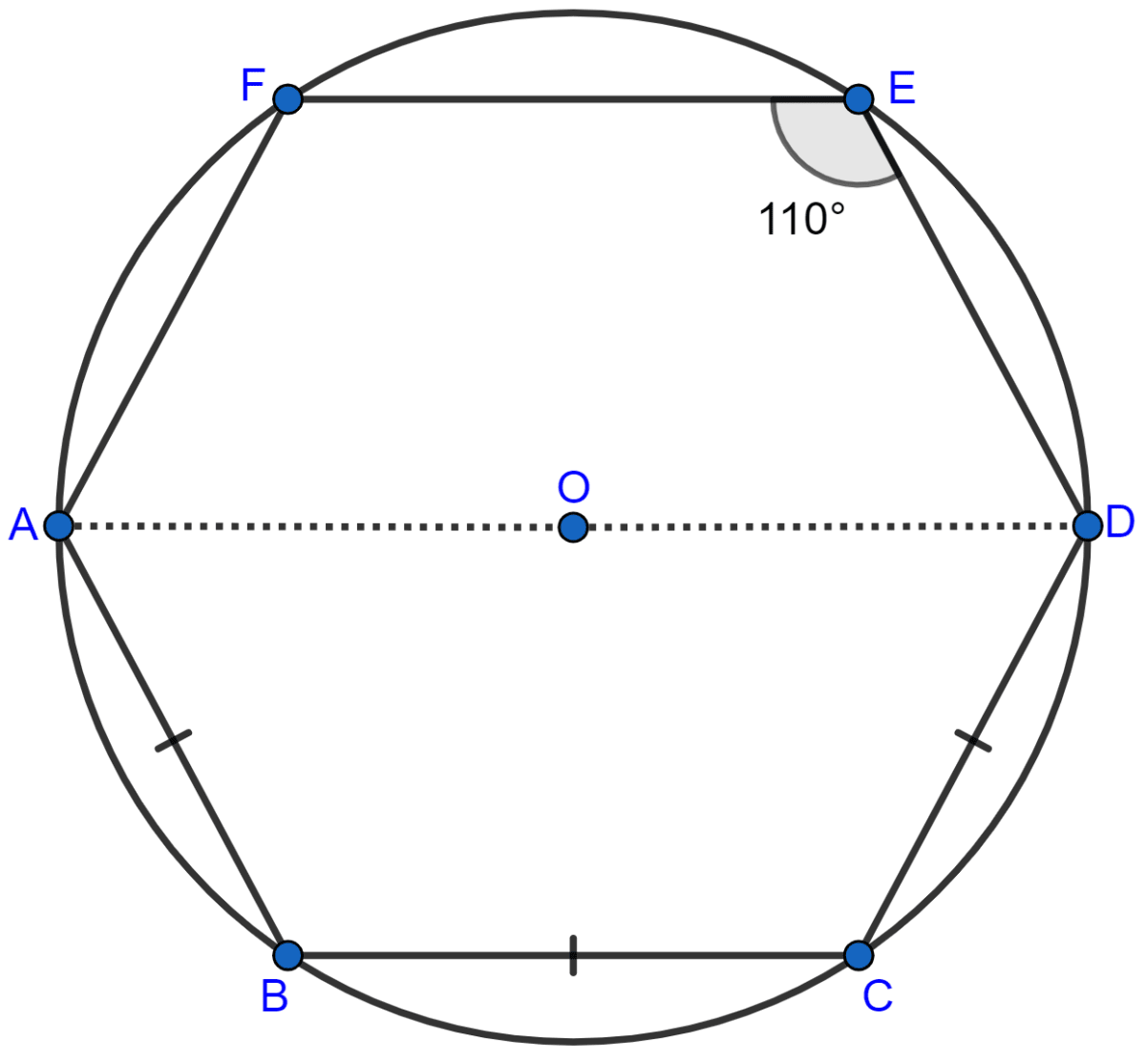
In the following figure, AD is the diameter of the circle with centre O. Chords AB, BC and CD are equal. If ∠DEF = 110°, calculate :
(i) ∠AEF, (ii) ∠FAB.