Mathematics
In the given figure, O is center of the circle and angle OBA = 50°. The angle P is :
50°
80°
40°
60°

Circles
11 Likes
Answer
From figure,
In △ OAB,
OA = OB (Radius of common circle)
We know that,
Angles opposite to equal sides of a triangle are equal.
∴ ∠A = ∠B = 50°
By angle sum property of triangle,
⇒ ∠A + ∠B + ∠O = 180°
⇒ 50° + 50° + ∠O = 180°
⇒ ∠O + 100° = 180°
⇒ ∠O = 180° - 100° = 80°.
We know that,
The angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.
⇒ ∠O = 2∠P
⇒ ∠P = = 40°.
Hence, Option 3 is the correct option.
Answered By
9 Likes
Related Questions
In the given figure, O is center of the circle and ∠B = 55°. The angle A is equal to :
55°
35°
45°
50°

In the given figure, chord AB = chord PB and angle C = 50°. The angle PAB is equal to :
65°
50°
75°
60°

O' and O" are centers of two circles which intersect each other at points A and B. Then :
BC = BD
BC is larger than BD.
BC is smaller than BD.
C, B and D are collinear.

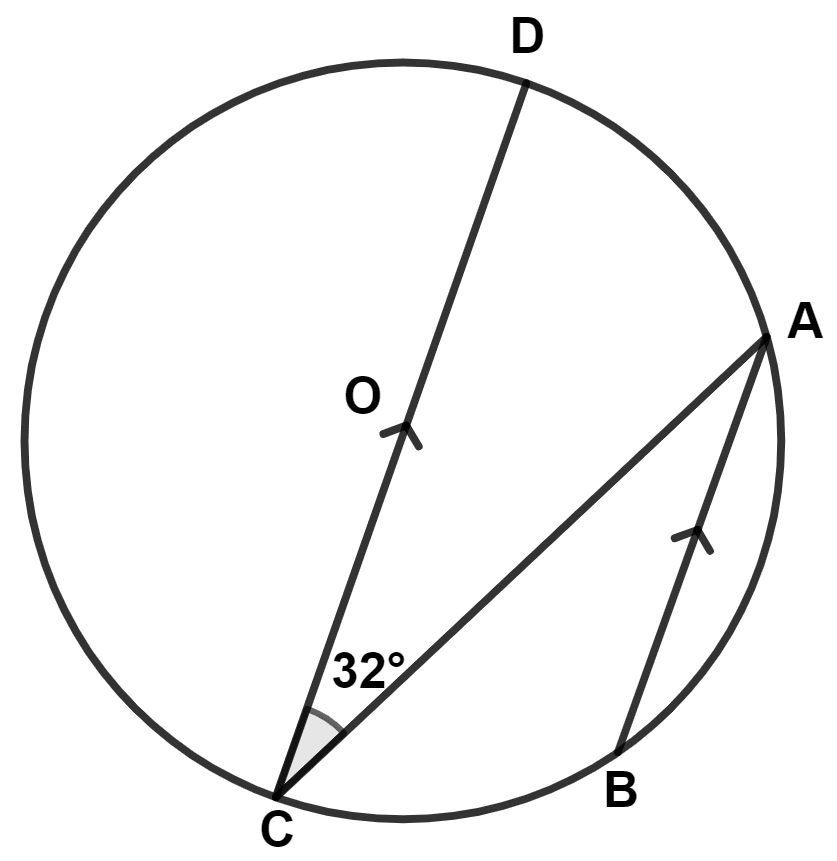
In the given figure, O is center of the circle, AB || DC and ∠ACD = 32°, ∠DAB is equal to :
122°
148°
90°
none of the above