Mathematics
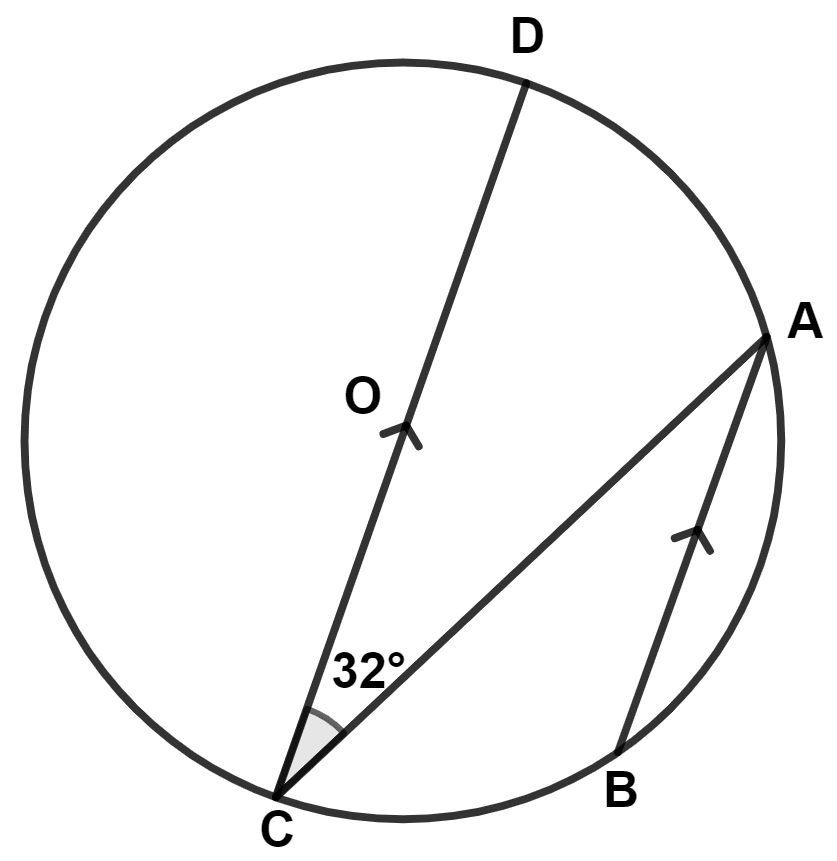
In the given figure, O is center of the circle, AB || DC and ∠ACD = 32°, ∠DAB is equal to :
122°
148°
90°
none of the above
Circles
14 Likes
Answer
Join DA.
From figure,
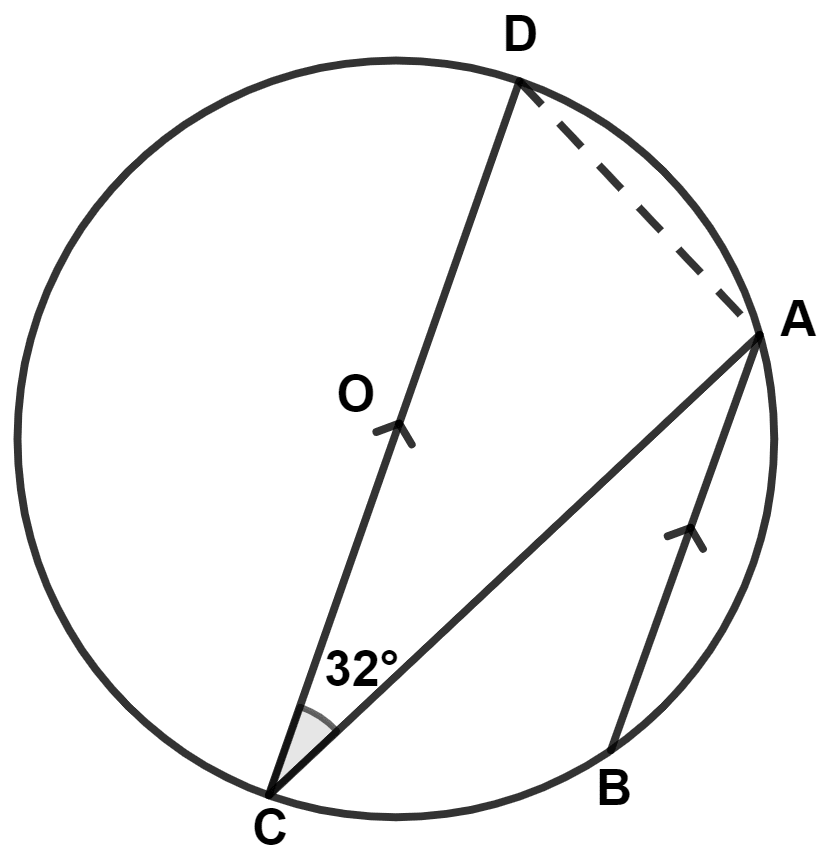
In △DAC,
∠DAC = 90° (Angle in semicircle is a right angle)
As, alternate angles are equal.
∴ ∠CAB = ∠ACD = 32°
From figure,
∠DAB = ∠DAC + ∠CAB = 90° + 32° = 122°.
Hence, Option 1 is the correct option.
Answered By
11 Likes
Related Questions
In the given figure, chord AB = chord PB and angle C = 50°. The angle PAB is equal to :
65°
50°
75°
60°

O' and O" are centers of two circles which intersect each other at points A and B. Then :
BC = BD
BC is larger than BD.
BC is smaller than BD.
C, B and D are collinear.

In the given figure, ∠BAD = 65°, ∠ABD = 70°, ∠BDC = 45°
(i) Prove that AC is a diameter of the circle.
(ii) Find ∠ACB

In the following figure, O is the center of the circle. Find the value of a.
