Mathematics
In the given figure, MN is the common chord of two intersecting circles and AB is their common tangent.
Prove that the line NM produced bisects AB at P.

Answer
We know that,
If a chord and a tangent intersect externally, then the product of the lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.
∴ AP2 = PM x PN ……….(1)
From P, PB is the tangent and PMN is the secant for second circle.
∴ PB2 = PM x PN ……… (2)
From (1) and (2), we have
⇒ AP2 = PB2
⇒ AP = PB
Hence, proved that P is the midpoint of AB.
Related Questions
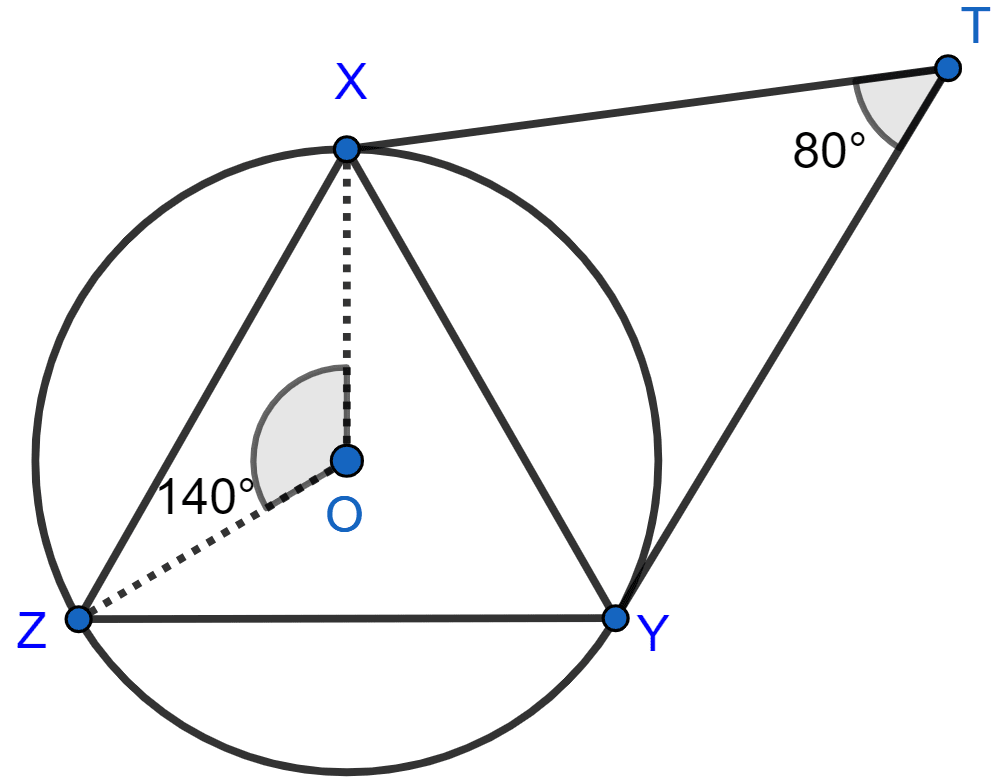
In the figure, given below, O is the center of the circumcircle of triangle XYZ. Tangents at X and Y intersect at point T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY.
In the given figure, AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find AE.

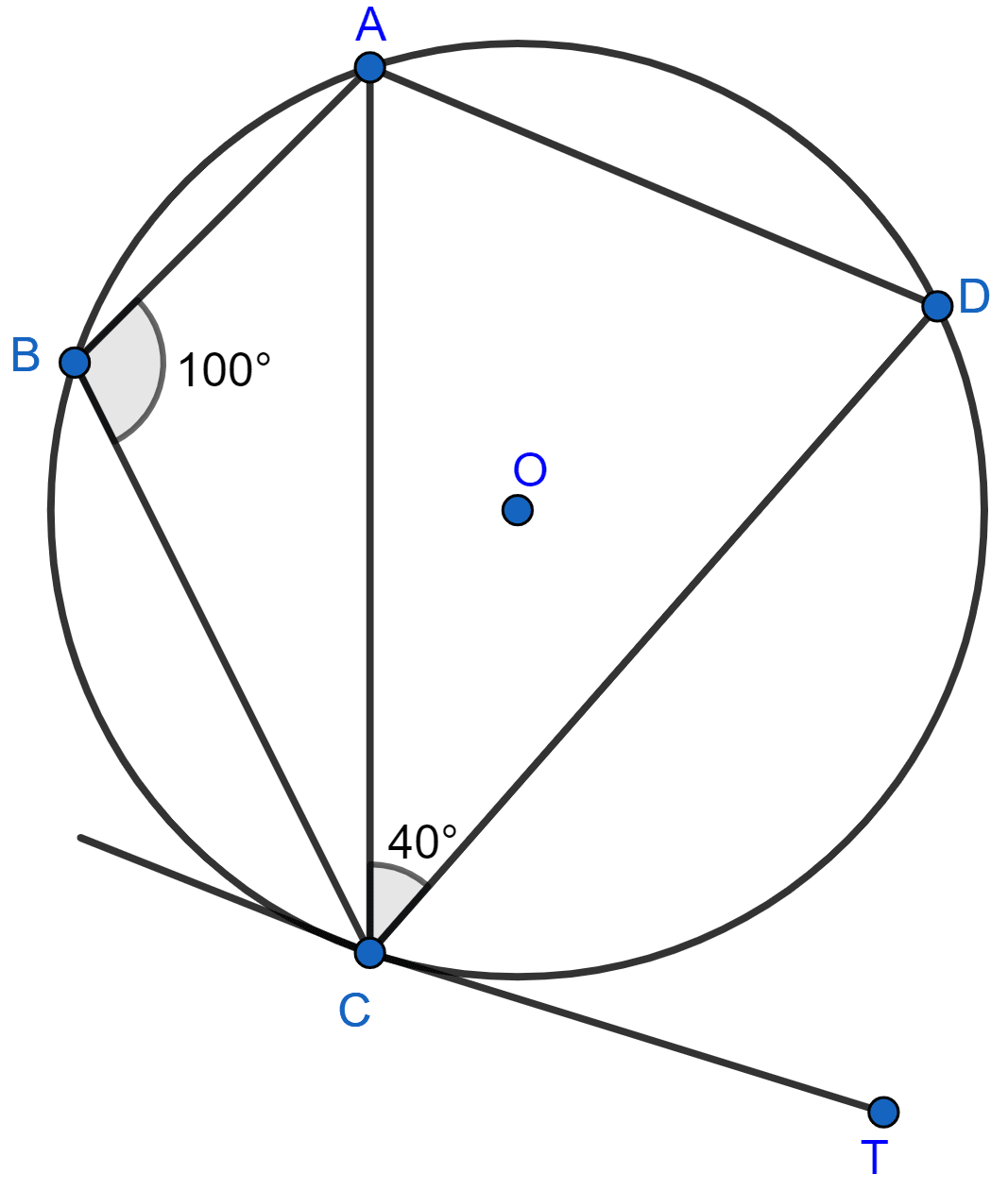
In the given circle with centre O, angle ABC = 100°, ∠ACD = 40° and CT is a tangent to the circle at C. Find ∠ADC and ∠DCT.
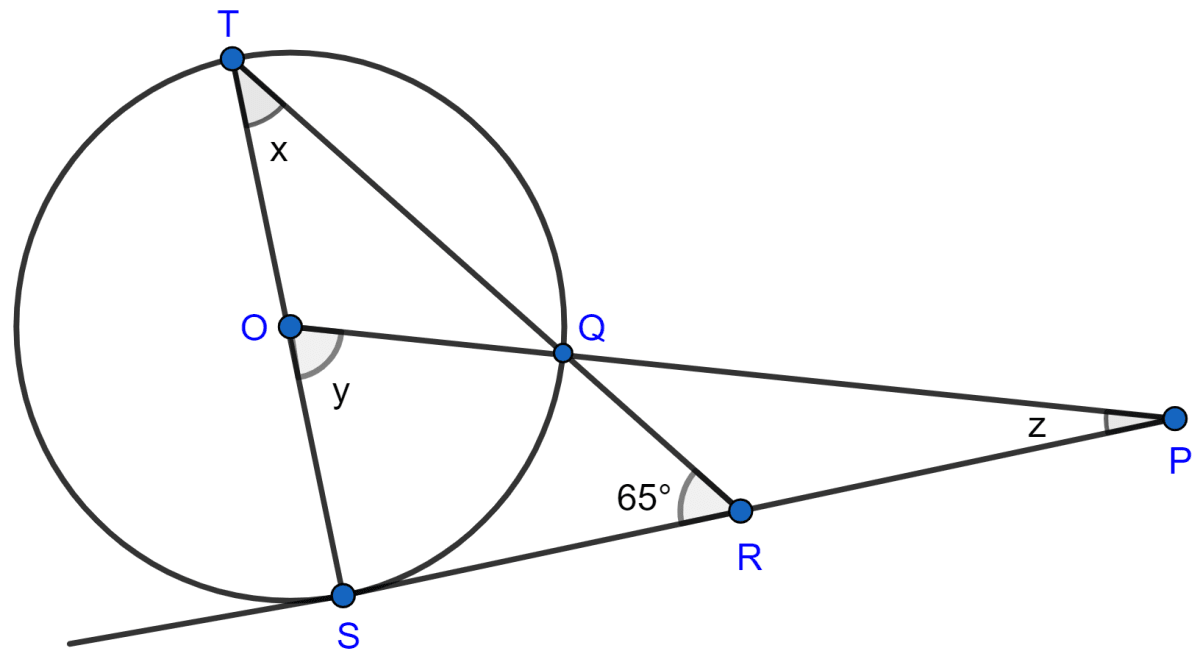
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the values of x, y and z.