Mathematics
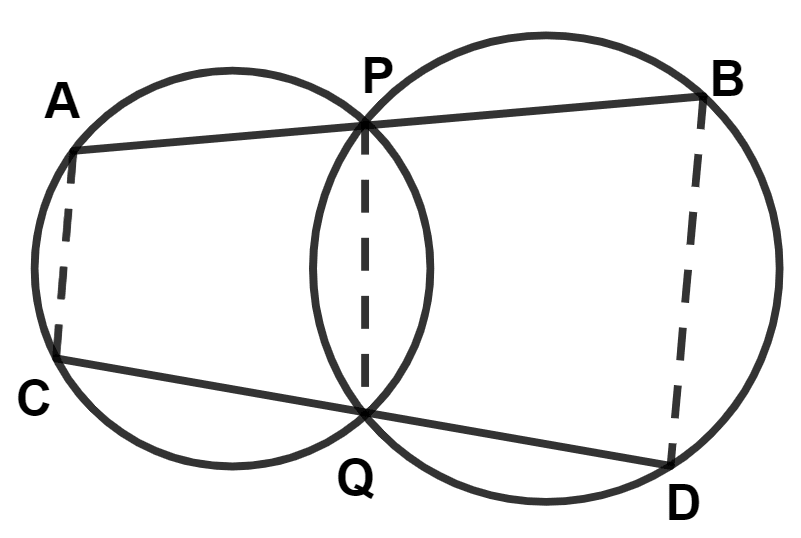
In the given figure APB and CQD are two straight lines, then :
AB || CD
AC || PQ
PQ || BD
AC || BD
Answer
Let ∠BPQ = x and ∠DQP = y
We know that,
The exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.
From figure,
In cyclic quadrilateral APQC,
∠A = ∠DQP = y and ∠C = ∠BPQ = x
From figure,
APB is a straight line.
∴ ∠APQ + ∠BPQ = 180°
⇒ ∠APQ + x = 180°
⇒ ∠APQ = 180° - x
CQD is a straight line.
∴ ∠CQP + ∠DQP = 180°
⇒ ∠CQP + y = 180°
⇒ ∠CQP = 180° - y
In cyclic quadrilateral PQDB,
∠B = ∠CQP = 180° - y and ∠D = ∠APQ = 180° - x
⇒ ∠A + ∠B = y + (180° - y) = 180°
⇒ ∠C + ∠D = x + (180° - x) = 180°
We know that,
Sum of adjacent angles in a trapezium is 180°.
∴ ABDC is a trapezium.
∴ AC || BD.
Hence, Option 4 is the correct option.
Related Questions
In the given figure, ABC is an equilateral triangle. Angle ADC is :
60°
100°
80°
120°

In the figure, given below, ∠ABC is equal to :
105°
75°
90°
45°

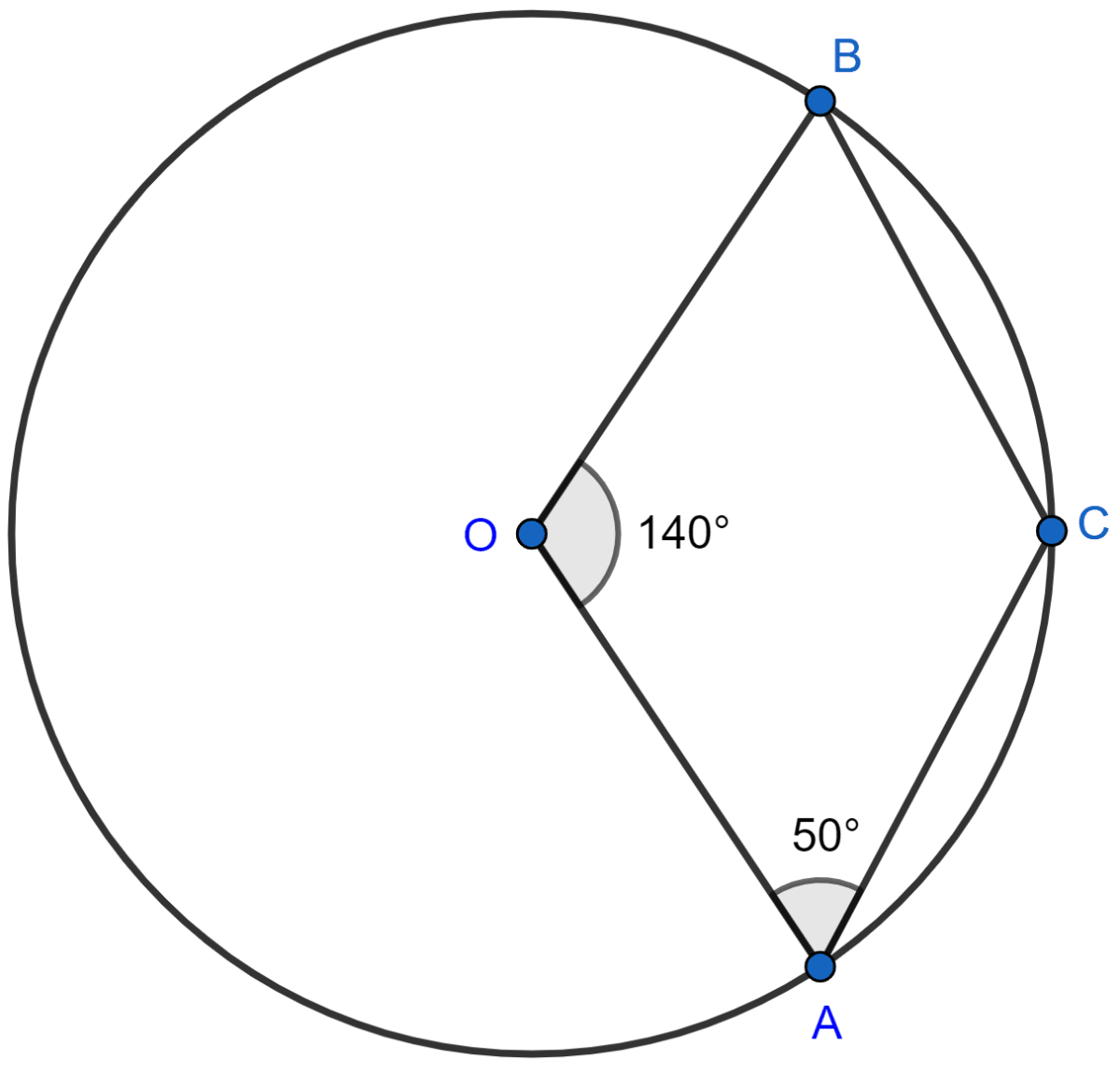
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find :
(i) ∠ACB,
(ii) ∠OBC,
(iii) ∠OAB,
(iv) ∠CBA.
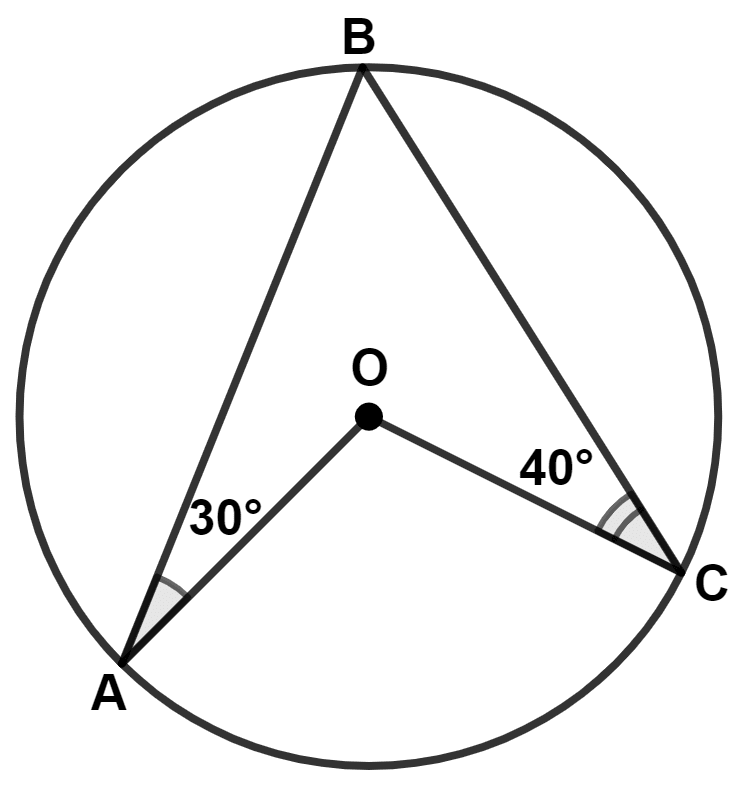
In the given figure, O is the center of the circle. ∠OAB and ∠OCB are 30° and 40° respectively. ∠AOC is equal to :
70°
80°
150°
140°