Mathematics
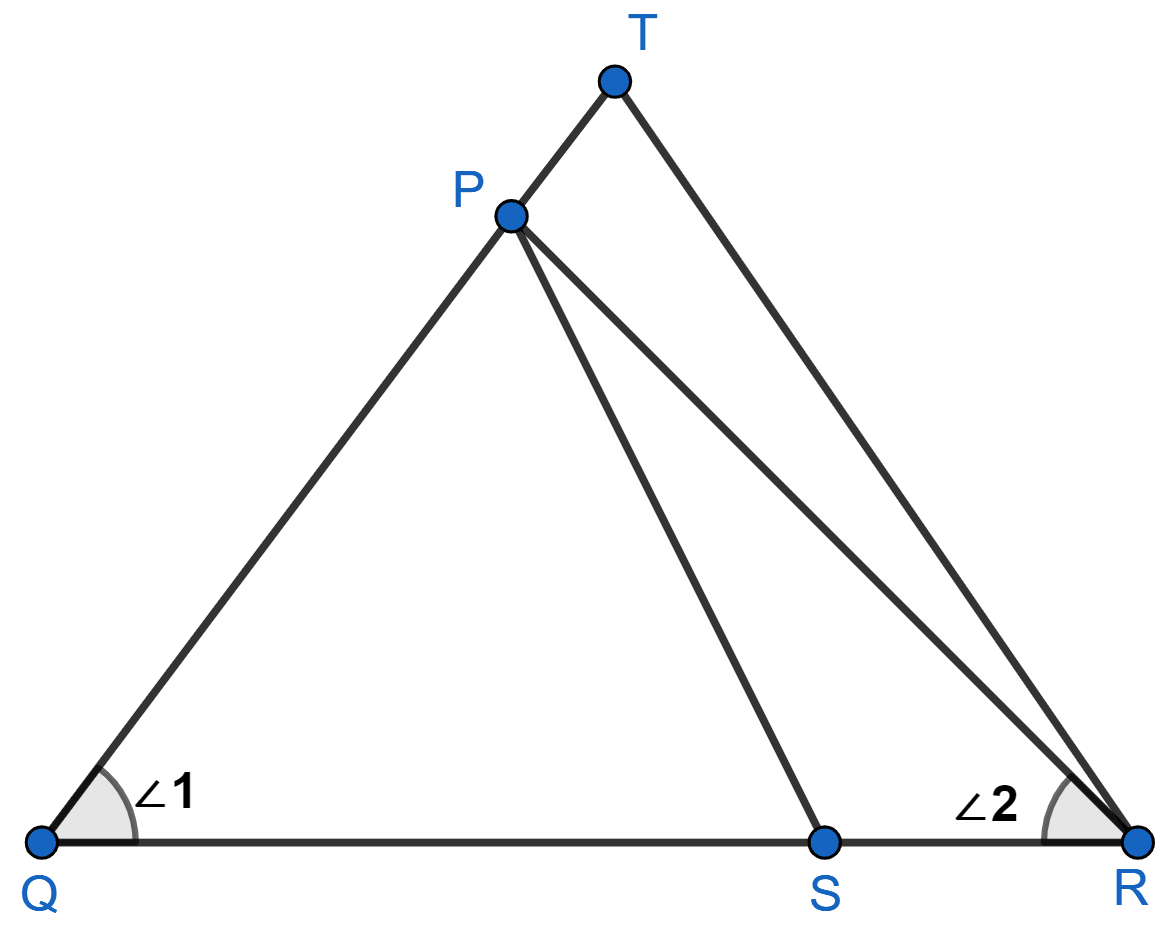
In the given figure, and ∠1 = ∠2. Show that △ PQS ~ △ TQR.
Triangles
Answer
In Δ PQR,
∠1 = ∠2 (Given)
⇒ PR = PQ (In a triangle sides opposite to equal angles are equal)
In Δ PQS and Δ TQR
⇒ ∠PQS = ∠TQR (Both = ∠1)
Given,
Since, PR = PQ.
∴ Δ PQS ~ Δ TQR (By SAS criterion)
Hence, proved that △ PQS ~ △ TQR.
Answered By
Related Questions
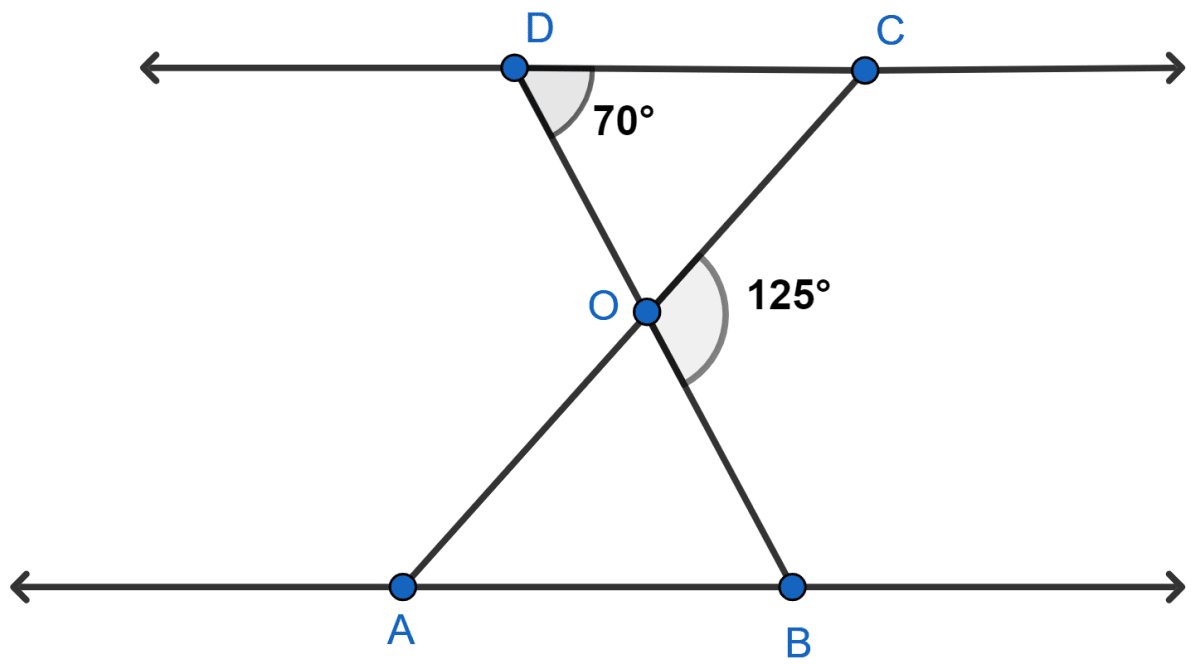
In given figure, △ ODC ~ △ OBA, ∠BOC = 125° and ∠CDO = 70°. Find ∠DOC, ∠DCO and ∠OAB.
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that .
S and T are points on sides PR and QR of △ PQR such that ∠P = ∠RTS. Show that △ RPQ ~ △ RTS.
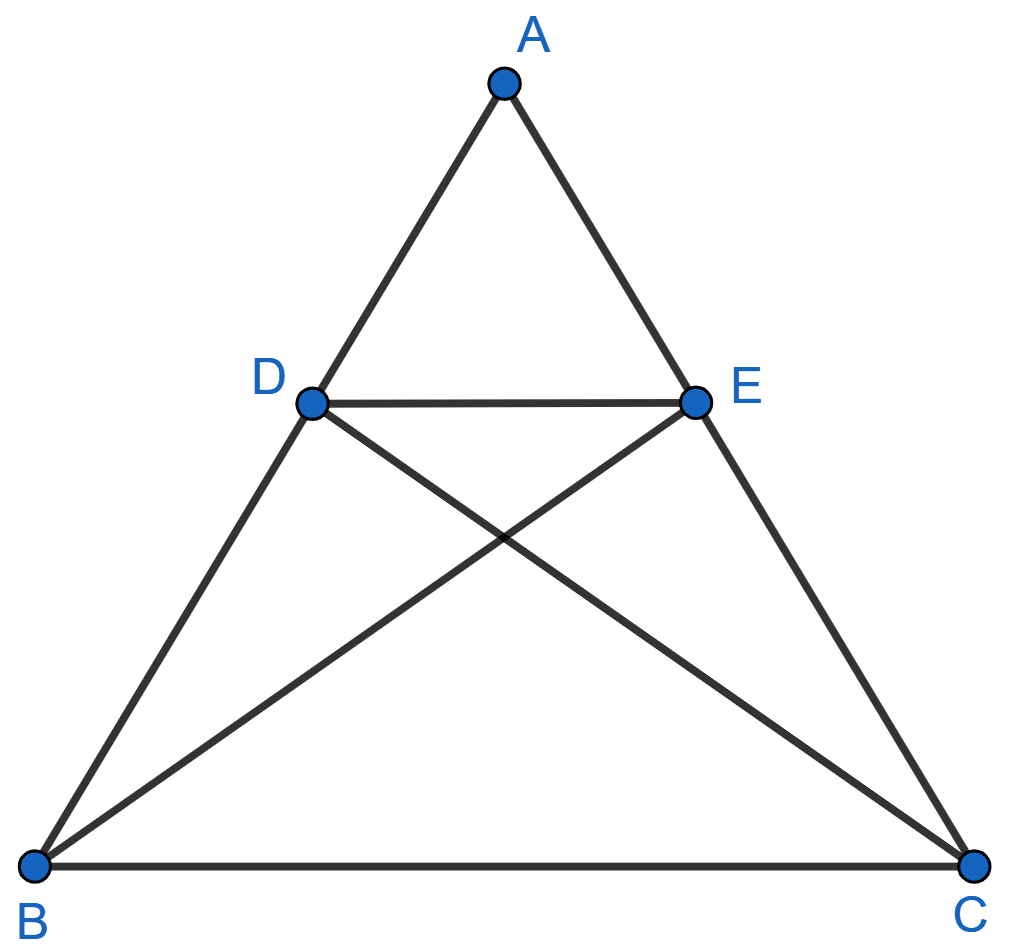
In given figure, if △ ABE ≅ Δ ACD, show that
△ ADE ∼ Δ ABC.