Mathematics
In the given figure, ABC is a triangle. DE is parallel to BC and AD/DB = 3/2. (i) Determine the ratios AD/AB and DE/BC. (ii) Prove that △DEF is similar to △CBF. Hence, find EF/FB. (iii) What is the ratio of the areas of △DEF and △BFC?
Related Questions
In the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2. DP produced meets AB produced at Q. Given the area of triangle CPQ = 20 cm2.
Calculate :
(i) area of triangle CDP,
(ii) area of parallelogram ABCD.

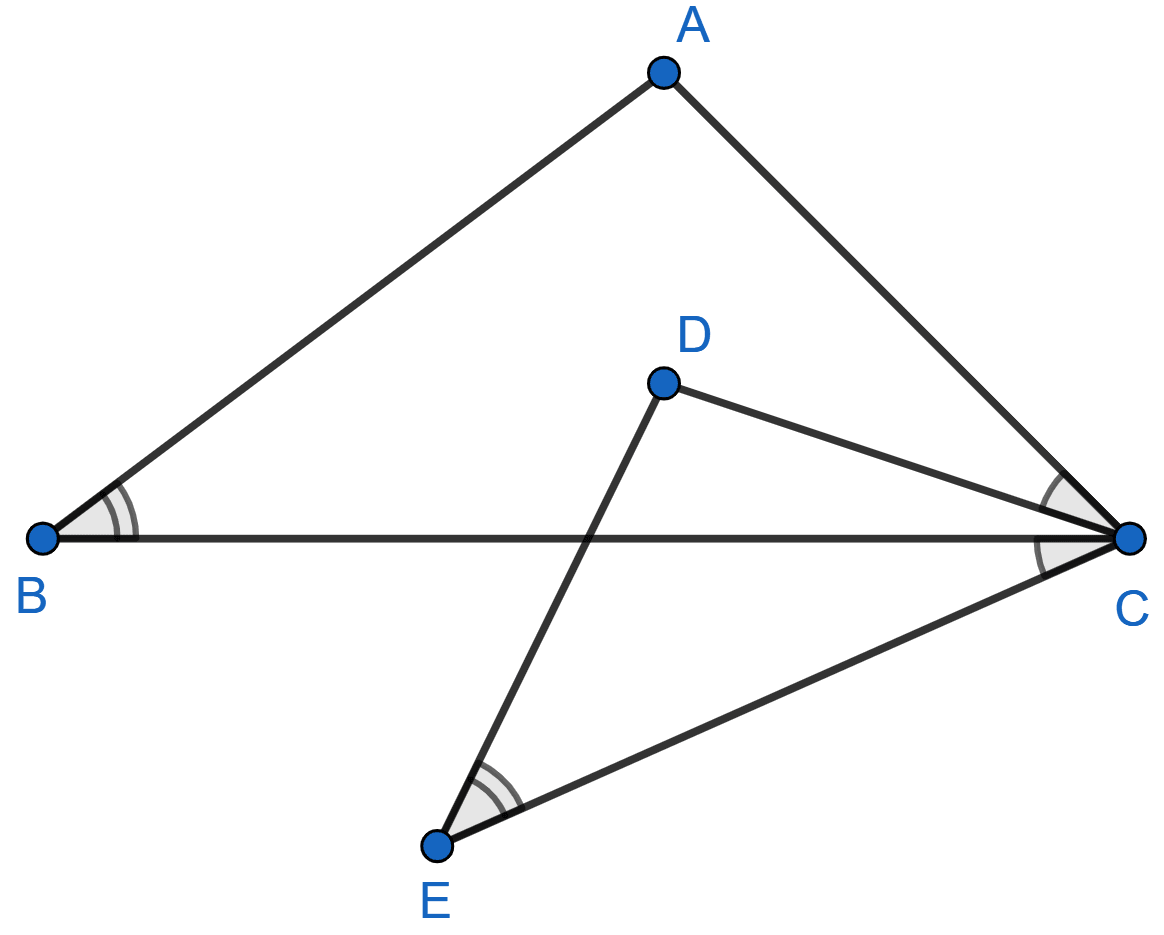
In the given figure,
∠B = ∠E, ∠ACD = ∠BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the △ABC and △DEC.
In the given figure, BC is parallel to DE. Area of triangle ABC = 25 cm2, Area of trapezium BCED = 24 cm2 and DE = 14 cm. Calculate the length of BC.
Also, find the area of triangle BCD.
