Mathematics
In the given figure, AB is the diameter of a circle with center O. If chord AC = chord AD, prove that :
(i) arc BC = arc DB
(ii) AB is the bisector of ∠CAD.
Further, if the length of arc AC is twice the length of arc BC, find :
(a) ∠BAC
(b) ∠ABC

Circles
Answer
Join BC and BD.

In △ABC and △ABD,
⇒ AC = AD [Given]
⇒ AB = AB [Common]
⇒ ∠ACB = ∠ADB [Both = 90°, Angle in semi-circle is a right angle.]
∴ △ ABC ≅ △ ABD [By RHS axiom of congruency]
(i) Since,
△ABC ≅ △ABD
∴ BC = BD [By C.P.C.T.]
∴ Arc BC = Arc BD [Equal chords have equal arcs].
Hence, proved that arc BC = arc BD.
(ii) Since,
△ABC ≅ △ABD
∴ ∠BAC = ∠BAD [By C.P.C.T.]
∴ AB is the bisector of ∠CAD.
Hence, proved that AB is the bisector of ∠CAD.
(a) Given,
arc AC = 2 arc BC
∴ ∠ABC = 2∠BAC
But,
⇒ ∠ABC + ∠BAC = 90° [ΔABC is right angled at C]
⇒ 2∠BAC + ∠BAC = 90°
⇒ 3∠BAC = 90°
⇒ ∠BAC = = 30°.
Hence, ∠BAC = 30°.
(b) ∠ABC = 2∠BAC = 2 x 30° = 60°.
Hence, ∠ABC = 60°.
Answered By
Related Questions
In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC. If the bisector of angle A meets BC at point E and the given circle at point F, prove that :
(i) EF = FC
(ii) BF = DF

ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F. If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.
In cyclic quadrilateral ABCD; AD = BC, ∠BAC = 30° and ∠CBD = 70°; find :
(i) ∠BCD
(ii) ∠BCA
(iii) ∠ABC
(iv) ∠ADC
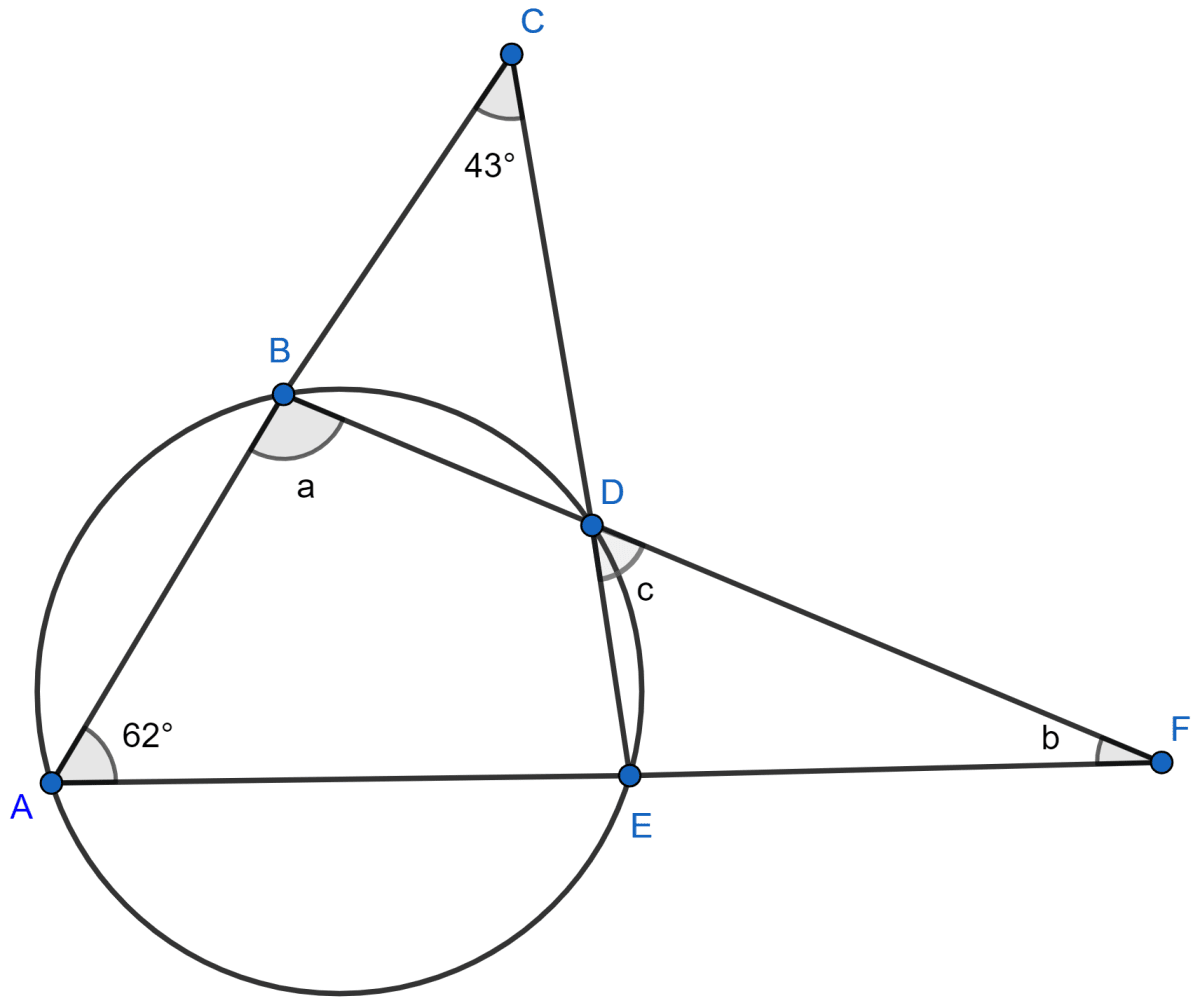
In the given figure, ∠ACE = 43° and ∠CAF = 62°; find the values of a, b and c.