ABCD is a cyclic quadrilateral. Sides AB and DC produced meet at point E; whereas sides BC and AD produced meet at point F. If ∠DCF : ∠F : ∠E = 3 : 5 : 4, find the angles of the cyclic quadrilateral ABCD.

Let ∠DCF = 3x, ∠F = 5x and ∠E = 4x.

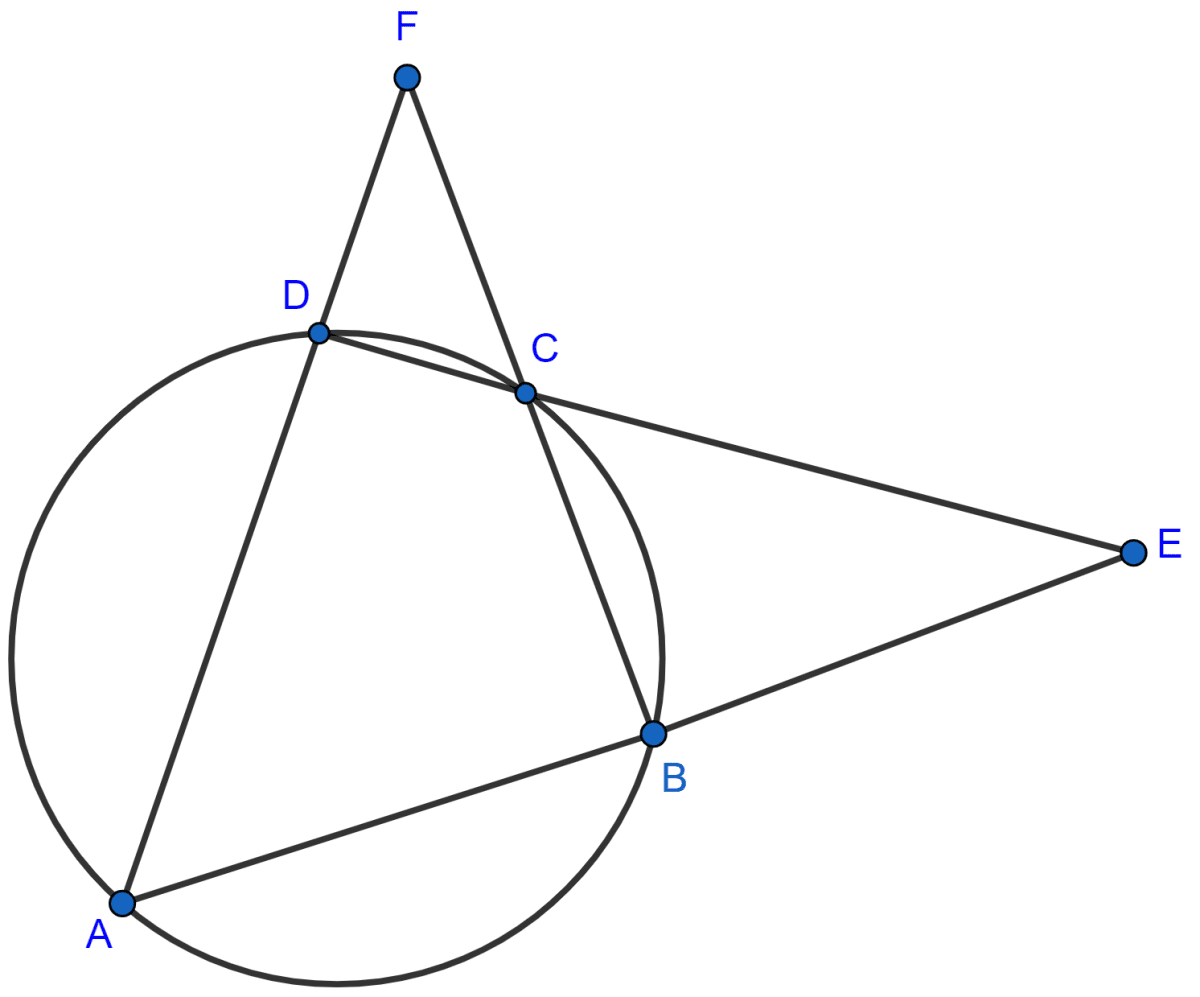
From figure,

⇒ ∠A + ∠DCB = 180° [As sum of opposite angles in a cyclic quadrilateral = 180°]

⇒ ∠A = 180° - ∠DCB

⇒ ∠A = 180° - (180° - ∠DCF) [As ∠DCF and DCB form a linear pair]

⇒ ∠A = ∠DCF = 3x.

In △CDF,

∠CDA = ∠F + ∠DCF [As exterior angle in a triangle is equal to sum of two opposite interior angles.]

= 5x + 3x = 8x

In △BCE,

⇒ ∠ABC = ∠BCE + ∠E [As exterior angle in a triangle is equal to sum of two opposite interior angles.]

⇒ ∠ABC = ∠DCF + ∠E [∠BCE = ∠DCF, Vertically opposite angles are equal]

⇒ ∠ABC = 3x + 4x = 7x.

In cyclic quadrilateral ABCD,

⇒ ∠ABC + ∠CDA = 180°

⇒ 7x + 8x = 180°

⇒ 15x = 180°

⇒ x = $\dfrac{180°}{15}$ = 12°.

∠A = 3x = 3 x 12° = 36°,

∠B = 7x = 7 x 12° = 84°,

∠C = 180° - ∠A = 180° - 36° = 144°,

∠D = 8x = 8 x 12° = 96°.

Hence, ∠A = 36°, ∠B = 84°, ∠C = 144°, ∠D = 96°.