Mathematics
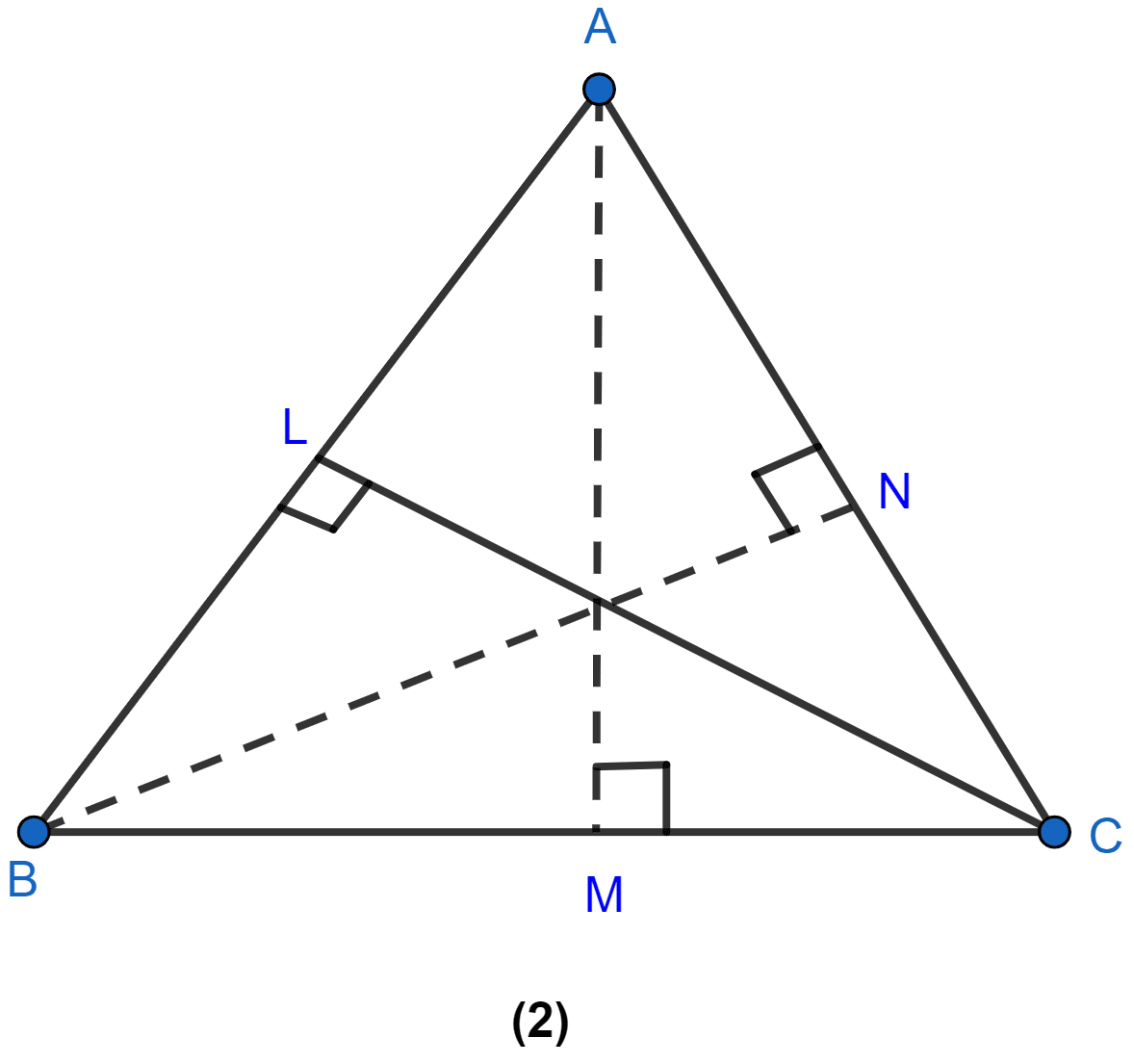
In the figure(3) given below, ABCD is a parallelogram. P is a point on DC such that area of ∆DAP = 25 cm2 and the area of ∆BCP = 15 cm2. Find
(i) area of || gm ABCD
(ii) DP : PC.
Theorems on Area
17 Likes
Answer
(i) Since,
∆APB and || gm ABCD have same base AB and are between same parallel lines AB and DC. So,
area of ∆APB = area of ||gm ABCD
From figure,
⇒ area of ||gm ABCD = area of (∆DAP + ∆BCP)
⇒ area of ||gm ABCD = 25 + 15 = 40
⇒ area of ||gm ABCD = 2 × 40 = 80 cm2.
Hence, area of ||gm ABCD = 80 cm2.
(ii) From figure,
∆DAP and ∆BCP are on the same base CD and between the same parallel lines CD and AB.
Hence, DP : PC = 5 : 3.
Answered By
13 Likes
Related Questions
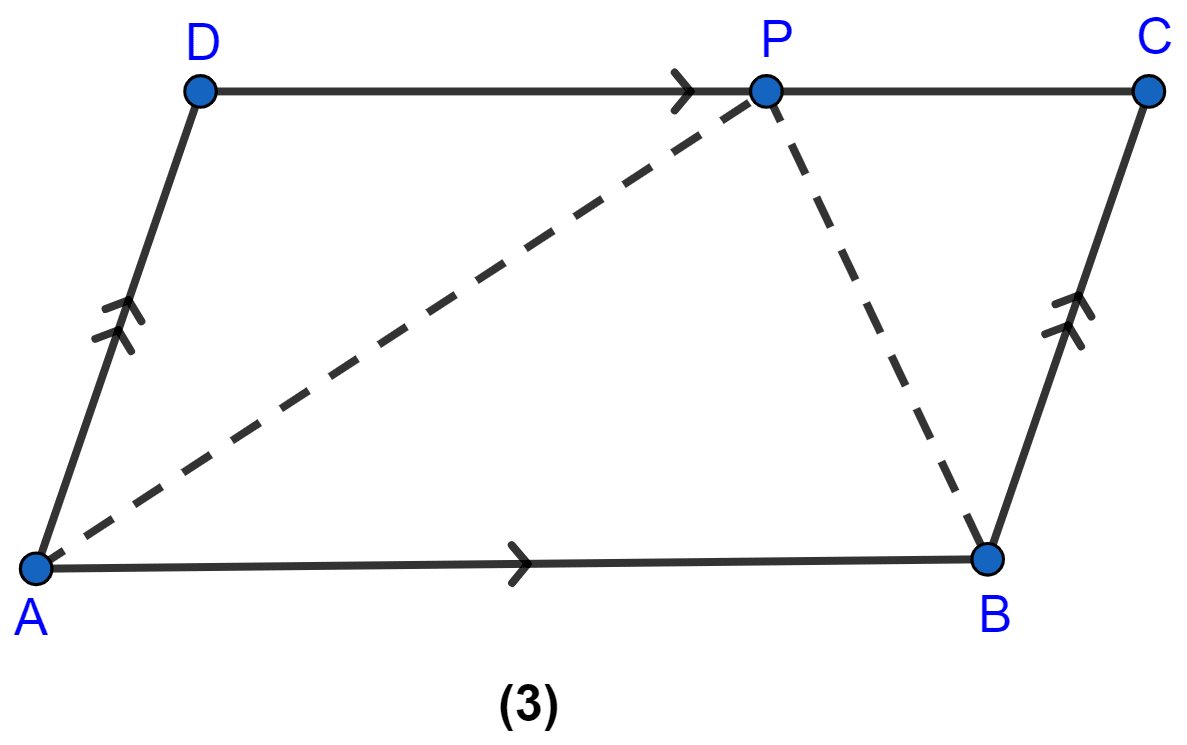
In the figure (2) given below, the perimeter of ∆ABC is 37 cm. If the lengths of the altitudes AM, BN and CL are 5x, 6x, and 4x respectively, calculate the lengths of the sides of ∆ABC.
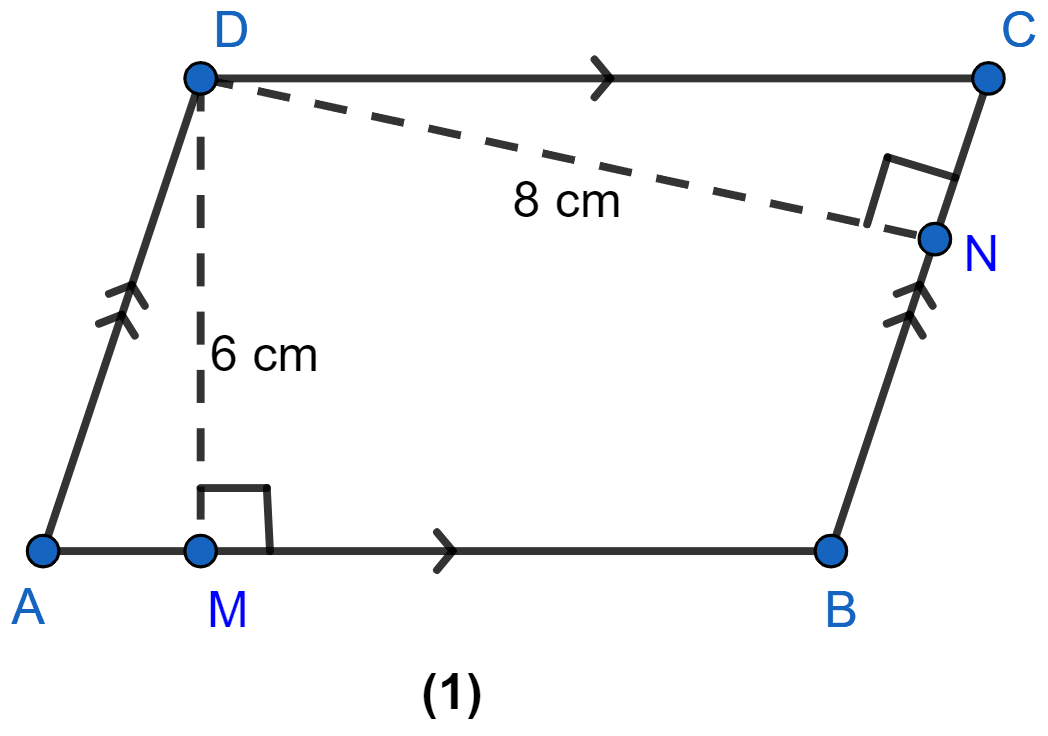
In figure (1) given below, the perimeter of the parallelogram is 42 cm. Calculate the lengths of the sides of the parallelogram.
In the adjoining figure, E is the midpoint of the side AB of a triangle ABC and EBCF is a parallelogram. If the area of ∆ ABC is 25 sq. units, find the area of || gm EBCF.
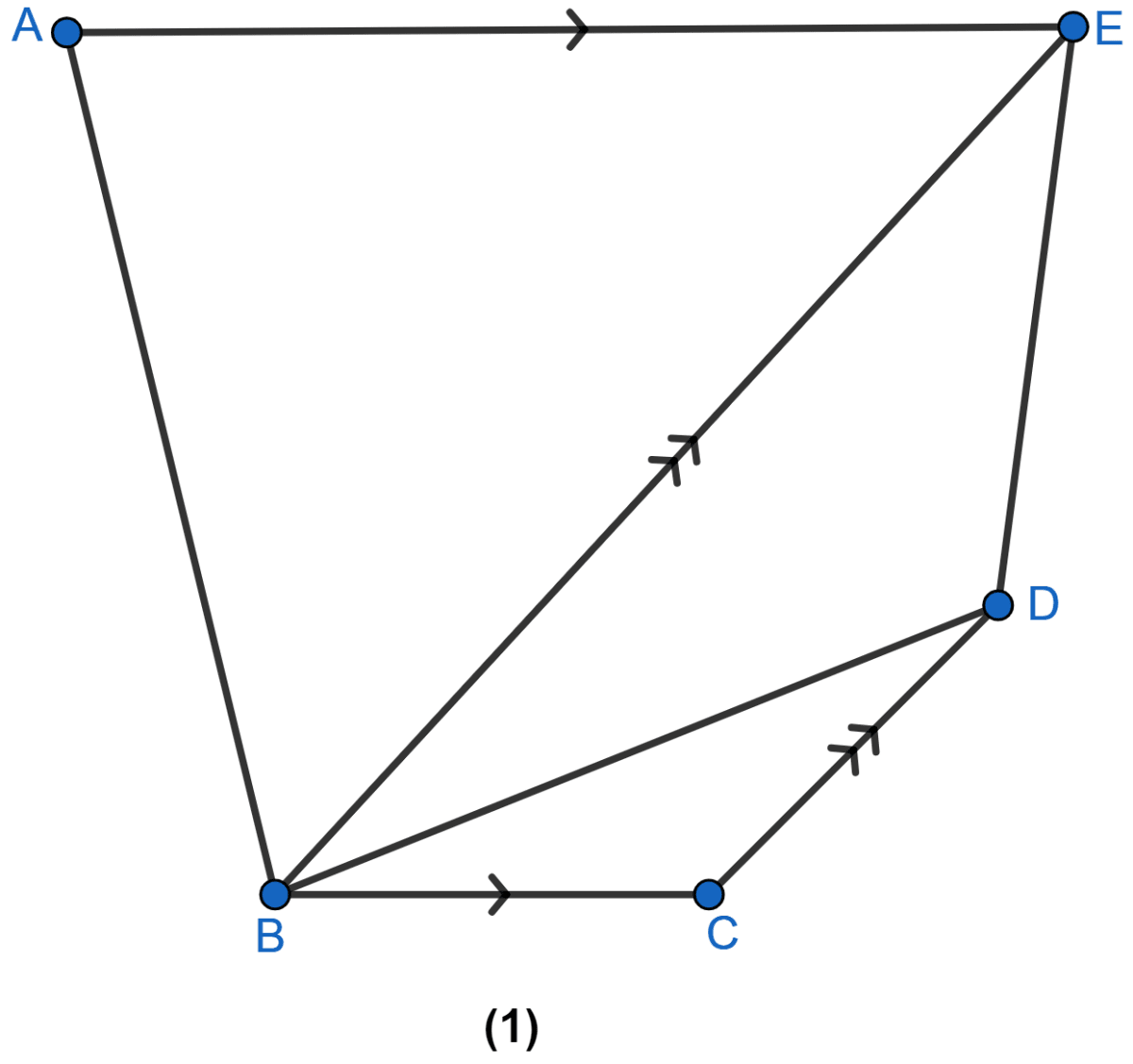
In the figure (1) given below, BC || AE and CD || BE. Prove that
area of ∆ABC= area of ∆EBD.