Mathematics
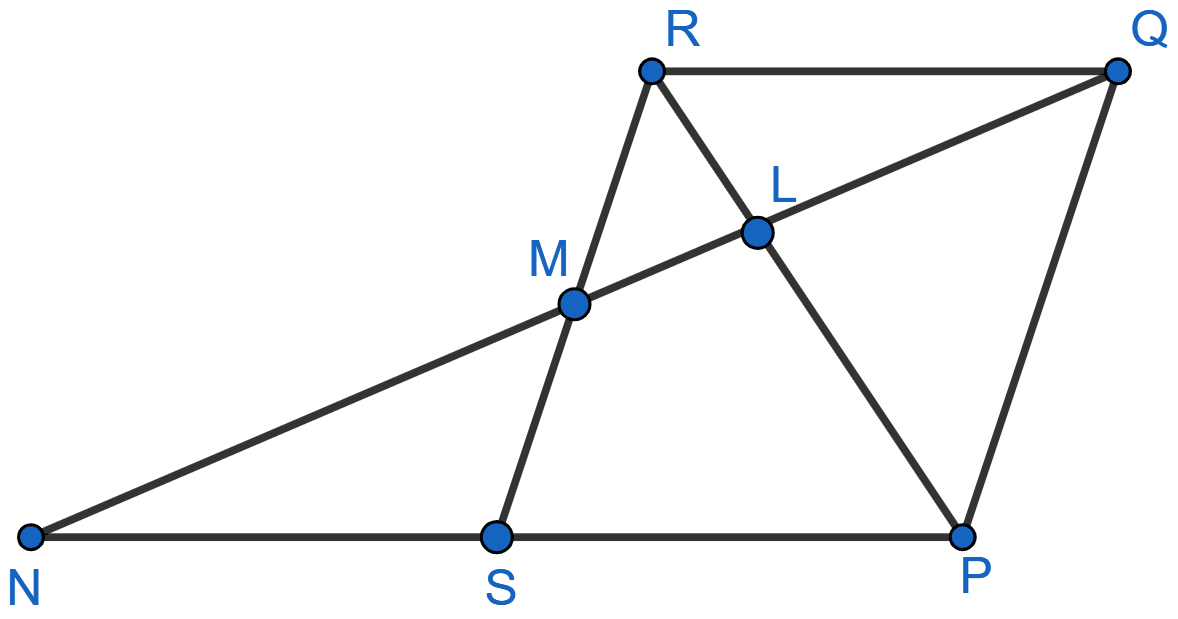
In the figure, PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm, L is a point on PR such that RL : LP = 2 : 3. QL produced meets RS at M and PS produced at N. Find the lengths of PN and RM.
Similarity
19 Likes
Answer
In △RLQ and △PLN,
⇒ ∠RLQ = ∠PLN [Vertically opposite angles are equal]
⇒ ∠LRQ = ∠LPN [Alternate angles are equal]
∴ △RLQ ~ △PLN [By AA]
Since, corresponding sides of similar triangles are proportional we have :
In △RLM and △PLQ,
⇒ ∠RLM = ∠PLQ [Vertically opposite angles are equal]
⇒ ∠LRM = ∠LPQ [Alternate angles are equal]
∴ △RLM ~ △PLQ [By AA]
Since, corresponding sides of similar triangles are proportional we have :
Hence, PN = 15 cm and RM = cm.
Answered By
11 Likes
Related Questions
In △PQR, ∠Q = 90° and QM is perpendicular to PR. Prove that :
(i) PQ2 = PM × PR
(ii) QR2 = PR × MR
(iii) PQ2 + QR2 = PR2
In △ABC, ∠B = 90° and BD ⊥ AC.
(i) If CD = 10 cm and BD = 8 cm; find AD.
(ii) If AC = 18 cm and AD = 6 cm; find BD.
(iii) If AC = 9 cm and AB = 7 cm; find AD.
In triangle ABC, AD is perpendicular to side BC and AD2 = BD × DC.
Show that angle BAC = 90°.
In the given figure, AB || EF || DC; AB = 67.5 cm, DC = 40.5 cm and AE = 52.5 cm.
(i) Name the three pairs of similar triangles.
(ii) Find the length of EC and EF.