Mathematics
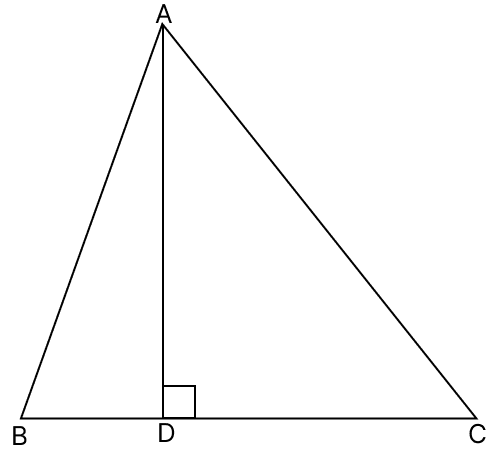
In triangle ABC, AD is perpendicular to side BC and AD2 = BD × CD.
prove that angle BAC = 90°.
Similarity
70 Likes
Answer
Triangle ABC is shown in the figure below:
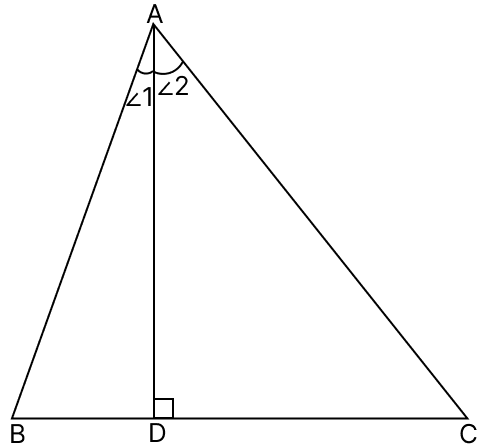
Given :
AD2 = BD × CD
⇒
∠ADB = ∠ADC [Both = 90°]
∴ △DBA ~ △DAC (By SAS).
Since, triangles are similar they will be equiangular.
∴ ∠1 = ∠C and ∠2 = ∠B
⇒ ∠1 + ∠2 = ∠B + ∠C
⇒ ∠A = ∠B + ∠C
By angle sum property :
⇒ ∠A + ∠B + ∠C = 180°
⇒ ∠A + ∠A = 180°
⇒ 2∠A = 180°
⇒ ∠A = 90°.
From figure,
⇒ ∠BAC = ∠A = 90°.
Hence, proved that ∠BAC = 90°.
Answered By
51 Likes
Related Questions
In triangle ABC and DEF, ∠A = ∠D and then prove that Δ ABC ∼ Δ DEF.
In triangle ABC and DEF, ∠A = ∠D, ∠B = ∠E and ∠C = ∠F. Also, AL and DM are medians. Prove that .
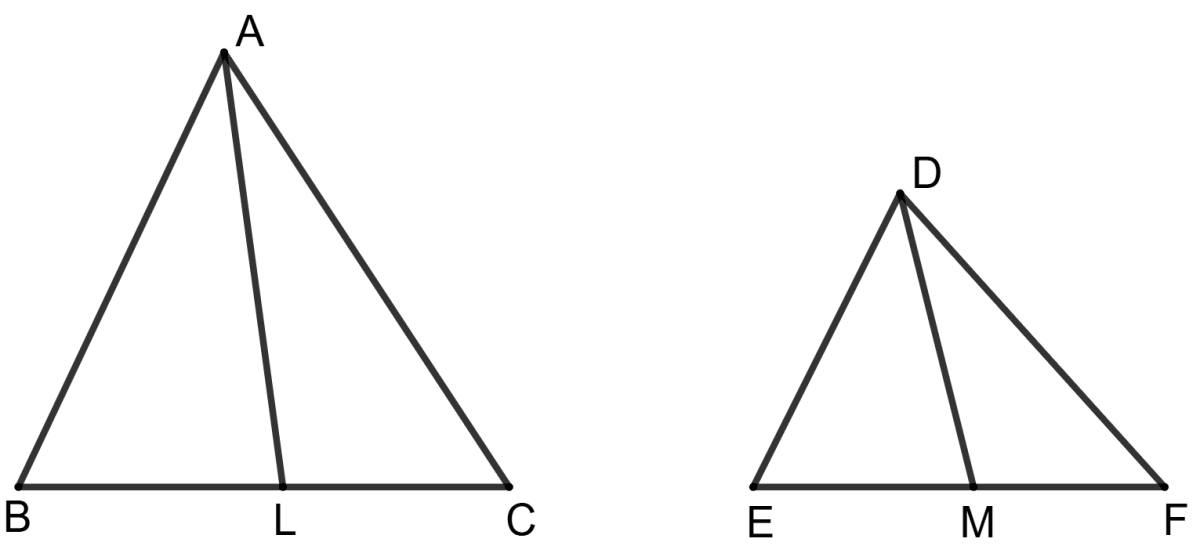
In the given figure, Δ ABC and Δ DEF are similar, BM and EN are their medians. If Δ ABC is similar to Δ DEF, prove that :
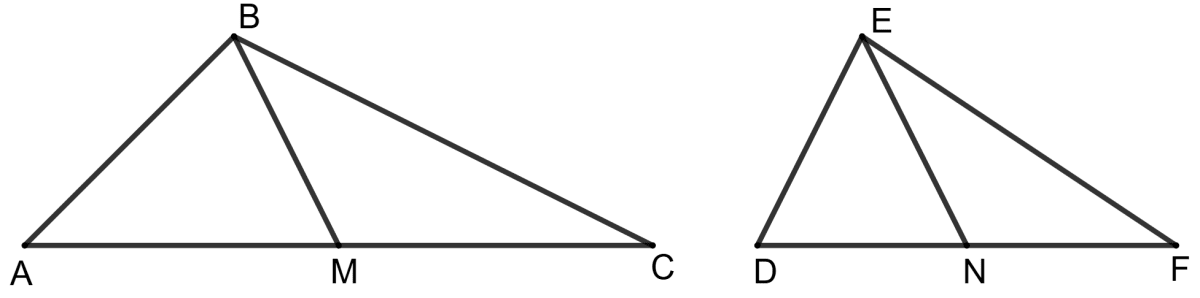
(i) Δ AMB ∼ Δ DNE
(ii) Δ CMB ∼ Δ FNE
(iii)
In the given figure, Δ ABC is isosceles and AP x BQ = AC2, prove that Δ ACP ∼ Δ BCQ.