Mathematics
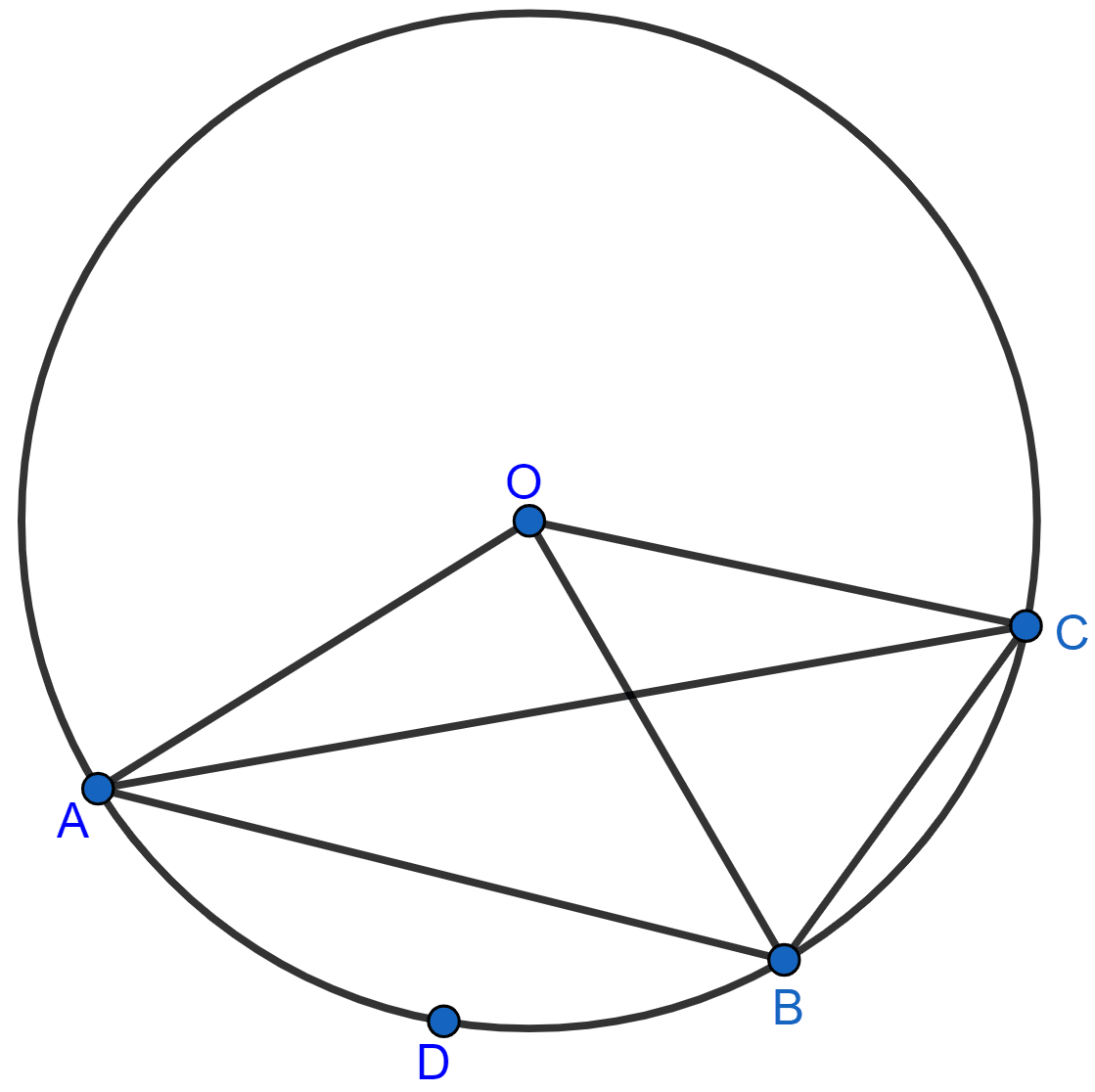
In the figure, O is the centre of the circle and the length of arc AB is twice the length of arc BC. If angle AOB = 108°, find :
(i) ∠CAB,
(ii) ∠ADB.
Circles
25 Likes
Answer
Join AD and BD.
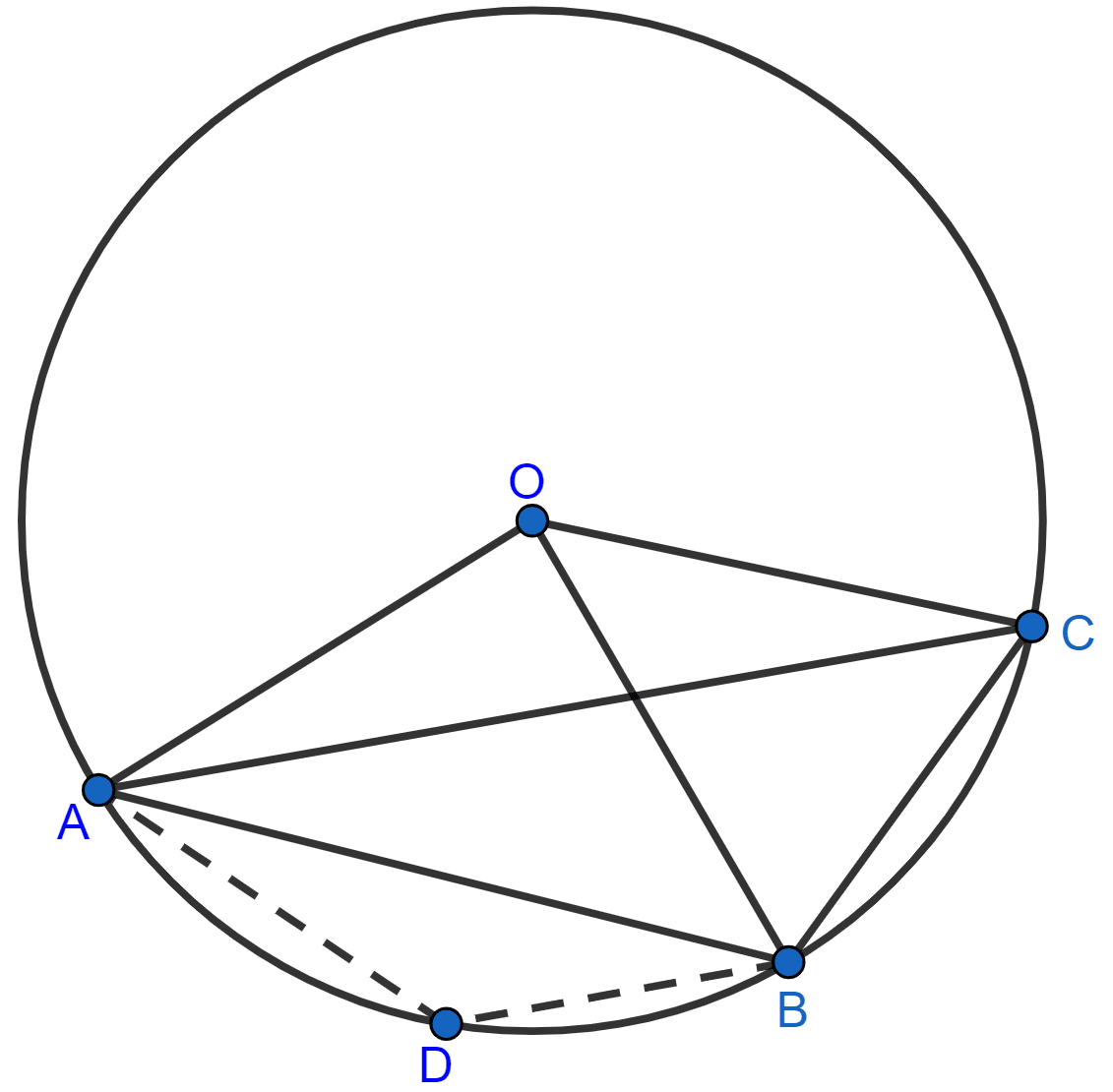
(i) Given,
⇒ arc AB = 2 arc BC
⇒ ∠AOB = 2∠BOC
⇒ ∠BOC = ∠AOB = = 54°.
We know that,
Angle which an arc subtends at the center is double that which it subtends at any point on the remaining part of the circumference.
∴ ∠BOC = 2∠CAB
⇒ ∠CAB = ∠BOC = = 27°.
Hence, ∠CAB = 27°.
(ii) Arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.
∴ ∠AOB = 2∠ACB
∠ACB = ∠AOB = = 54°.
In cyclic quadrilateral ADBC,
⇒ ∠ADB + ∠ACB = 180° [As sum of opposite angles in cyclic quadrilateral = 180°]
⇒ ∠ADB + 54° = 180°
⇒ ∠ADB = 180° - 54° = 126°.
Hence, ∠ADB = 126°.
Answered By
18 Likes
Related Questions
In a regular pentagon ABCDE, inscribed in a circle; find the ratio between angle EDA and angle ADC.
In the given figure, AB = BC = CD and ∠ABC = 132°. Calculate :
(i) ∠AEB,
(ii) ∠AED,
(iii) ∠COD.

The figure shows a circle with centre O. AB is the side of regular pentagon and AC is the side of regular hexagon.
Find the angles of triangle ABC.

In the given figure, BD is a side of regular hexagon, DC is a side of a regular pentagon and AD is a diameter. Calculate :
(i) ∠ADC,
(ii) ∠BDA,
(iii) ∠ABC,
(iv) ∠AEC.