Mathematics
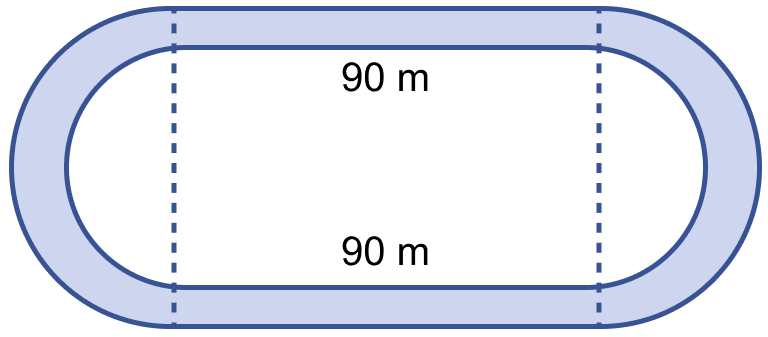
In the figure (ii) given below, the inside perimeter of a practice running track with semi-circular ends and straight parallel sides is 312 m. The length of the straight portion of the track is 90 m. If the track has a uniform width of 2 m throughout, find its area.
Mensuration
29 Likes
Answer
Given,
Perimeter of inside semi-circular track = 312 m.
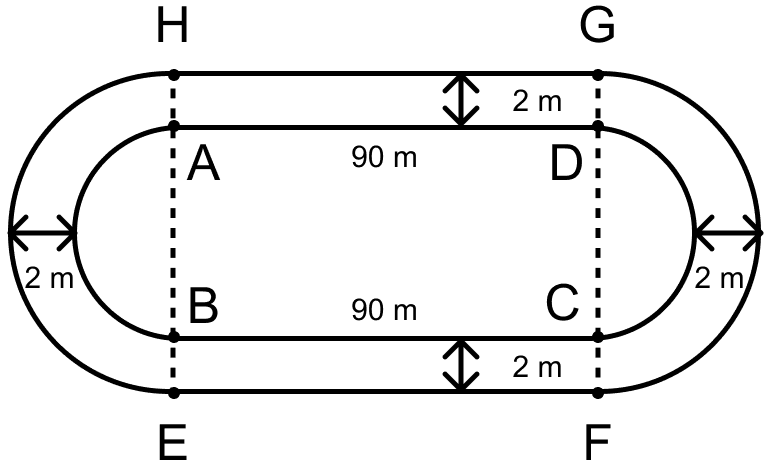
⇒ 90 + πr + 90 + πr = 312
⇒ 2πr + 180 = 312
⇒ 2πr = 312 - 180
⇒ 2πr = 132
⇒ πr =
⇒ πr = 66
⇒ r = m.
So, length of AB = 2r = 2 × 21 = 42 m.
Since, width of track = 2 m.
So, HE = GF = 42 + 2 + 2 = 46 m.
Radius of outer semi-circle (R) = = 23 m.
From figure,
Area of track = Area of outer semi-circle (with diametre HE) + Area of outer semi-circle( with diametre GF) + Area of outer rectangle (EFGH) - [Area of inner semi-circle (with diameter AB) + Area of inner semi-circle (with diameter DC) + Area of inner rectangle ABCD]
Hence, area of semi-circular track = m2.
Answered By
17 Likes
Related Questions
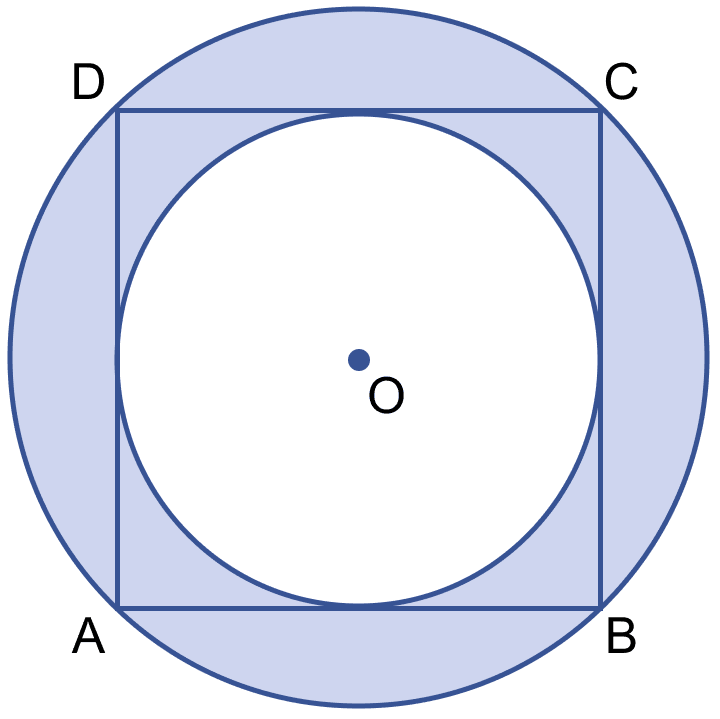
In the adjoining figure, ABCD is a square. Find the ratio between
(i) the circumferences
(ii) the areas of the incircle and the circumcircle of the square.
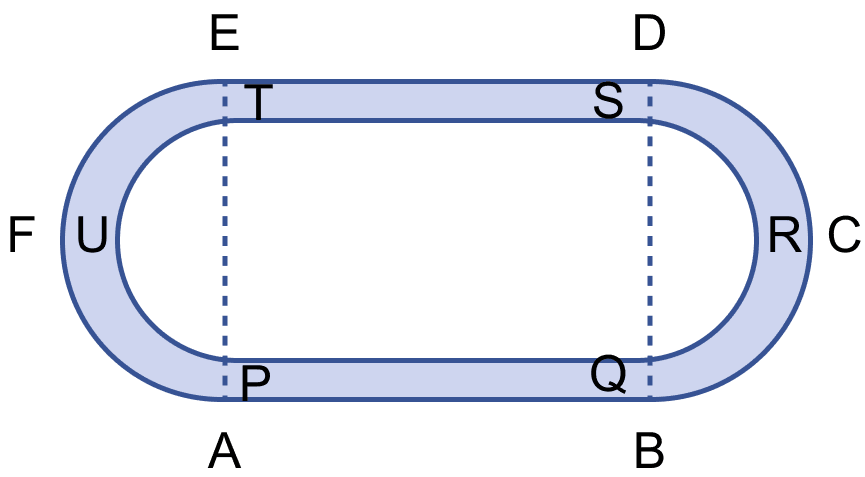
The figure (i) given below shows a running track surrounding a grassed enclosure PQRSTU. The enclosure consists of a rectangle PQST with a semicircular region at each end. PQ = 200 m; PT = 70 m.
(i) Calculate the area of the grassed enclosure in m2.
(ii) Given that the track is of constant width 7 m, calculate the outer perimeter ABCDEF of the track.
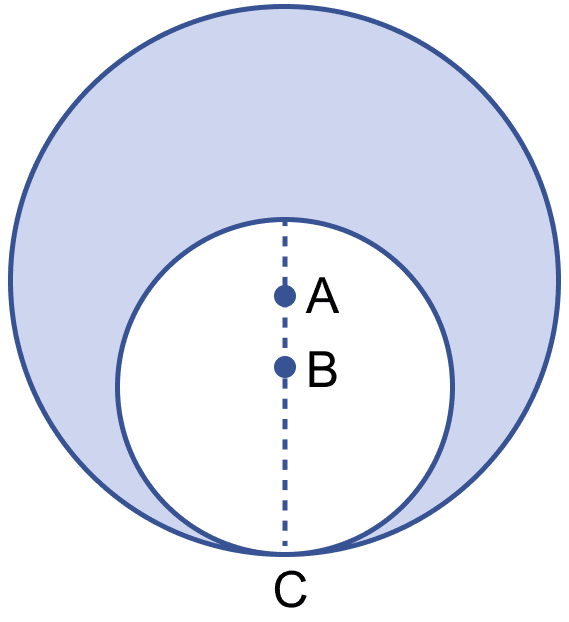
In the figure (i) given below, two circles with centres A and B touch each other at the point C. If AC = 8 cm and AB = 3 cm, find the area of the shaded region.
The quadrants shown in the figure (ii) given below are each of radius 7 cm. Calculate the area of the shaded portion.
