Mathematics
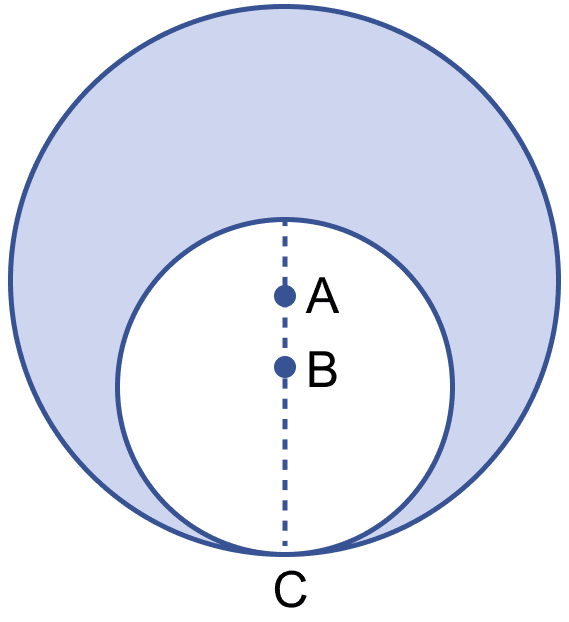
In the figure (i) given below, two circles with centres A and B touch each other at the point C. If AC = 8 cm and AB = 3 cm, find the area of the shaded region.
Mensuration
20 Likes
Answer
Radius of circle with center A = AC = 8 cm.
Area of circle with center A = πr2
=
= = 201.14 cm2.
From figure,
BC = AC - AB = 8 - 3 = 5 cm.
Area of circle with center B = πr2
=
= = 78.57 cm2.
Area of shaded region = Area of circle with center A - Area of circle with center B
= 201.14 - 78.57
= 122.57 cm2.
Hence, area of shaded region = 122.57 cm2.
Answered By
12 Likes
Related Questions
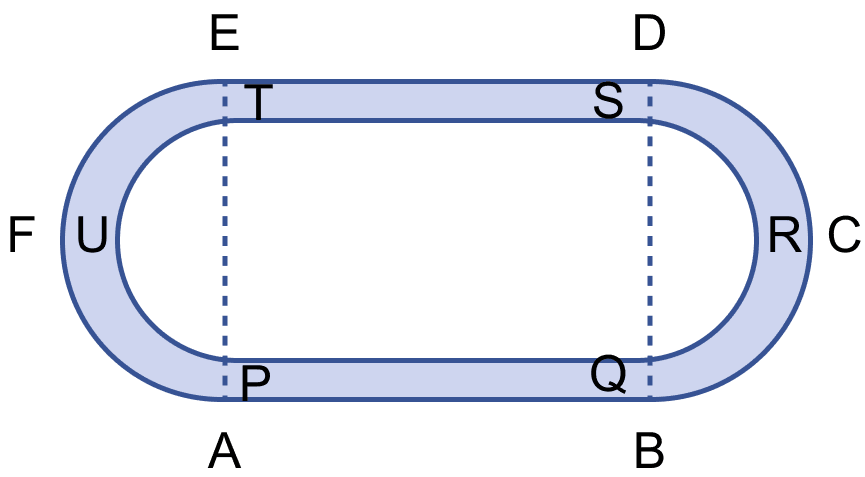
The figure (i) given below shows a running track surrounding a grassed enclosure PQRSTU. The enclosure consists of a rectangle PQST with a semicircular region at each end. PQ = 200 m; PT = 70 m.
(i) Calculate the area of the grassed enclosure in m2.
(ii) Given that the track is of constant width 7 m, calculate the outer perimeter ABCDEF of the track.
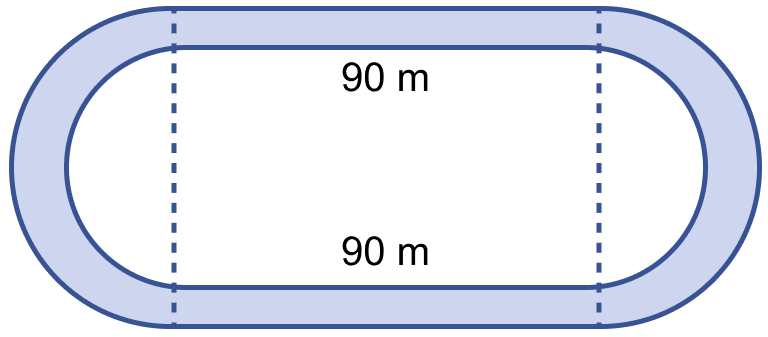
In the figure (ii) given below, the inside perimeter of a practice running track with semi-circular ends and straight parallel sides is 312 m. The length of the straight portion of the track is 90 m. If the track has a uniform width of 2 m throughout, find its area.
The quadrants shown in the figure (ii) given below are each of radius 7 cm. Calculate the area of the shaded portion.

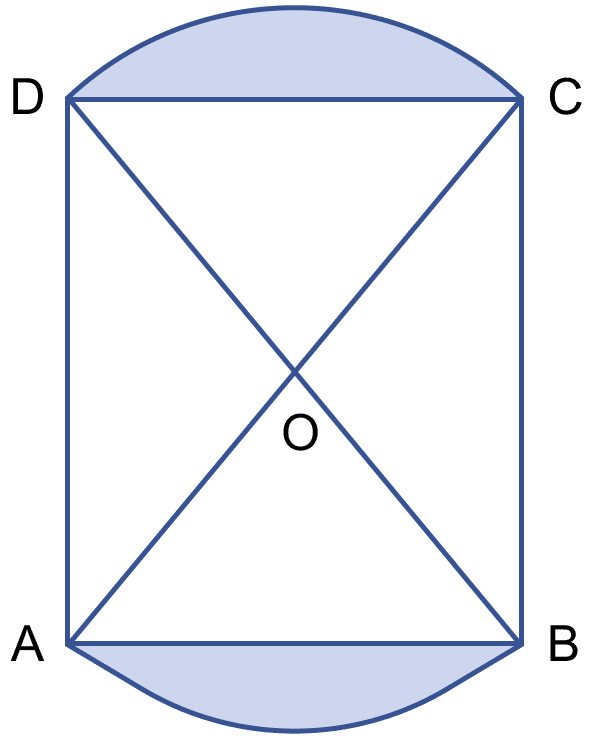
In the figure (i) given below, two circular flower beds have been shown on the two sides of a square lawn ABCD of side 56 m. If the centre of each circular flower bed is the point of intersection O of the diagonals of the square lawn, find the sum of the areas of the lawn and the flower beds.