Mathematics
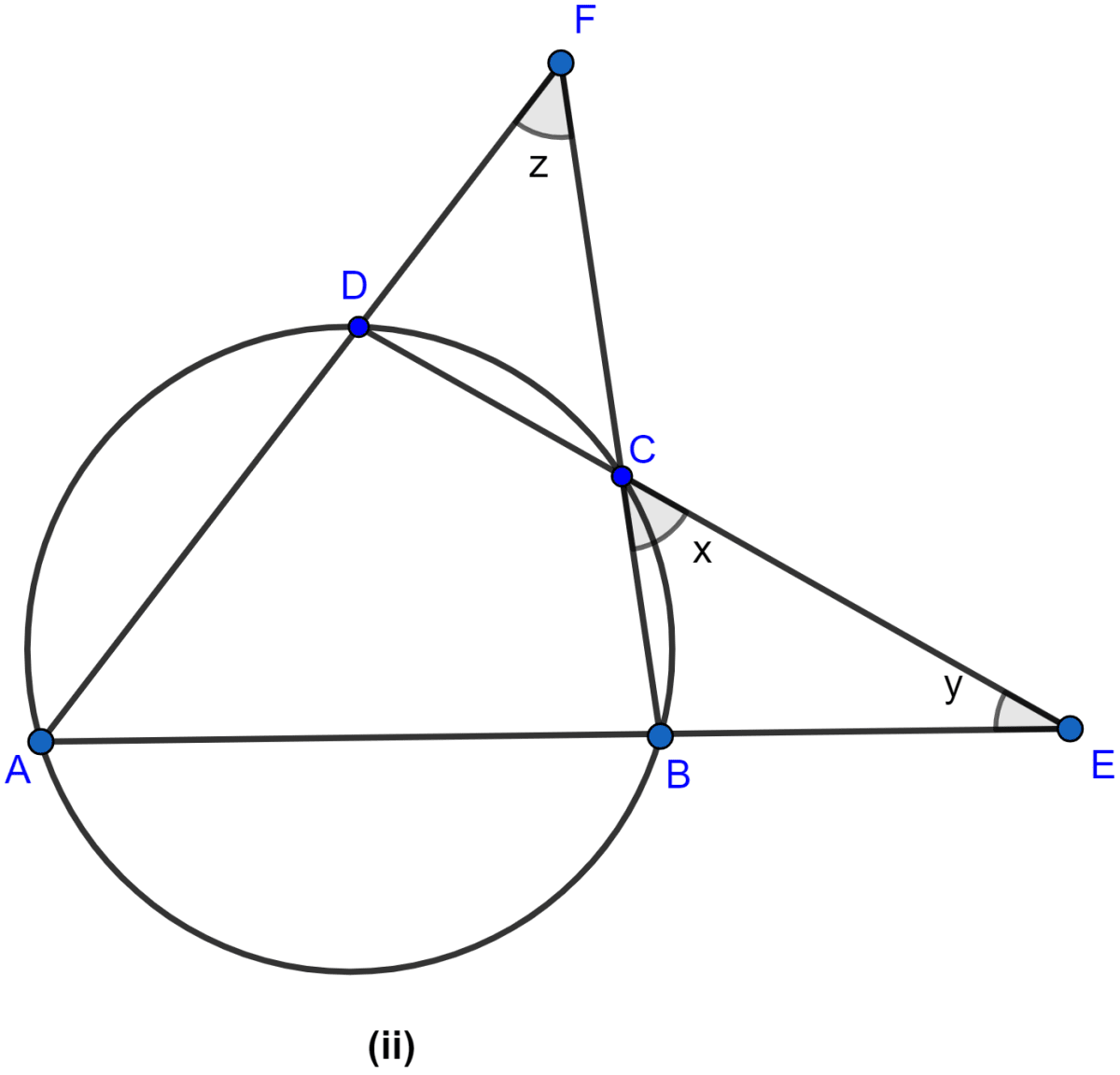
In the figure (ii) given below, sides AB and DC of a cyclic quadrilateral ABCD are produced to meet at E, the sides AD and BC are produced to meet at F. If x : y : z = 3 : 4 : 5, find the values of x, y and z.
Circles
76 Likes
Answer
In figure,
ABCD is a cyclic quadrilateral.
∠DAB = ∠BCE = x (Property of cyclic quadrilateral by which an exterior angle = opposite interior angle.)
In △BCE
∠CBE = 180° - (x° + y°)
From figure,
∠CBE and ∠CBA are linear pairs.
So,
⇒ ∠CBE + ∠CBA = 180°
⇒ 180° - (x° + y°) + ∠CBA = 180°
⇒ ∠CBA = 180° - 180° + (x° + y°)
⇒ ∠CBA = x° + y°
In △ABF,
So,
∠BAF + ∠ABF + ∠AFB = 180°
x + (x + y) + z = 180° (∵ From figure, ∠BAF = ∠DAB and ∠ABF = ∠CBA)
Given x : y : z = 3 : 4 : 5 , so x = 3k, y = 4k and z = 5k
3k + (3k + 4k) + 5k = 180°
15k = 180°
k = 12°
Hence, x = 3k = 3 × 12° = 36°, y = 4k = 4 × 12° = 48° and z = 5k = 5 × 12° = 60°.
Hence, the value of x = 36°, y = 48° and z = 60°.
Answered By
51 Likes
Related Questions
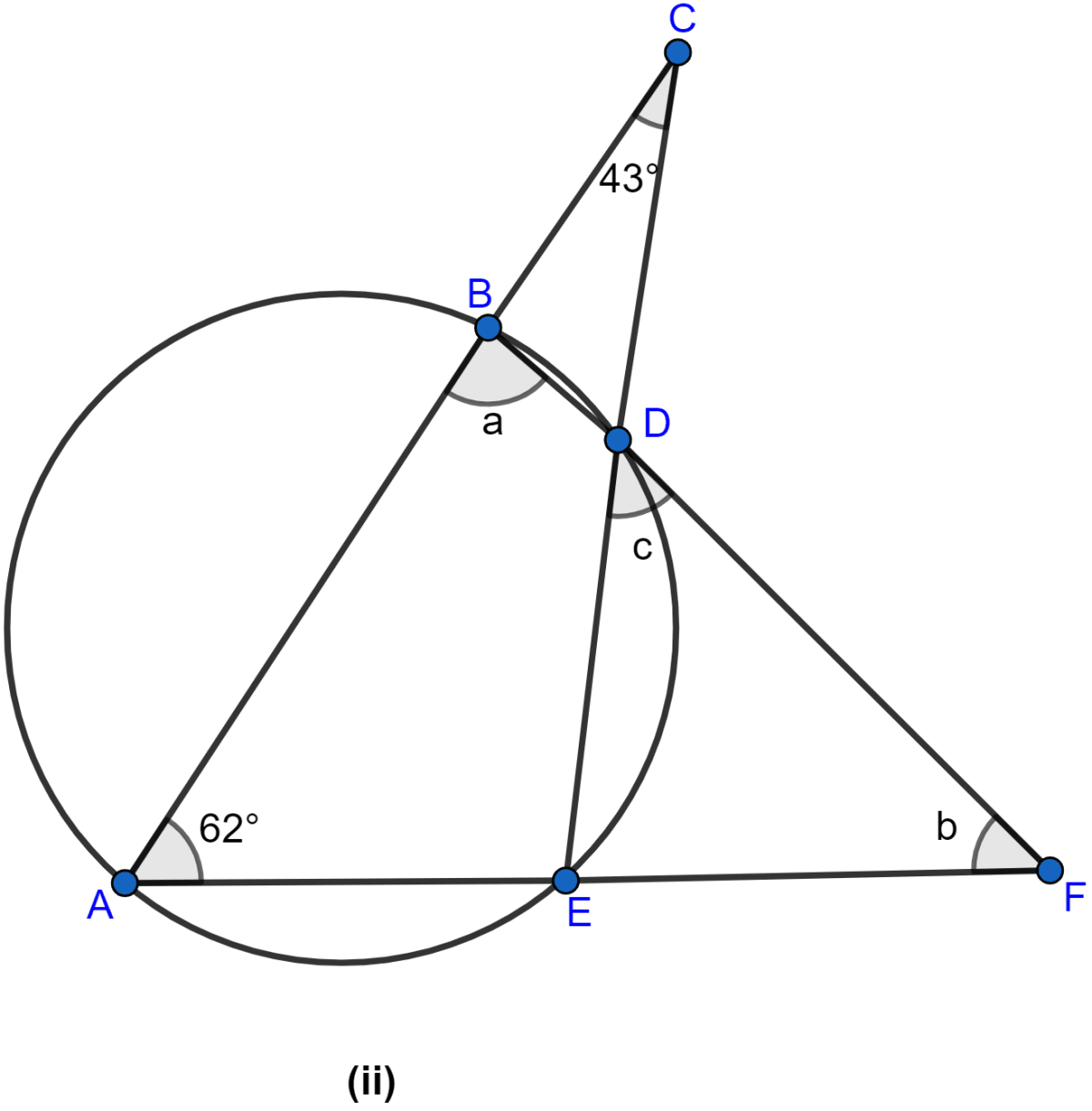
In the figure (ii) given below, if ∠ACE = 43° and ∠CAF = 62°, find the values of a, b and c.
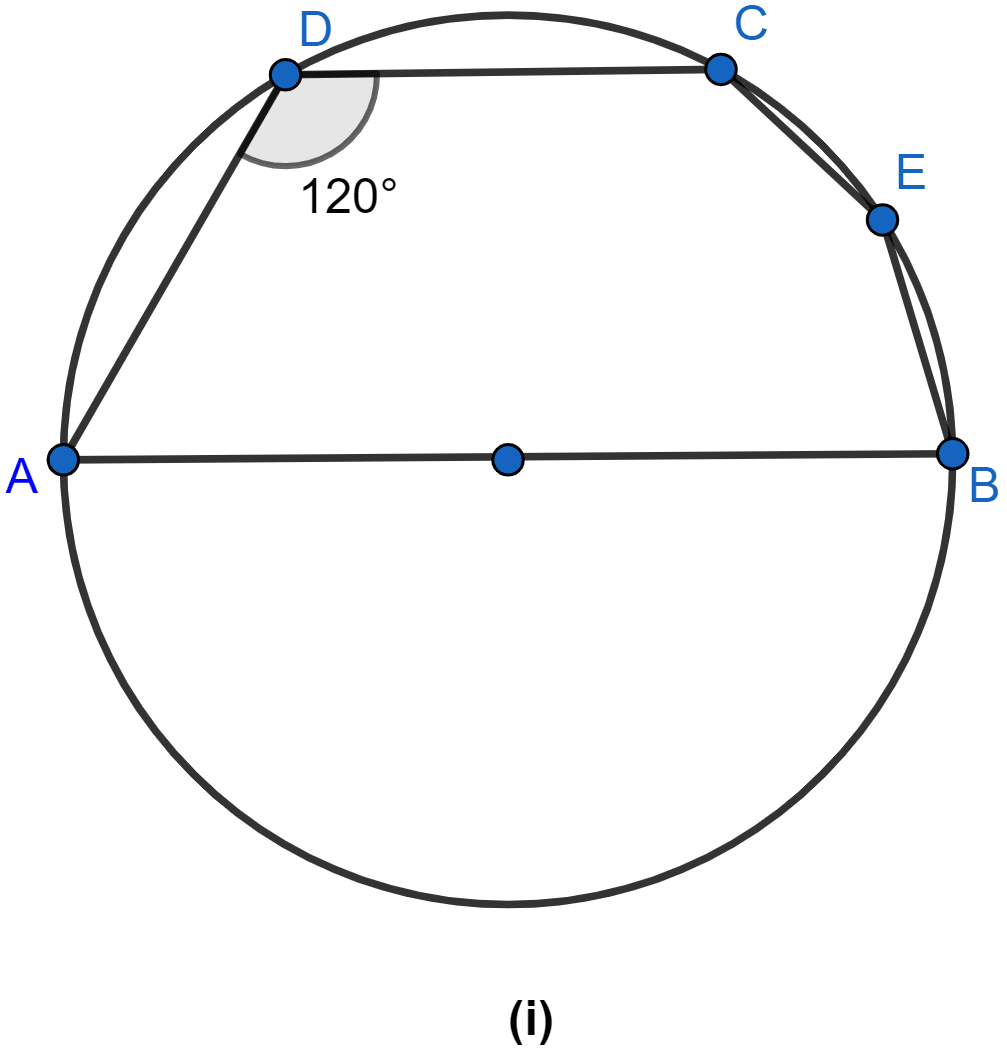
In the figure (i) given below, AB is a diameter of the circle. If ∠ADC = 120°, find ∠CAB.
In the figure (i) given below, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E. If ∠ADE = 70° and ∠OBA = 45°, calculate
(i) ∠OCA
(ii) ∠BAC
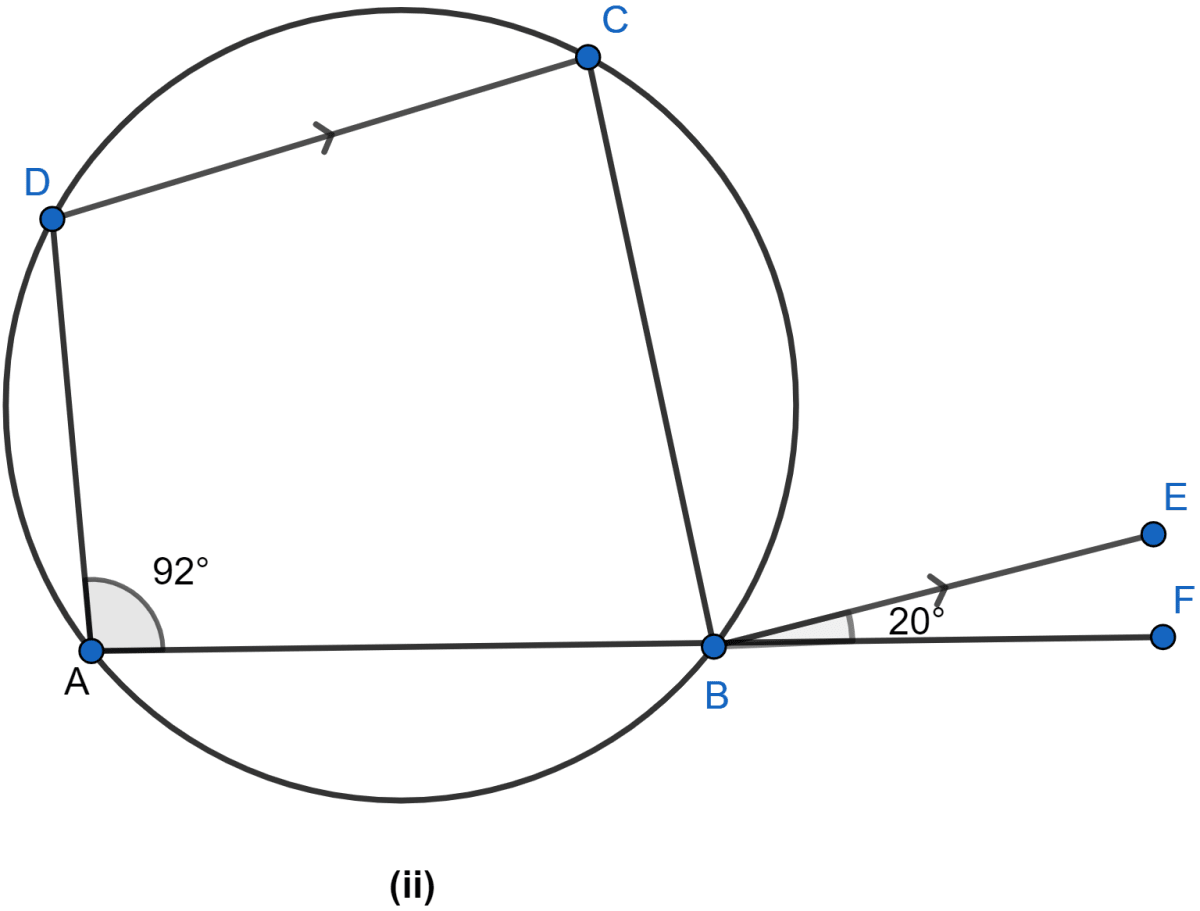
In figure (ii) given below, ABF is a straight line and BE || DC. If ∠DAB = 92° and ∠EBF = 20°, find
(i) ∠BCD
(ii) ∠ADC