KnowledgeBoat Logo

Mathematics

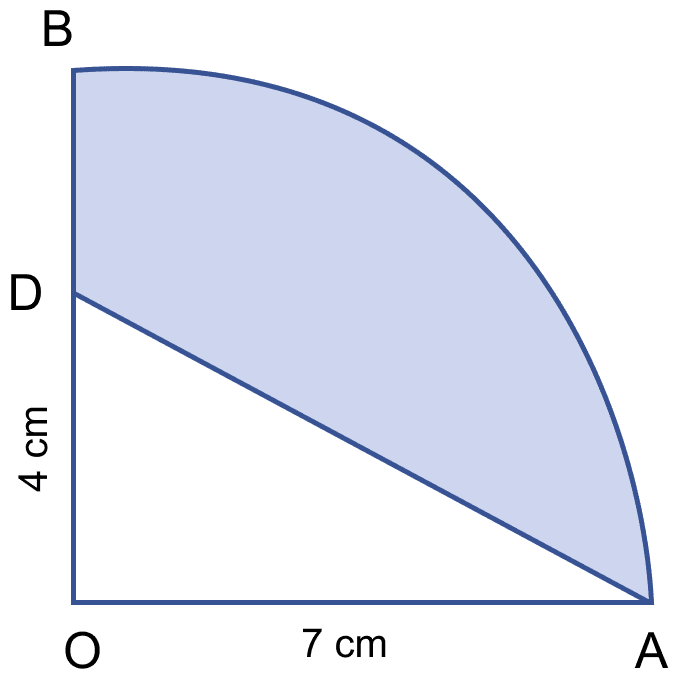
In the figure (ii) given below, OAB is a quadrant of a circle. The radius OA = 7 cm and OD = 4 cm. Calculate the area of the shaded portion.

In the figure, OAB is a quadrant of a circle. The radius OA = 7 cm and OD = 4 cm. Calculate the area of the shaded portion. Mensuration, ML Aggarwal Understanding Mathematics Solutions ICSE Class 9.

Mensuration

9 Likes

Answer

Area of quadrant = πr24\dfrac{πr^2}{4}

=227×724=1544=38.5 cm2.= \dfrac{\dfrac{22}{7} \times 7^2}{4} \\[1em] = \dfrac{154}{4} \\[1em] = 38.5 \text{ cm}^2.

Area of triangle AOD = 12×OA×OD\dfrac{1}{2} \times OA \times OD

=12×7×4=12×28=14 cm2= \dfrac{1}{2} \times 7 \times 4 \\[1em] = \dfrac{1}{2} \times 28 \\[1em] = 14 \text{ cm}^2

Area of shaded region = Area of quadrant - Area of triangle

= 38.5 - 14

= 24.5 cm2.

Hence, area of shaded region = 24.5 cm2.

Answered By

5 Likes

Related Questions