Mathematics
Answer
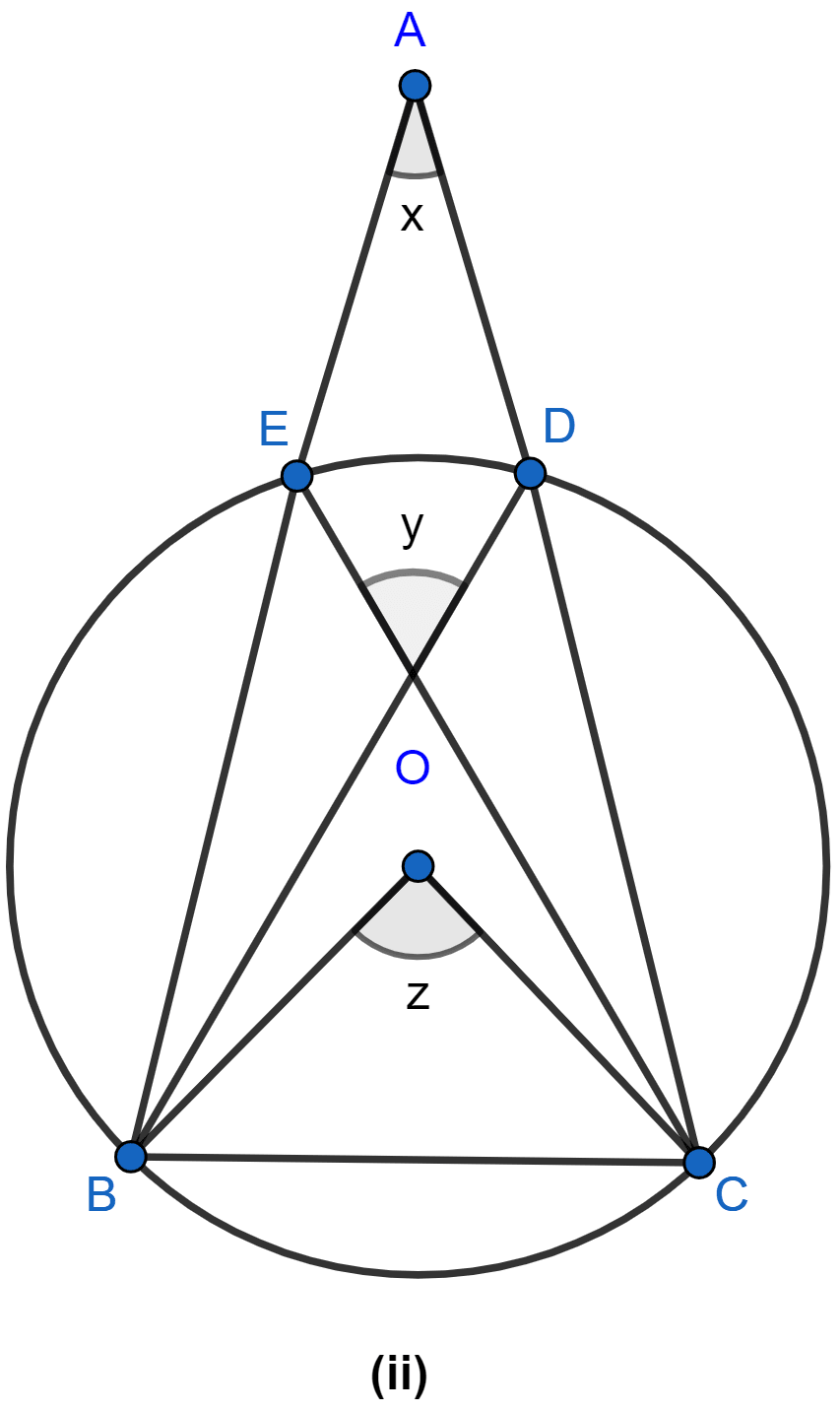
From figure,
∠BEC = ∠BDC (∵ angles in same segment are equal)
Arc BC subtends ∠BOC at the centre and ∠BEC at the remaining part of the circle.
∴ ∠BOC = 2∠BEC (∵ angle subtended on centre is double the angle subtended at remaining part of the circle.)
⇒ ∠BOC = ∠BEC + ∠BEC = ∠BEC + ∠BDC
⇒ ∠BOC = ∠BEC + ∠BDC …..(i)
In △OBE,
⇒ ∠EOD = ∠EBO + ∠BEO ….(ii) (∵ exterior angle is equal to the sum of two opposite interior angles.)
From figure,
∠EBO = ∠EBD and ∠BEO = ∠BEC and Exterior angle ∠EOD = y.
Putting these values in eqn (ii) we get,
⇒ y = ∠EBD + ∠BEC
⇒ ∠BEC = y - ∠EBD …..(iii)
In △ABD,
∠BDC = ∠BAD + ∠ABD ….(iv) (∵ exterior angle is equal to the sum of two opposite interior angles.)
From figure,
∠ABD = ∠EBD and ∠BAD = x.
Putting these values in eqn (iv) we get,
∠BDC = x + ∠EBD ……(v)
Putting value of ∠BEC and ∠BDC from eqn (iii) and (v) respectively in (i) we get,
⇒ ∠BOC = ∠BEC + ∠BDC
⇒ ∠BOC = y - ∠EBD + x + ∠EBD
⇒ ∠BOC = x + y
From figure,
∠BOC = z.
∴ z = x + y.
Hence, proved that x + y = z.
Related Questions
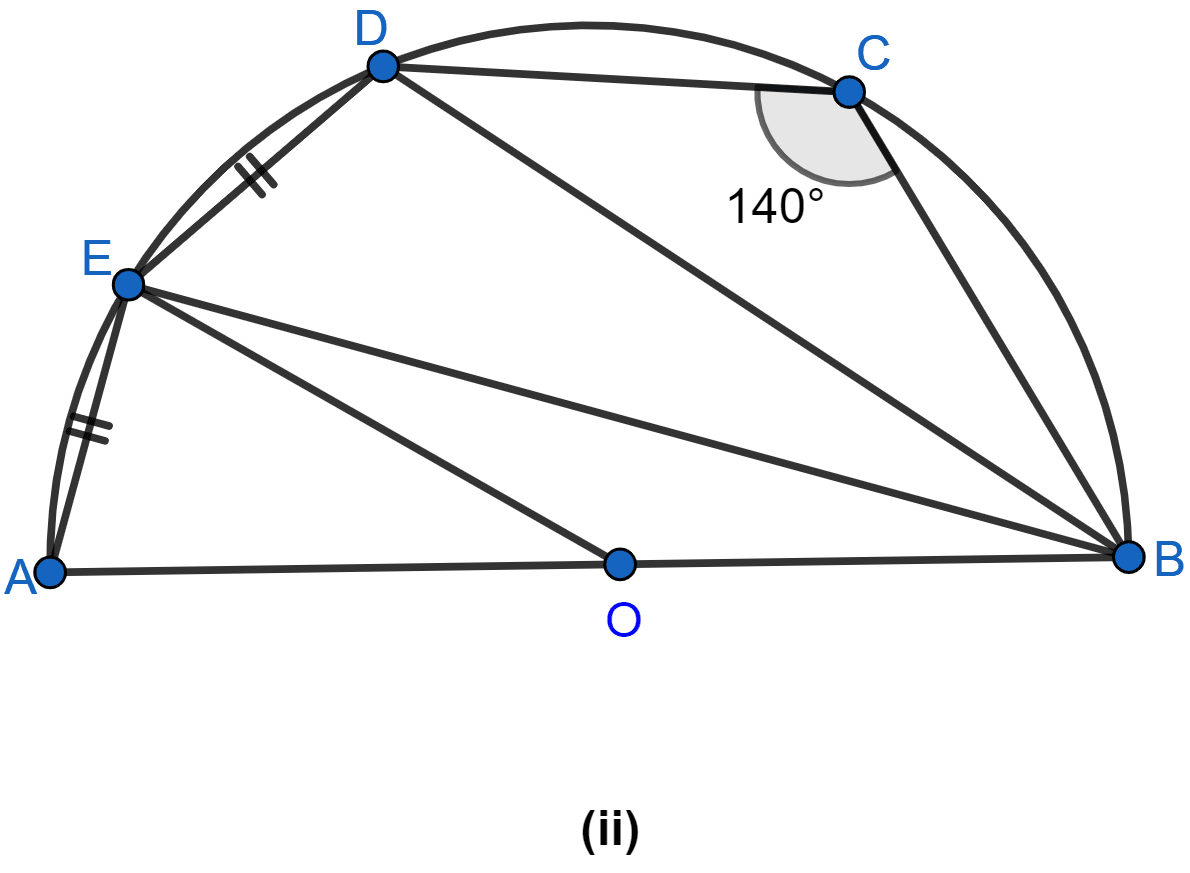
In the figure (ii) given below, AB is a diameter of the semicircle ABCDE with centre O. If AE = ED and ∠BCD = 140°, find ∠AED and ∠EBD. Also prove that OE is parallel to BD.
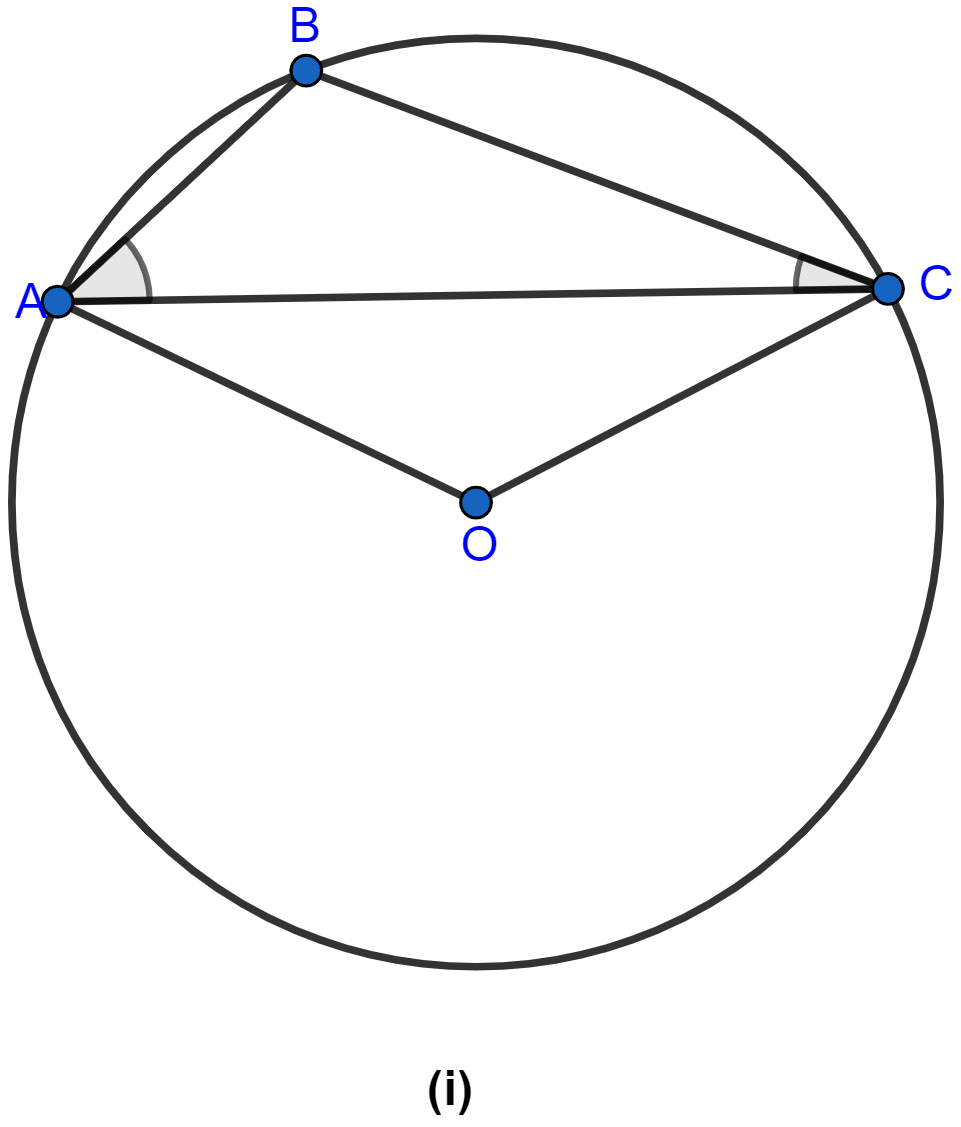
In the figure (i) given below, O is the centre of the circle. Prove that ∠AOC = 2(∠ACB + ∠BAC).
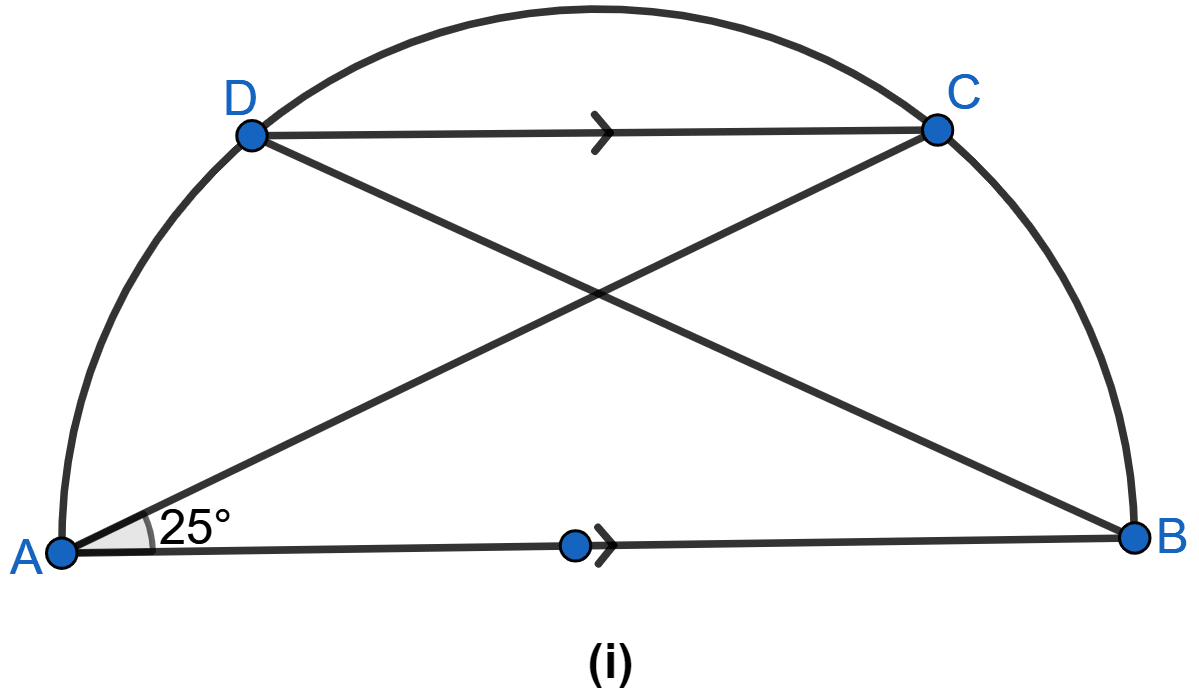
In the figure (i) given below, AB is diameter of a circle. If DC is parallel to AB and ∠CAB = 25°, find (i) ∠ADC (ii) ∠DAC.
In the figure (ii) given below, sides AB and DC of a cyclic quadrilateral are produced to meet at a point P and the sides AD and BC produced to meet at a point Q. If ∠ADC = 75° and ∠BPC = 50°, find ∠BAD and ∠CQD.