Mathematics
In the figure (ii) given below, sides AB and DC of a cyclic quadrilateral are produced to meet at a point P and the sides AD and BC produced to meet at a point Q. If ∠ADC = 75° and ∠BPC = 50°, find ∠BAD and ∠CQD.

Circles
14 Likes
Answer
Since sum of angles in a triangle = 180°.
In △ADP,
⇒ ∠ADP + ∠DAP + ∠DPA = 180°
⇒ 75° + ∠DAP + 50° = 180°
⇒ ∠DAP + 125° = 180°
⇒ ∠DAP = 180° - 125° = 55°.
From figure,
∠BAD = ∠DAP = 55°.
In cyclic quadrilateral sum of opposite angles = 180°
In ABCD,
∴ ∠ADC + ∠CBA = 180°
⇒ 75° + ∠CBA = 180°
⇒ ∠CBA = 180° - 75° = 105°.
In △ABQ,
⇒ ∠ABQ + ∠BAQ + ∠AQB = 180°
From figure, ∠BAQ = ∠BAD and ∠ABQ = ∠CBA or,
⇒ 105° + 55° + ∠AQB = 180°
⇒ ∠AQB + 160° = 180°
⇒ ∠AQB = 180° - 160° = 20°.
From figure,
∠CQD = ∠AQB = 20°.
Hence, the value of ∠BAD = 55° and ∠CQD = 20°.
Answered By
8 Likes
Related Questions
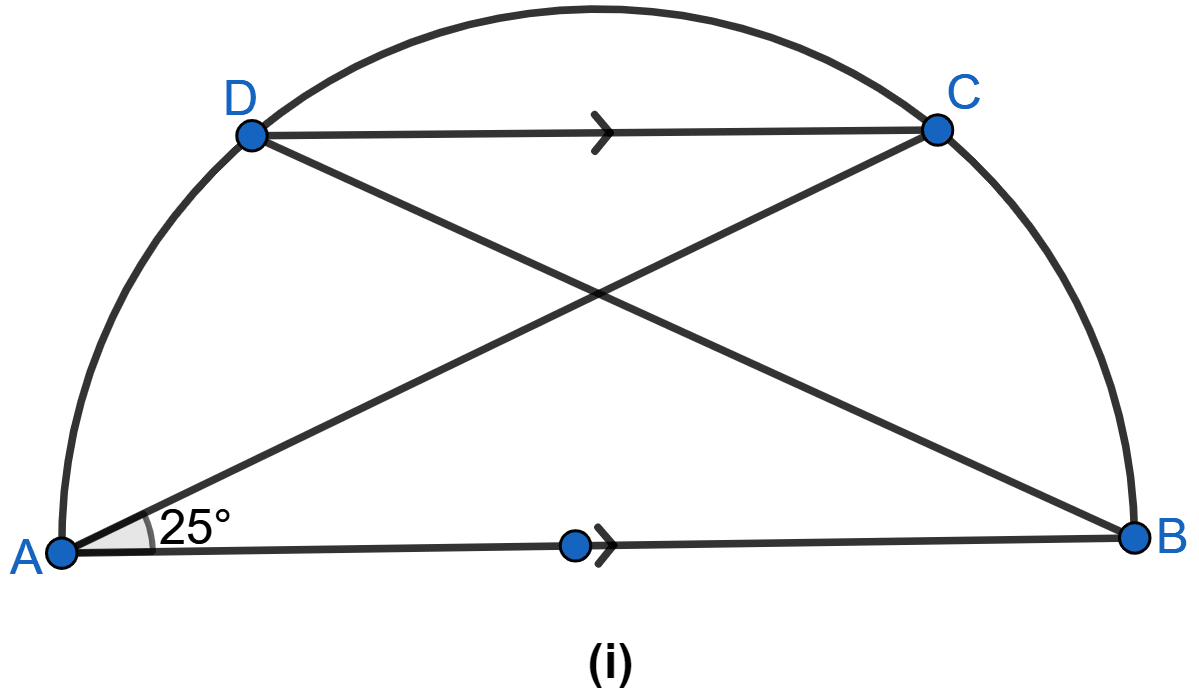
In the figure (ii) given below, O is the centre of the circle. Prove that x + y = z.
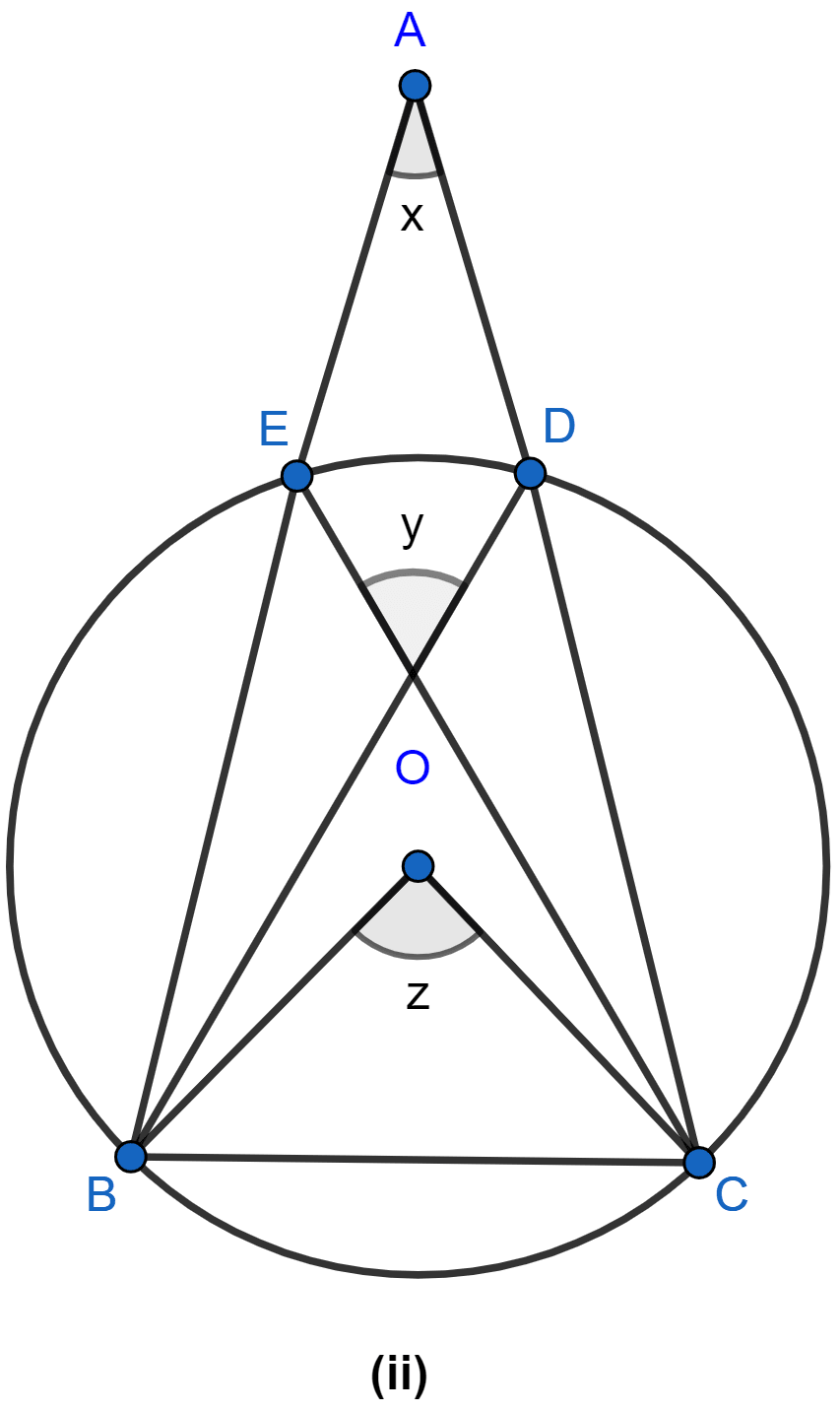
In the figure (i) given below, AB is diameter of a circle. If DC is parallel to AB and ∠CAB = 25°, find (i) ∠ADC (ii) ∠DAC.
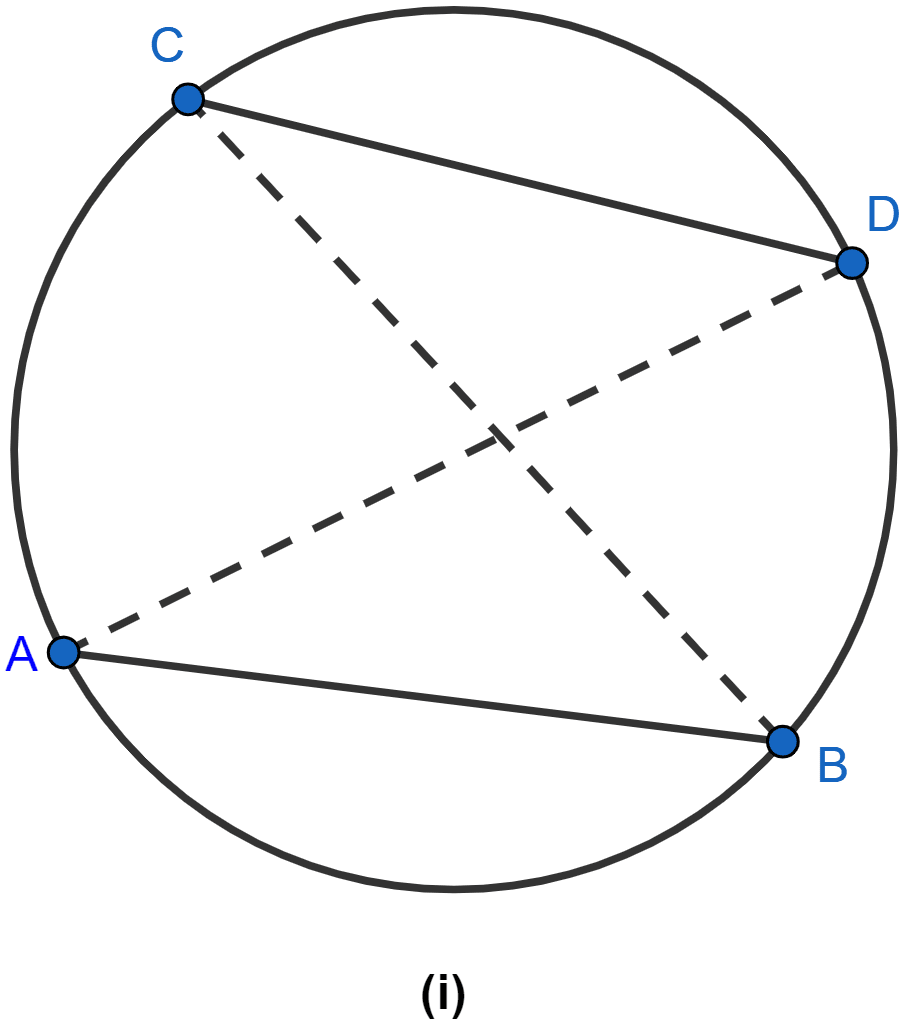
In the figure (i) given below, ABDC is a cyclic quadrilateral. If AB = CD, prove that AD = BC.
In the figure (ii) given below, ABC is an isosceles triangle with AB = AC. If ∠ABC = 50°, find ∠BDC and ∠BEC.
