Mathematics
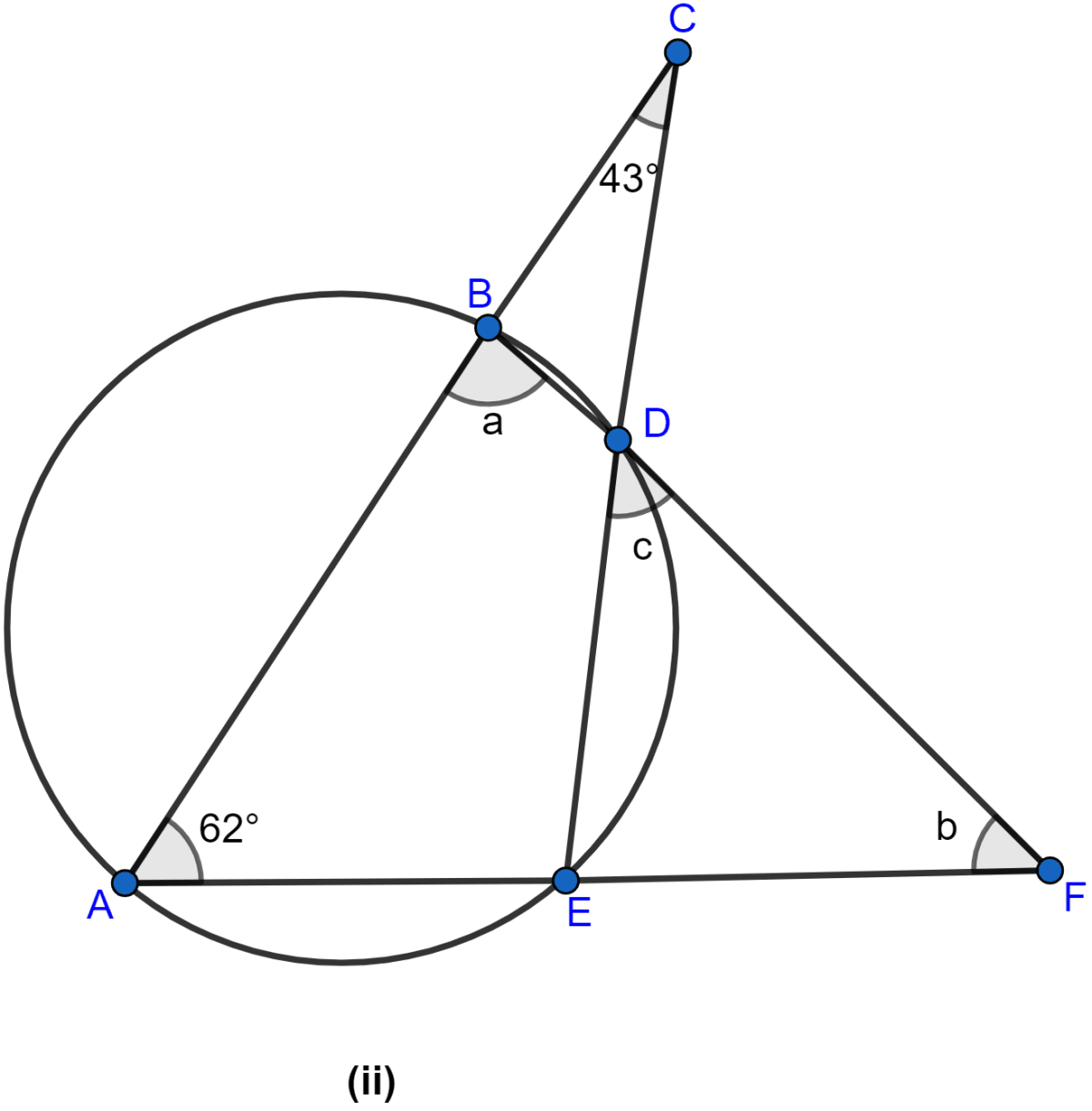
In the figure (ii) given below, if ∠ACE = 43° and ∠CAF = 62°, find the values of a, b and c.
Answer
From figure,
∠CAE = ∠CAF = 62°
Since sum of angles in triangle is 180°.
In △ACE,
⇒ ∠CAE + ∠ACE + ∠CEA = 180°
⇒ 62° + 43° + ∠CEA = 180°
⇒ ∠CEA + 105° = 180°
⇒ ∠CEA = 180° - 105°
⇒ ∠CEA = 75°.
From figure,
⇒ ∠CEA + ∠DEF = 180° (As they are linear pair.)
⇒ 75° + ∠DEF = 180°
⇒ ∠DEF = 180° - 75°
⇒ ∠DEF = 105°.
ABDE is a cyclic quadrilateral as all of its vertices lie on the circumference of the circle.
Since exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.
⇒ ∠ABD = ∠DEF = 105°
⇒ a = 105°.
Since sum of angles in triangle is 180°.
In △ABF,
⇒ ∠BAF + ∠ABF + ∠BFA = 180°
⇒ 62° + a + b = 180°
⇒ 62° + 105° + b = 180°
⇒ b + 167° = 180°
⇒ b = 180° - 167°
⇒ b = 13°
Since exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.
⇒ ∠EDF = ∠BAE = 62°
⇒ c = 62°.
Hence, the value of a = 105°, b = 13° and c = 62°.
Related Questions
In the figure (ii) given below, two circles intersect at points P and Q. If ∠A = 80° and ∠D = 84°, calculate
(i) ∠QBC
(ii) ∠BCP

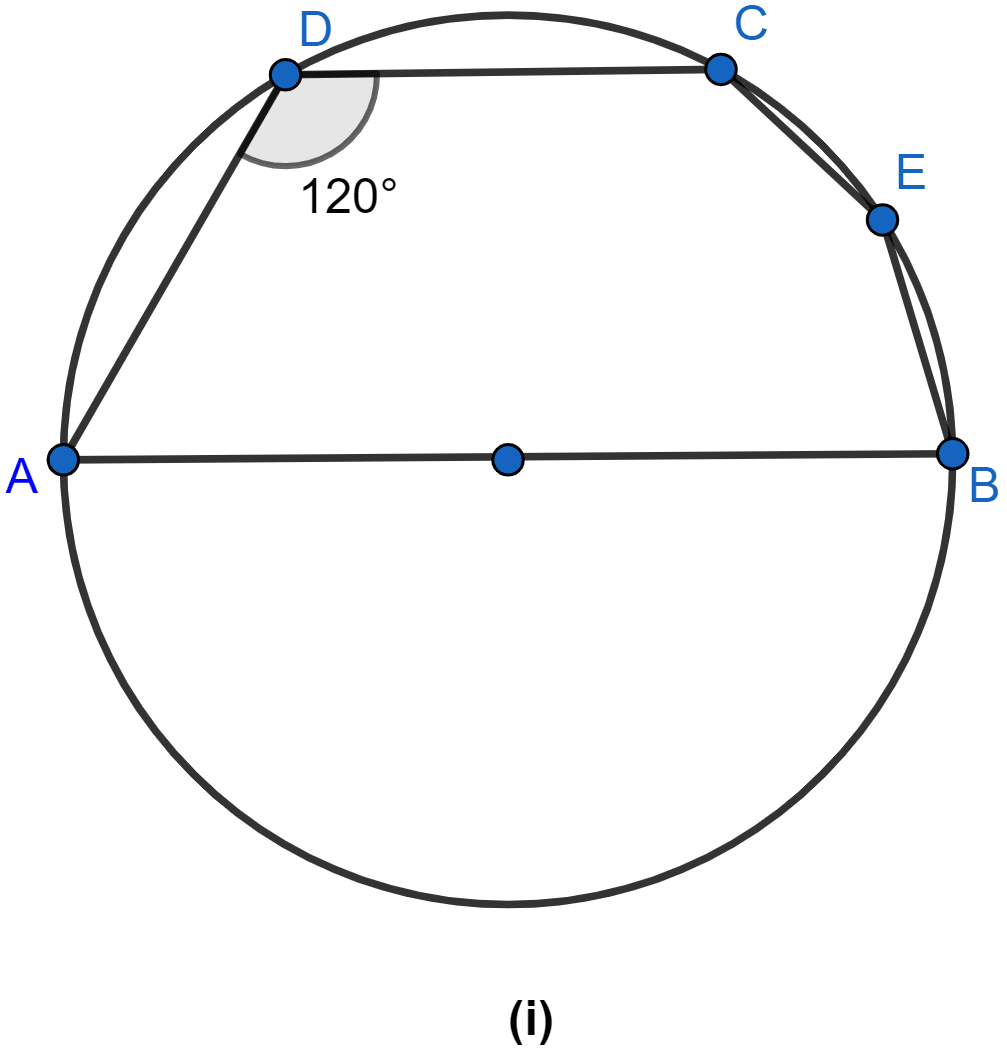
In the figure (i) given below, AB is a diameter of the circle. If ∠ADC = 120°, find ∠CAB.
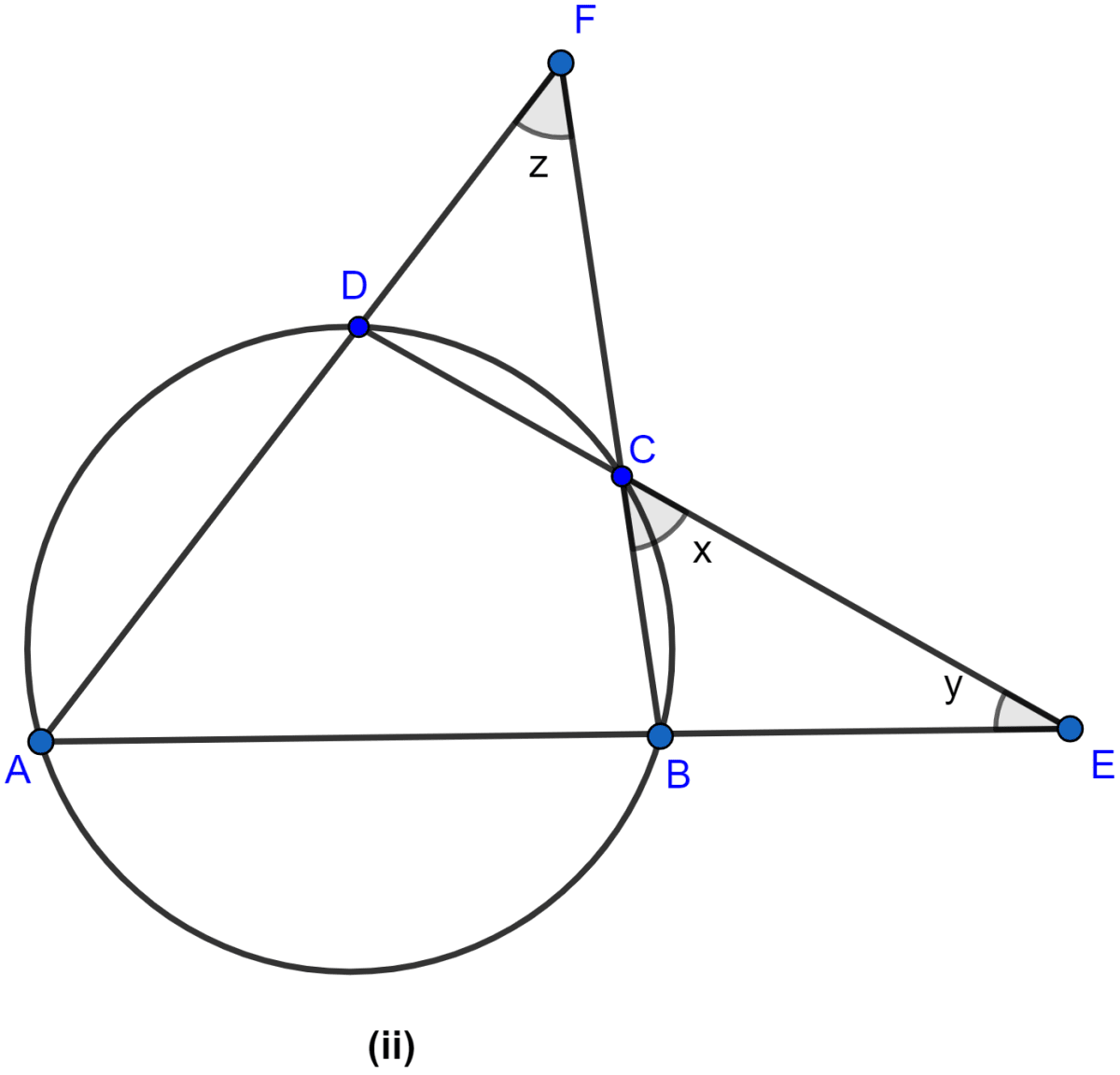
In the figure (ii) given below, sides AB and DC of a cyclic quadrilateral ABCD are produced to meet at E, the sides AD and BC are produced to meet at F. If x : y : z = 3 : 4 : 5, find the values of x, y and z.
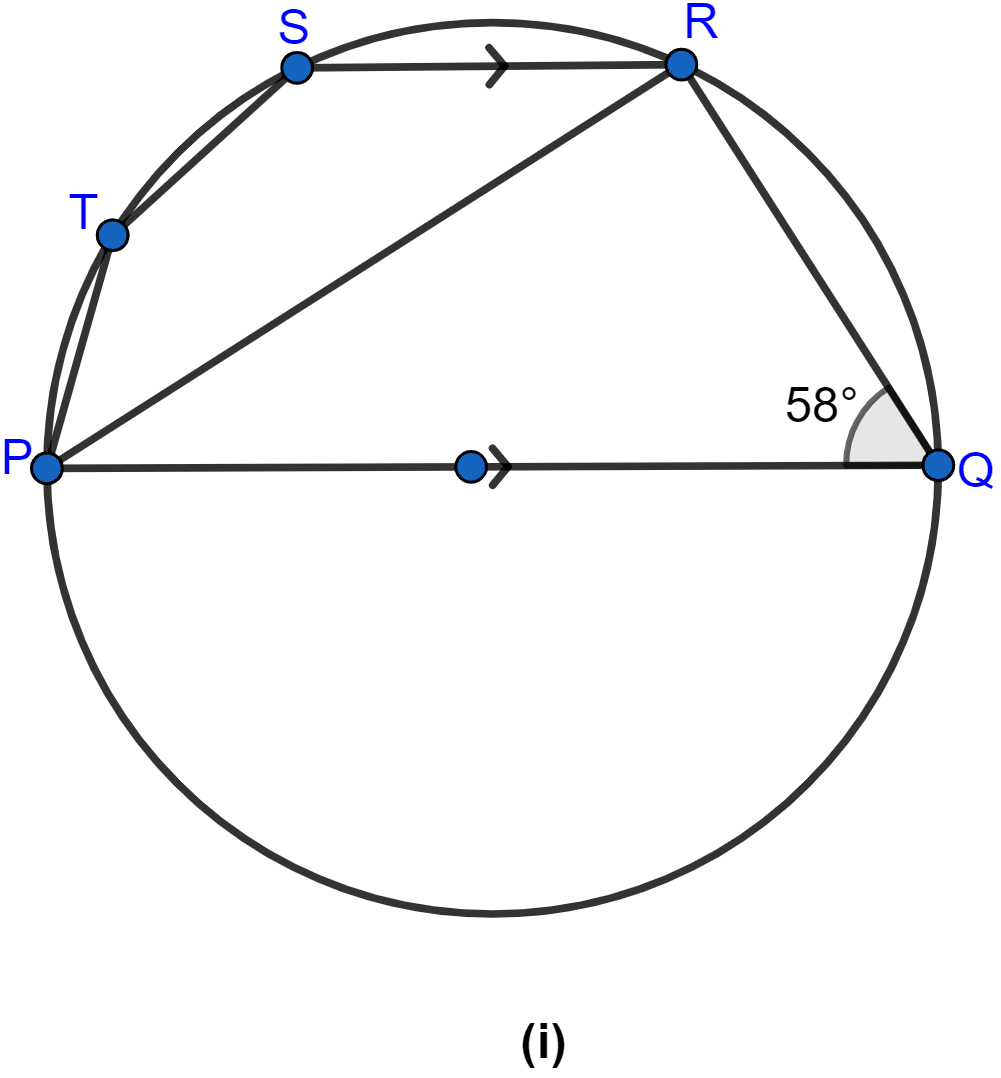
In the figure (i) given below, PQ is a diameter. Chord SR is parallel to PQ. Given ∠PQR = 58°, calculate
(i) ∠RPQ
(ii) ∠STP
(T is a point on the minor arc SP)