Mathematics
In the figure (ii) given below, chord AB and diameter CD of a circle meet at P. If AB = 8 cm, BP = 6 cm and PD = 4 cm, find the radius of the circle. Also find the length of the tangent drawn from P to the circle.

Circles
4 Likes
Answer
We know that if a chord and a tangent intersect externally, then the product of the lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.
∴ PA.PB = PT2 …..(i)
From figure,
PA = AB + PB = 8 + 6 = 14 cm.
Putting values in equation (i),
14 x 6 = PT2
PT2 = 84
PT = cm.
Joining OT as shown in the figure below:

In △OTP,
OT ⊥ TP (∵ tangents and radius at a point of contact are perpendicular to each other.)
In right angled triangle OTP,
Since, OD = OT = radius of circle = r.
Hence, the radius of the circle = 8.5 cm and length of tangent = cm.
Answered By
2 Likes
Related Questions
In the adjoining figure, chord AB and diameter PQ of a circle with centre O meet at X. If BX = 5 cm, OX = 10 cm and the radius of the circle is 6 cm, compute the length of AB. Also find the length of tangent drawn from X to the circle.
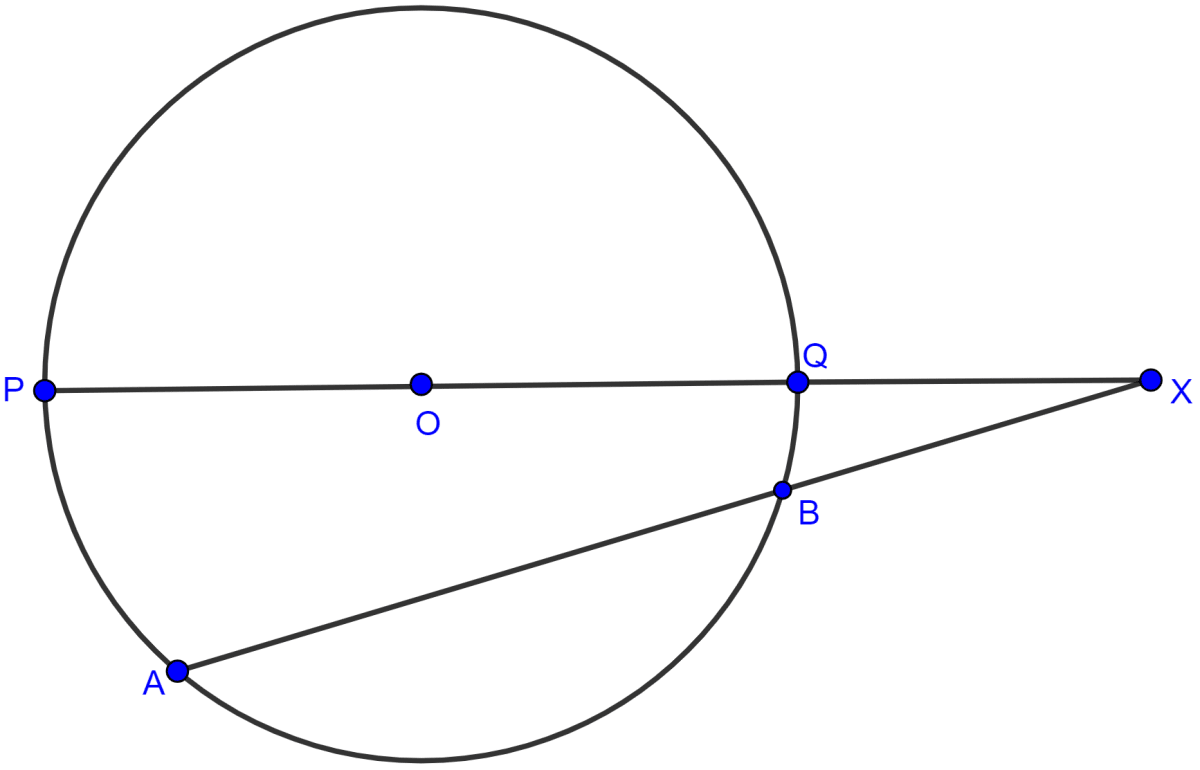
Two chords AB, CD of a circle intersect externally at a point P. If PB = 7 cm, AB = 9 cm and PD = 6 cm, find CD.
In the figure (i) given below, chord AB and diameter CD of a circle with centre O meet at P. PT is tangent to the circle at T. If AP = 16 cm, AB = 12 cm and DP = 2 cm, find the length of PT and the radius of the circle.

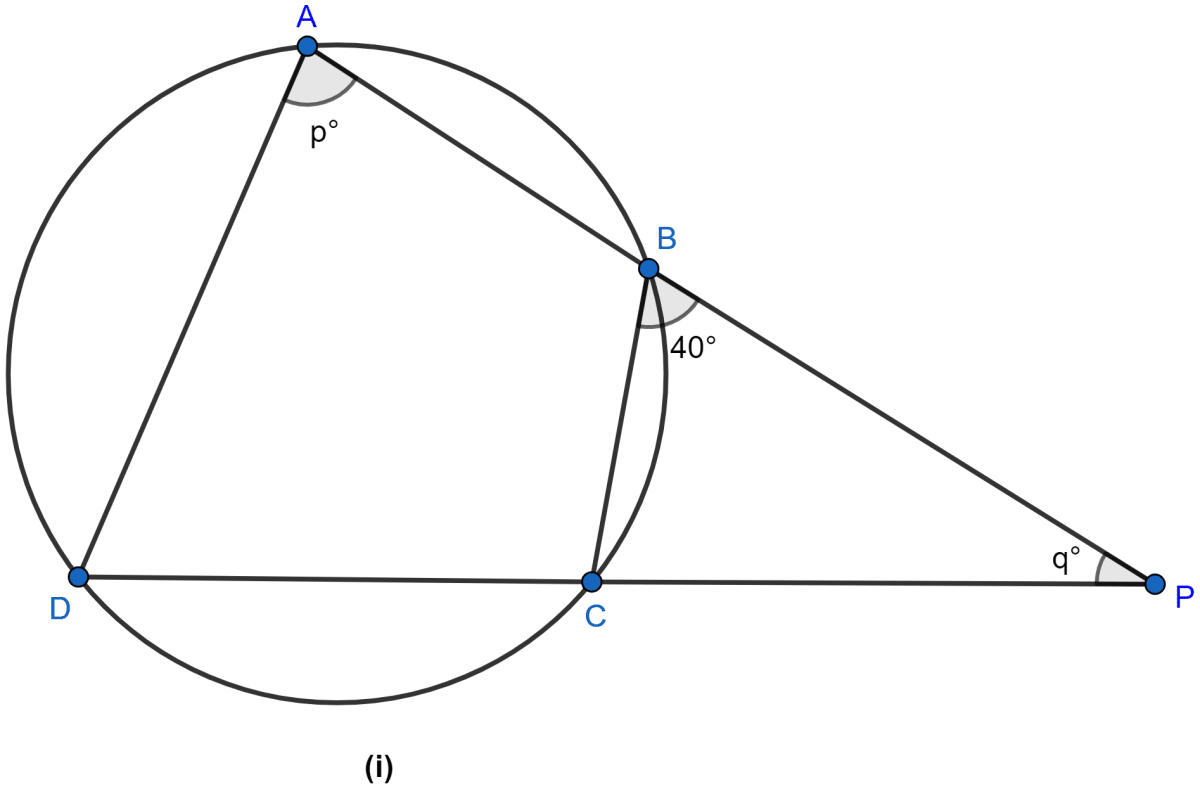
In the figure (i) given below, ∠CBP = 40°, ∠CPB = q° and ∠DAB = p°. Obtain an equation connecting p and q. If AC and BD meet at Q so that ∠AQD = 2q° and the points C, P, B and Q are concyclic, find the values of p and q.