Mathematics
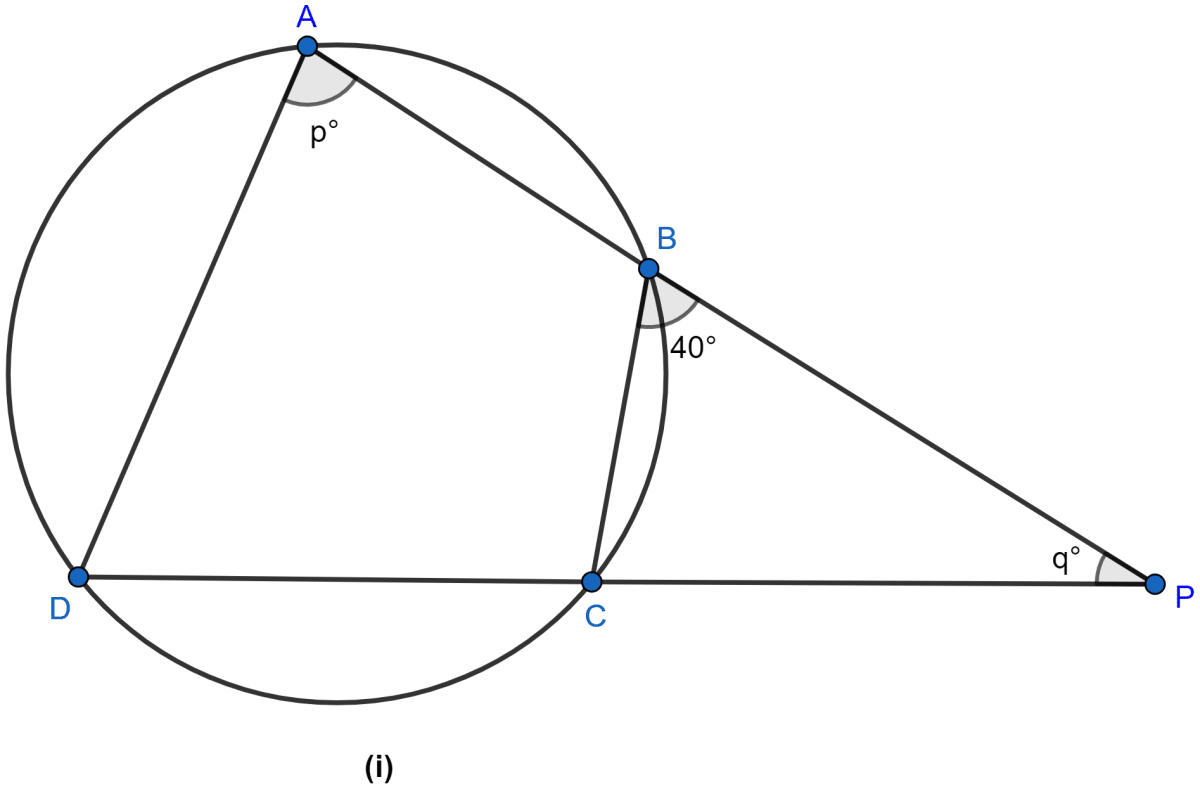
In the figure (i) given below, ∠CBP = 40°, ∠CPB = q° and ∠DAB = p°. Obtain an equation connecting p and q. If AC and BD meet at Q so that ∠AQD = 2q° and the points C, P, B and Q are concyclic, find the values of p and q.
Circles
17 Likes
Answer
From figure,
∠ADC = ∠CBP = 40°. (∵ angles in alternate segments are equal.)
Since sum of angles in a triangle = 180°.
In △ADP,
∠DAP + ∠APD + ∠ADP = 180°
From figure, ∠ADP = ∠ADC = 40°.
⇒ p° + q° + 40° = 180°
⇒ p° + q° = 180° - 40°
⇒ p° + q° = 140° …..(i)
Join AC and BD as shown in the figure below:
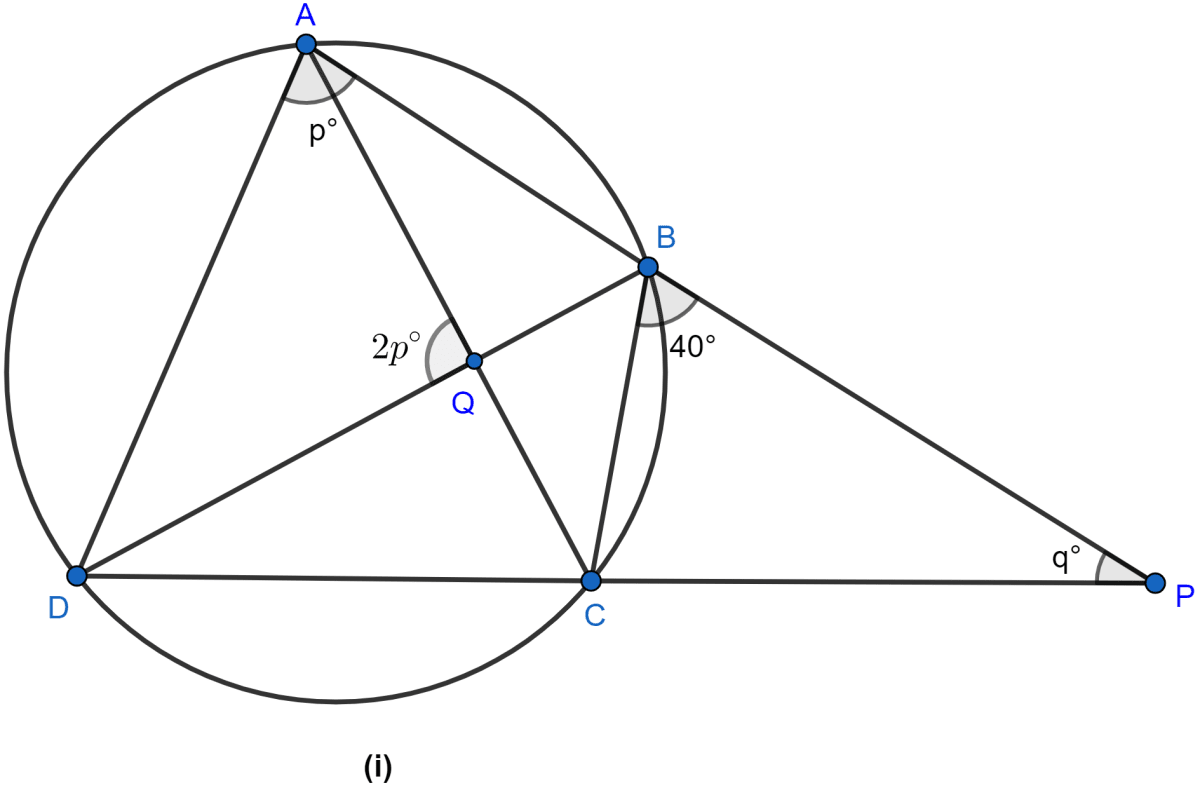
∠CQB = ∠AQD = 2q° (∵ vertically opposite angles are equal.)
Given C, P, B, Q are concyclic.
∴ ∠CPB + ∠CQB = 180°
⇒ q° + 2q° = 180°
⇒ 3q° = 180°
⇒ q° = 60°.
Putting value of q in equation (i) we get,
⇒ p° + 60° = 140°
⇒ p° = 140° - 60° = 80°.
Hence, the value of p = 80 and q = 60 and the relation between p and q is p + q = 140.
Answered By
10 Likes
Related Questions
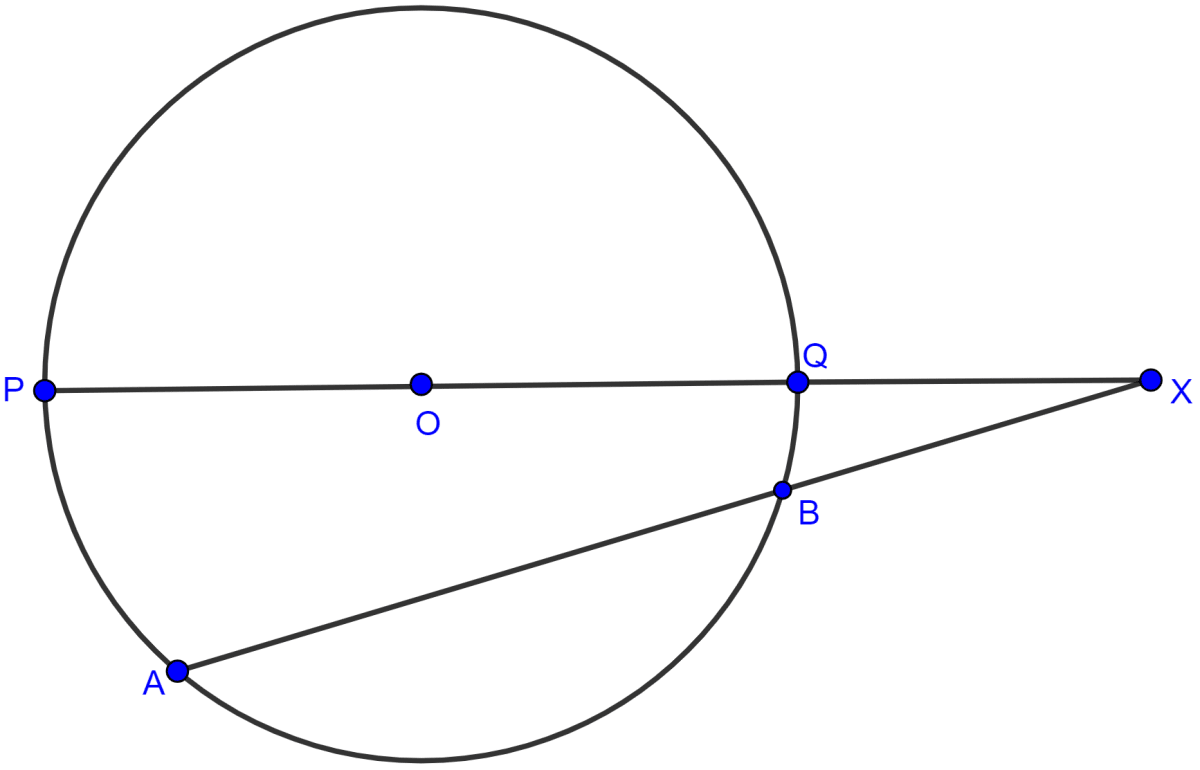
In the adjoining figure, chord AB and diameter PQ of a circle with centre O meet at X. If BX = 5 cm, OX = 10 cm and the radius of the circle is 6 cm, compute the length of AB. Also find the length of tangent drawn from X to the circle.
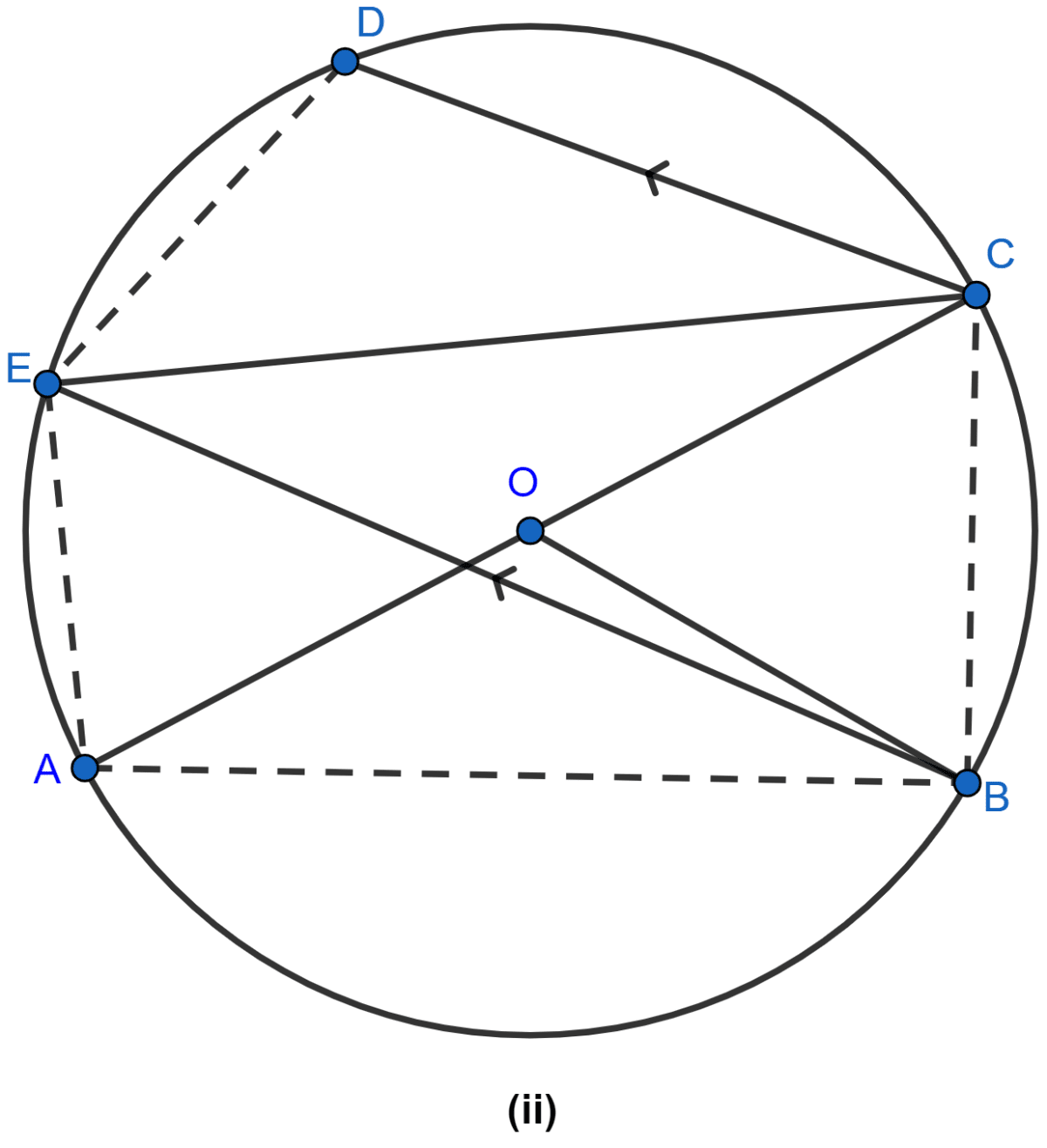
In the figure (ii) given below, AC is a diameter of the circle with centre O. If CD || BE, ∠AOB = 130° and ∠ACE = 20°, find :
(i) ∠BEC
(ii) ∠ACB
(iii) ∠BCD
(iv) ∠CED.
In the figure (i) given below, chords AB, BC and CD of a circle with center O are equal. If ∠BCD = 120°, find
(i) ∠BDC
(ii) ∠BEC
(iii) ∠AEB
(iv) ∠AOB.
Hence, prove that △OAB is equilateral.
In the figure (ii) given below, chord AB and diameter CD of a circle meet at P. If AB = 8 cm, BP = 6 cm and PD = 4 cm, find the radius of the circle. Also find the length of the tangent drawn from P to the circle.
