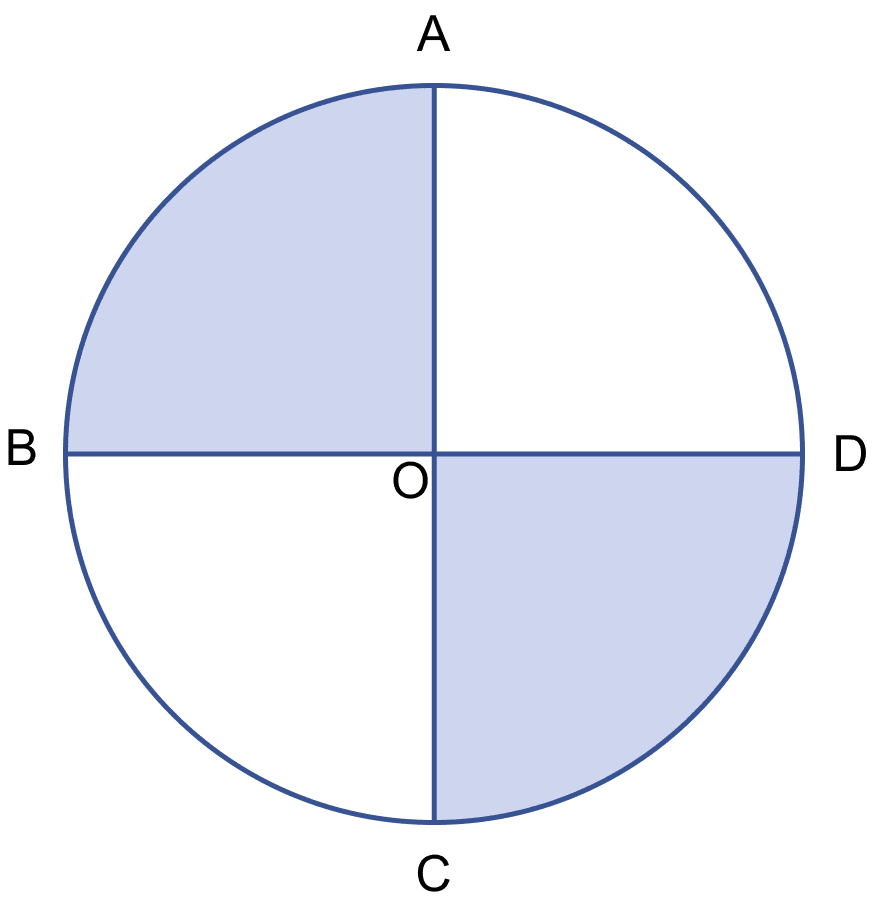
In the figure (ii) given below, AC and BD are two perpendicular diameters of a circle with center O. If AC = 16 cm, calculate the area and perimeter of the shaded part. (Take π = 3.14)

Given,

AC = 16 cm, AO = $\dfrac{AC}{2} = \dfrac{16}{2}$ = 8 cm.

The diameters of the circle divide circle into 4 quadrants.

Area of each quadrant = $\dfrac{πr^2}{4}$

$= \dfrac{3.14 \times 8^2}{4} \\[1em] = \dfrac{3.14 \times 64}{4} \\[1em] = 3.14 \times 16 \\[1em] = 50.24 \text{ cm}^2.$

Area of quadrant AOD + Area of quadrant BOC = 50.24 + 50.24 = 100.48 cm².

Perimeter of each quadrant = $\dfrac{2πr}{4} + r + r = \dfrac{πr}{2} + 2r$

$= \dfrac{3.14 \times 8}{2} + (2 \times 8) \\[1em] = \dfrac{25.12}{2} + 16 \\[1em] = 12.56 + 16 \\[1em] = 28.56 \text{ cm}^2.$

Perimeter of both quadrants = 2 × 28.56 = 57.12 cm.

Hence, area of shaded region = 100.48 cm² and perimeter of shaded region = 57.12 cm.