Mathematics
A bucket is raised from a well by means of a rope which is wound round a wheel of diameter 77 cm. Given that the bucket ascends in 1 minute 28 seconds with a uniform speed of 1.1 m/sec, calculate the number of complete revolutions the wheel makes in raising the bucket.
Mensuration
60 Likes
Answer
Time in which bucket ascends = 1 minute 28 seconds = 60 + 28 = 88 seconds.
Speed of bucket = 1.1 m/sec
Distance covered by bucket while ascending = Speed × Time = 1.1 × 88 = 96.8 m.
Radius of wheel = = 38.5 cm.
Circumference of circle = 2πr = = 242 cm = 2.42 m.
Let n be the no. of revolutions of wheel.
Distance covered by bucket = Distance covered by wheel
⇒ 96.8 = 2.42 × n
⇒ n = = 40.
Hence, wheel makes 40 revolutions in raising the bucket.
Answered By
38 Likes
Related Questions
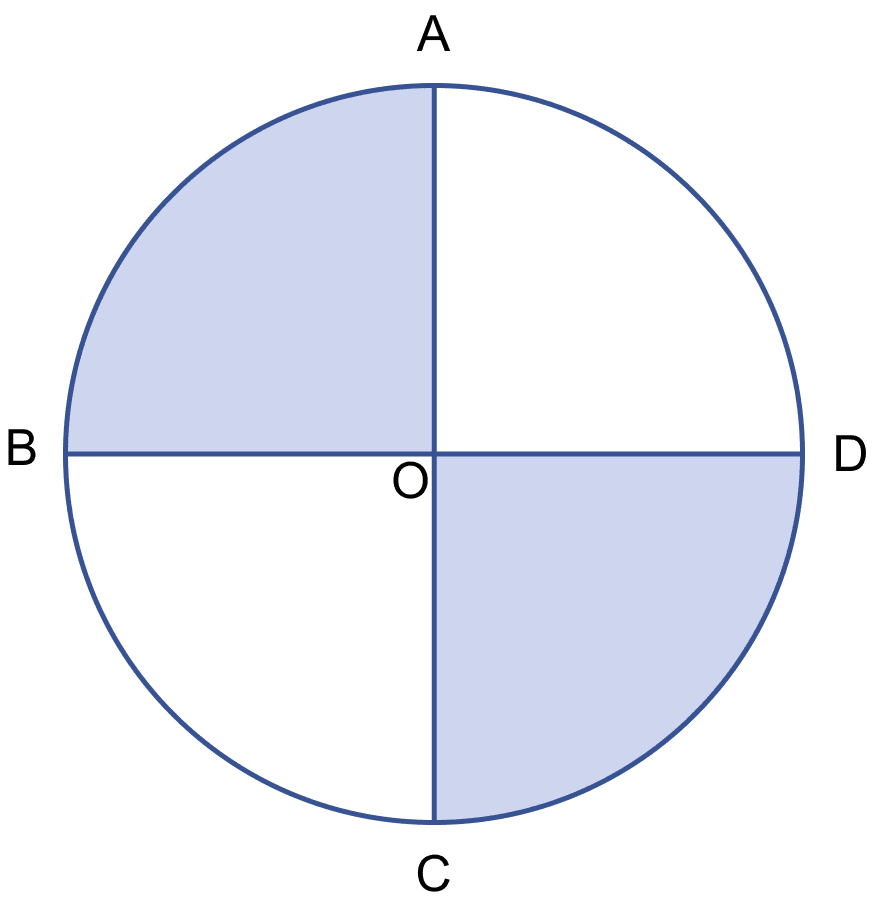
In the figure (i) given below, AC and BD are two perpendicular diameters of a circle ABCD. Given that the area of shaded portion is 308 cm2, calculate :
(i) the length of AC and
(ii) the circumference of the circle.

In the figure (ii) given below, AC and BD are two perpendicular diameters of a circle with center O. If AC = 16 cm, calculate the area and perimeter of the shaded part. (Take π = 3.14)
The wheel of a cart is making 5 revolutions per second. If the diameter of the wheel is 84 cm, find its speed in km/hr. Give your answer, correct to the nearest km.
The circumference of a circle is 123.2 cm. Calculate :
(i) the radius of the circle in cm.
(ii) the area of the circle in cm2, correct to nearest cm2.
(iii) the effect on the area of the circle if the radius is doubled.