Mathematics
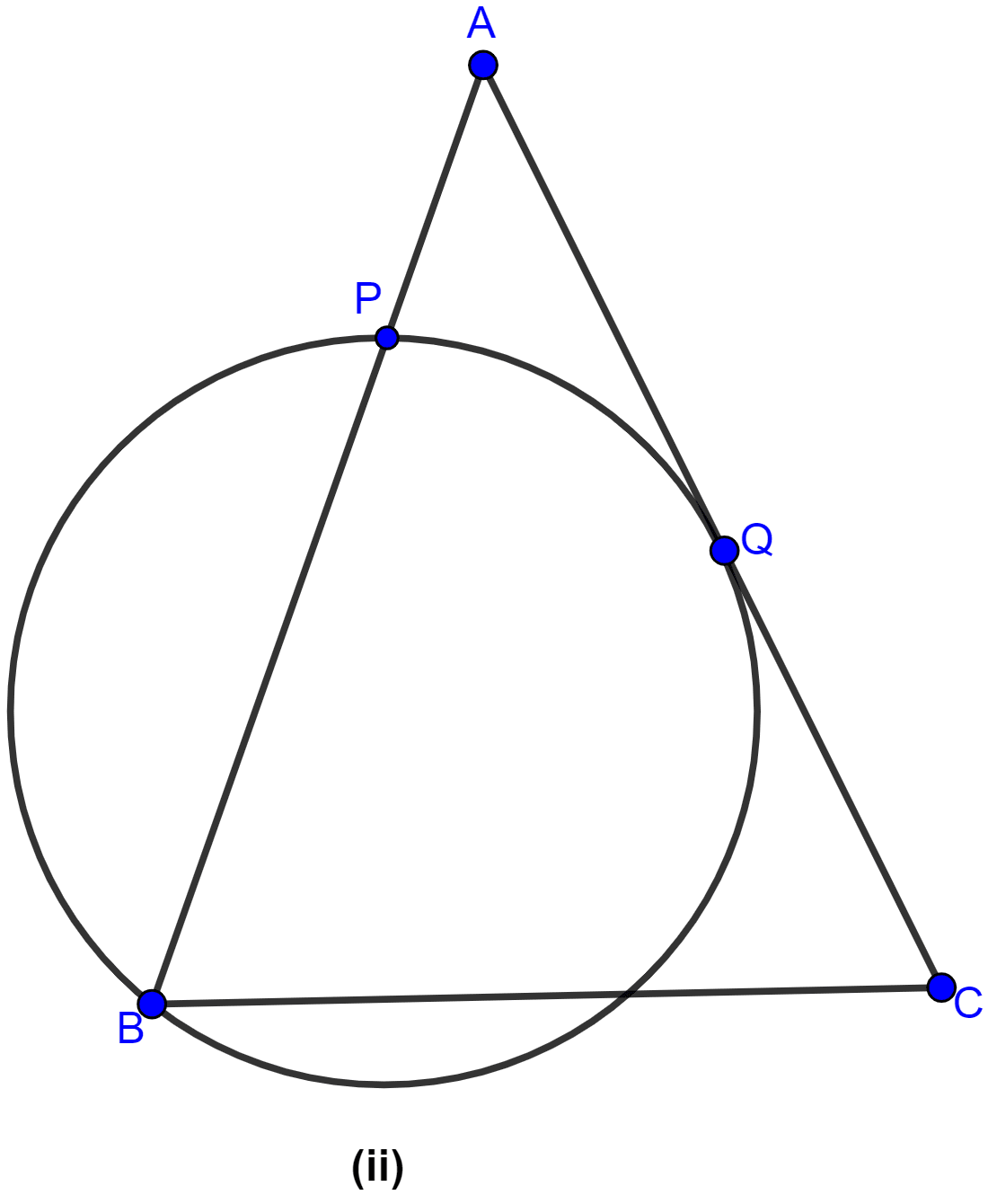
In the figure (ii) given below, ABC is an isosceles triangle in which AB = AC and Q is mid-point of AC. If APB is a secant and AC is tangent to the circle at Q, prove that AB = 4AP.
Related Questions
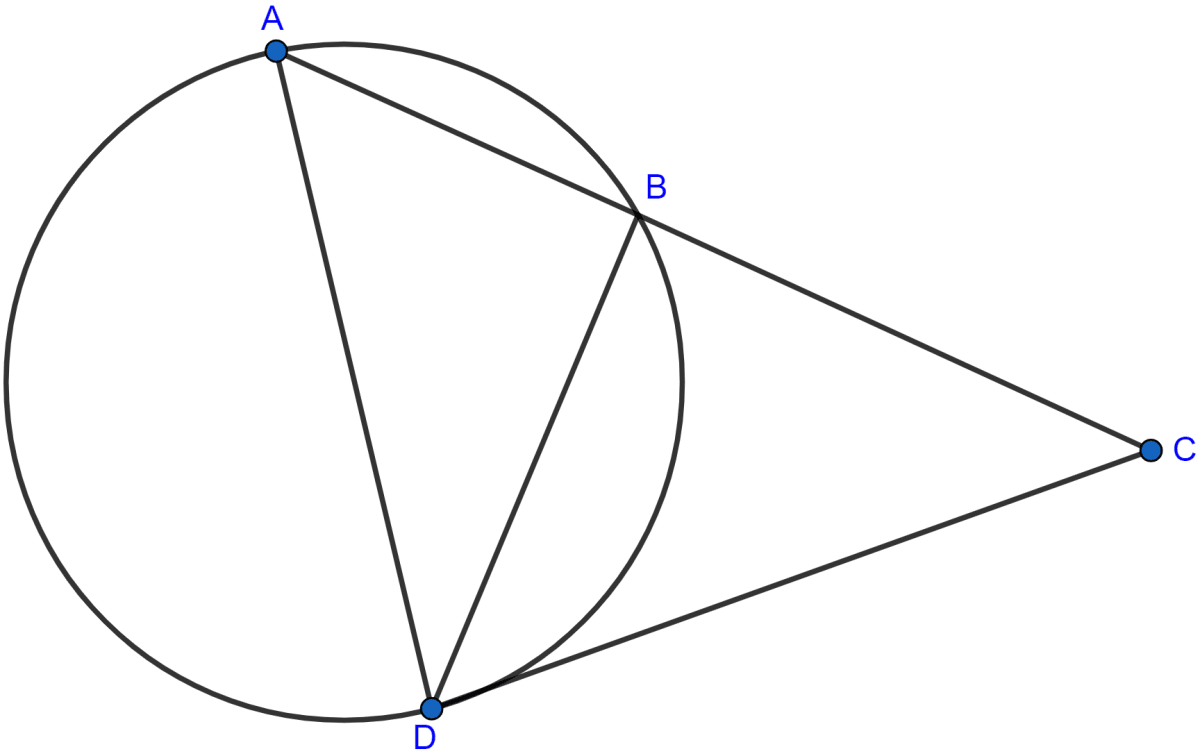
In the adjoining figure, CBA is a secant and CD is tangent to the circle. If AB = 7 cm and BC = 9 cm, then
(i) Prove that △ACD ~ △DCB
(ii) find the length of CD.
In the figure (i) given below, AT is tangent to a circle at A. If ∠BAT = 45° and ∠BAC = 65°, find ∠ABC.
Two chords AB, CD of a circle intersect externally at a point P. If PA = PC, prove that AB = CD.
In the figure (i) given below, PAB is a secant and PT is tangent to a circle. If PA : AB = 1 : 3 and PT = 6 cm, find the length of PB.
