Mathematics
In the figure (i) given below, AT is tangent to a circle at A. If ∠BAT = 45° and ∠BAC = 65°, find ∠ABC.

Circles
18 Likes
Answer
From figure,
∠ACB = ∠BAT = 45° (∵ angles in alternate segments are equal)
Since sum of angles in a triangle = 180°.
In △ABC,
⇒ ∠ACB + ∠CAB + ∠ABC = 180°
⇒ 45° + 65° + ∠ABC = 180°
⇒ 110° + ∠ABC = 180°
⇒ ∠ABC = 180° - 110°
⇒ ∠ABC = 70°.
Hence, the value of ∠ABC = 70°.
Answered By
8 Likes
Related Questions
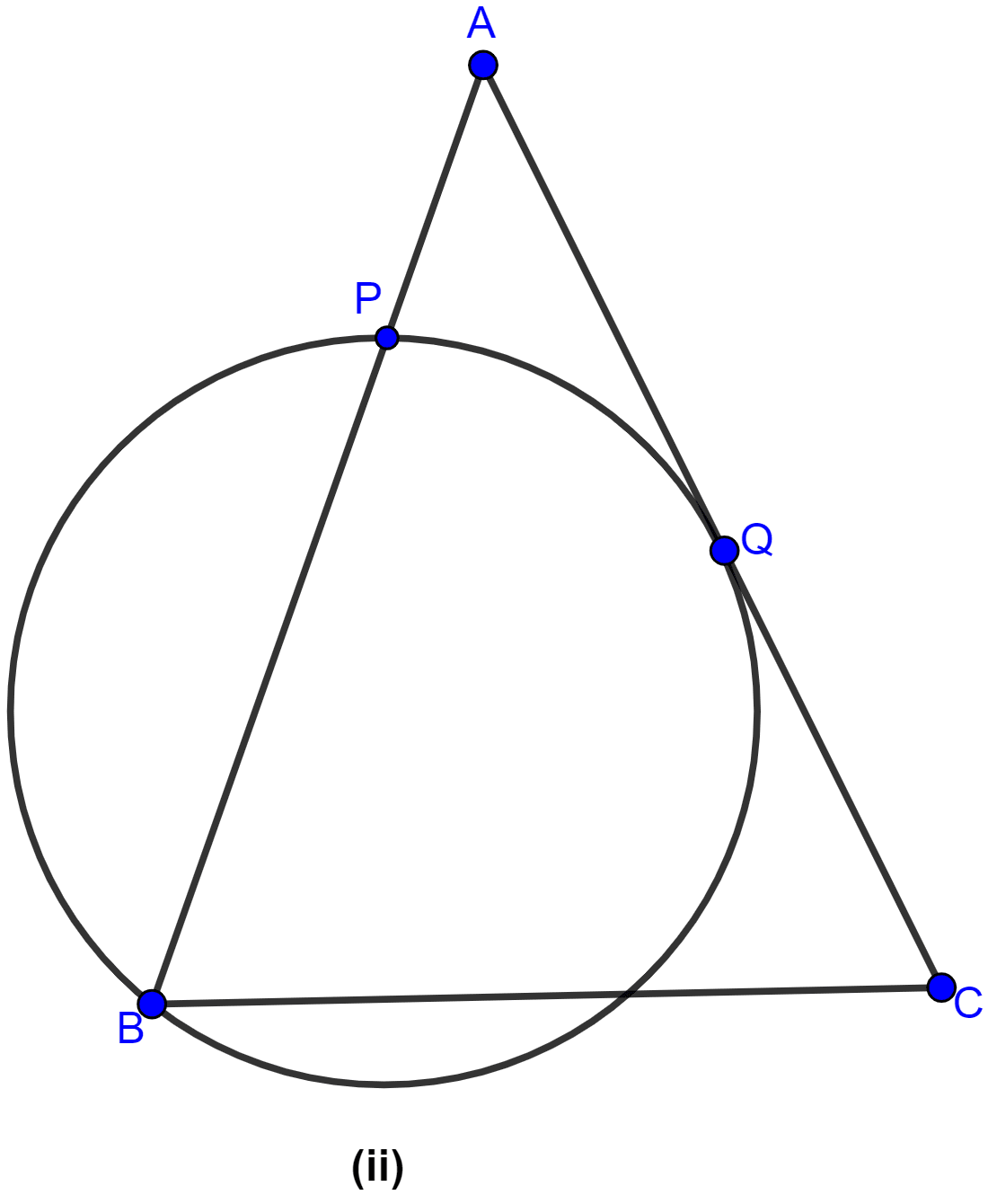
In the figure (ii) given below, ABC is an isosceles triangle in which AB = AC and Q is mid-point of AC. If APB is a secant and AC is tangent to the circle at Q, prove that AB = 4AP.
Two chords AB, CD of a circle intersect externally at a point P. If PA = PC, prove that AB = CD.
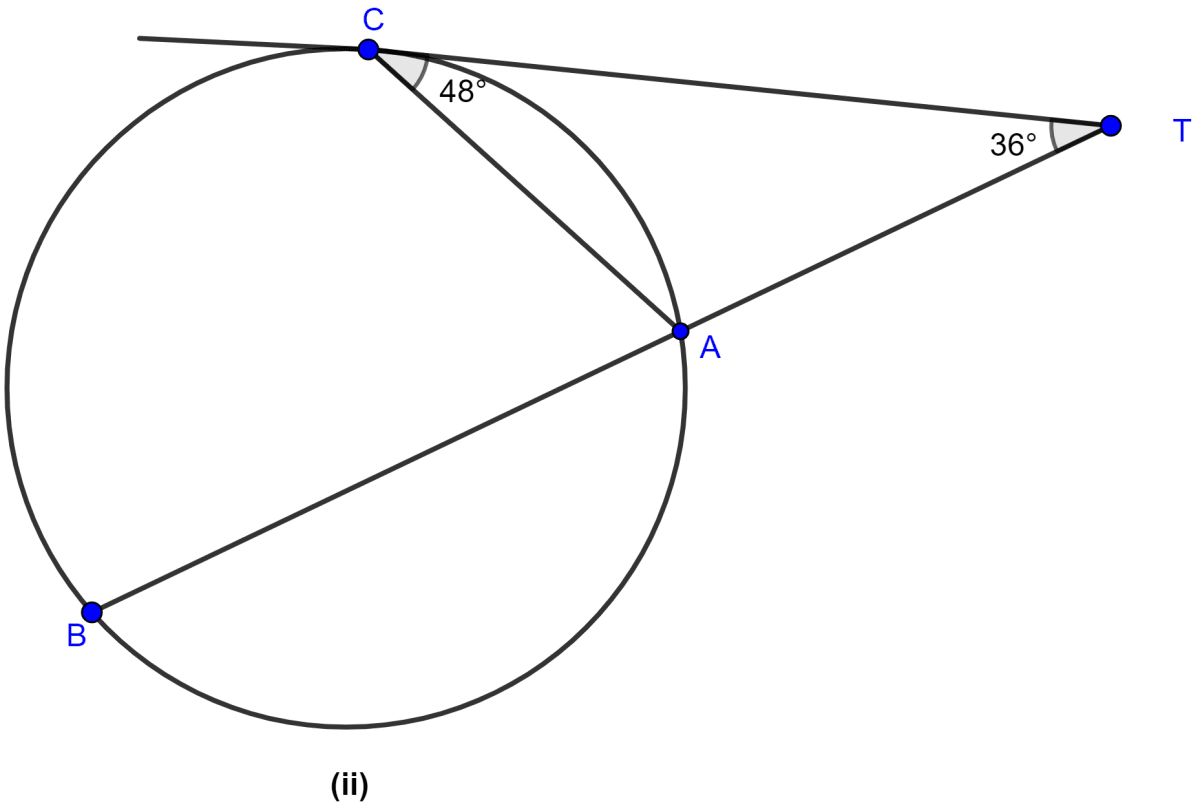
In the figure (ii) given below, A, B and C are three points on a circle. The tangent at C meets BA produced at T. Given that ∠ATC = 36° and ∠ACT = 48°, calculate the angle subtended by AB at the centre of the circle.
In the adjoining figure, △ABC is isosceles with AB = AC. Prove that the tangent at A to the circumcircle of △ABC is parallel to BC.
