Mathematics
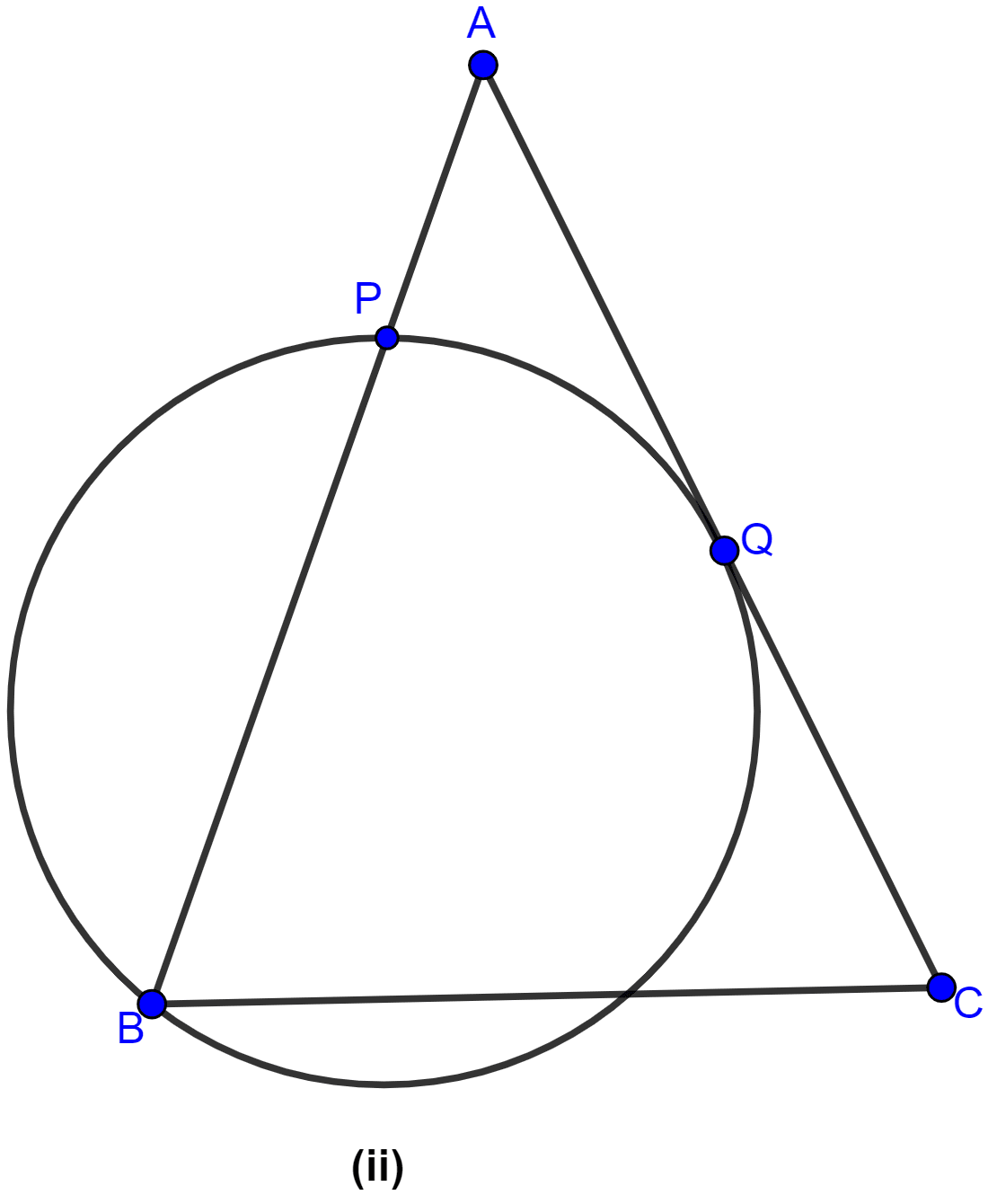
In the figure (ii) given below, ABC is an isosceles triangle in which AB = AC and Q is mid-point of AC. If APB is a secant and AC is tangent to the circle at Q, prove that AB = 4AP.
Circles
Answer
We know that,
If a chord and a tangent intersect externally, then the product of lengths of the segments of the chord is equal to the square of the length of the tangent from the point of contact to the point of intersection.
∴ AQ2 = AP × AB …..(Eq. 1)
Given Q is mid-point of AC, so AQ = .
Since, AC = AB.
Dividing both sides by AB,
AB = 4 x AP.
Hence, proved that AB = 4AP.
Answered By
Related Questions
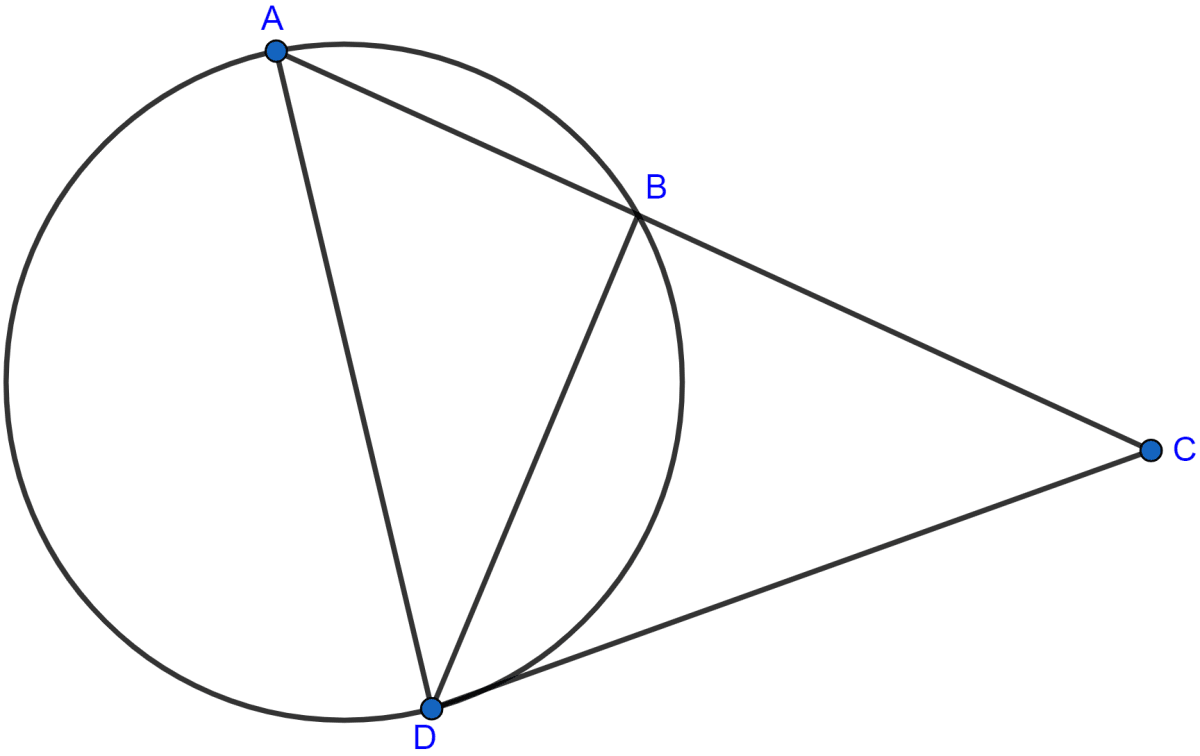
In the adjoining figure, CBA is a secant and CD is tangent to the circle. If AB = 7 cm and BC = 9 cm, then
(i) Prove that △ACD ~ △DCB
(ii) find the length of CD.
In the figure (i) given below, PAB is a secant and PT is tangent to a circle. If PA : AB = 1 : 3 and PT = 6 cm, find the length of PB.

Two chords AB, CD of a circle intersect externally at a point P. If PA = PC, prove that AB = CD.
In the figure (i) given below, AT is tangent to a circle at A. If ∠BAT = 45° and ∠BAC = 65°, find ∠ABC.
