Mathematics
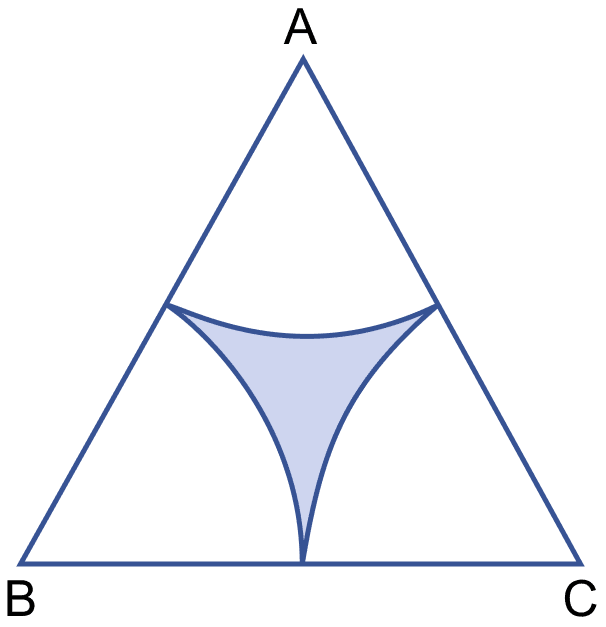
In the figure (ii) given below, ABC is an equilateral triangle of side 8 cm. A, B and C are the centers of circular arcs of equal radius. Find the area of the shaded region correct upto 2 decimal places.
Mensuration
28 Likes
Answer
We know that
△ABC is an equilateral triangle of side 8 cm
A, B, C are the centres of three circular arcs of equal radius
Radius = = 4 cm
By formula,
Area of △ABC =
= × 8 × 8
=
=
= 16 × 1.732
= 27.712 cm2.
So, the area of 3 equal sectors of 60° whose radius is 4 cm = 3 × πr2 ×
= 3 × 3.142 × 4 × 4 ×
= 3.142 × 8
= 25.136 cm2.
Area of shaded region = Area of equilateral triangle - Area of 3 sectors
= 27.712 – 25.136
= 2.576 ≈ 2.58 cm2.
Hence, area of shaded region = 2.58 cm2.
Answered By
15 Likes
Related Questions
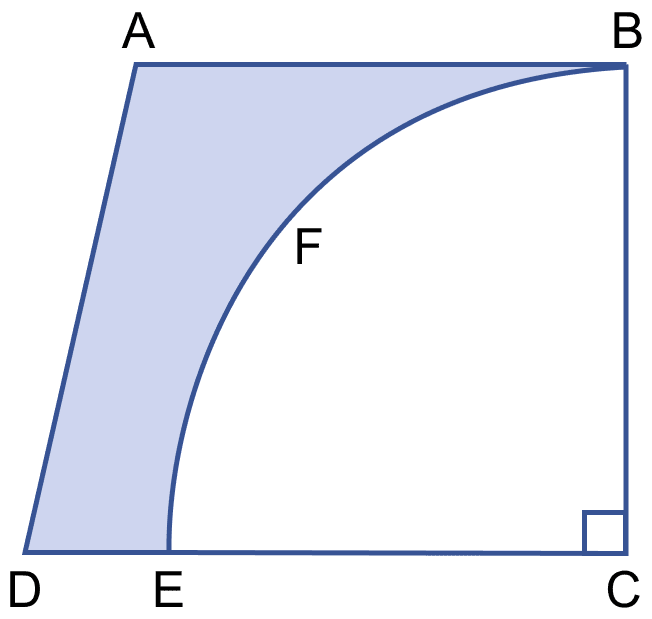
In the figure (ii) given below, a piece of cardboard, in the shape of a trapezium ABCD and AB || CD and ∠BCD = 90°, quarter circle BFEC is removed. Given AB = BC = 3.5 cm and DE = 2 cm. Calculate the area of the remaining piece of the cardboard.
In the figure (i) given below, ABC is a right angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semi-circle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.

A circle is inscribed in a regular hexagon of side cm. Find
(i) the circumference of the inscribed circle
(ii) the area of the inscribed circle
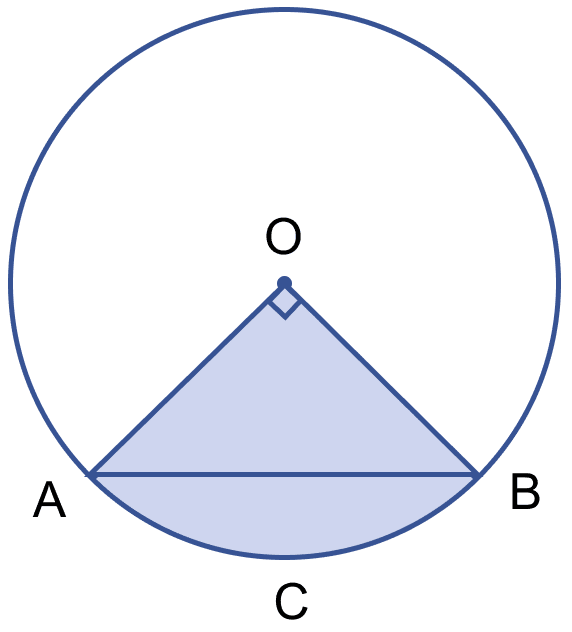
In the adjoining figure, a chord AB of a circle of radius 10 cm subtends a right angle at the centre O. Find the area of the sector OACB and of the major segment. Take π = 3.14.