Mathematics
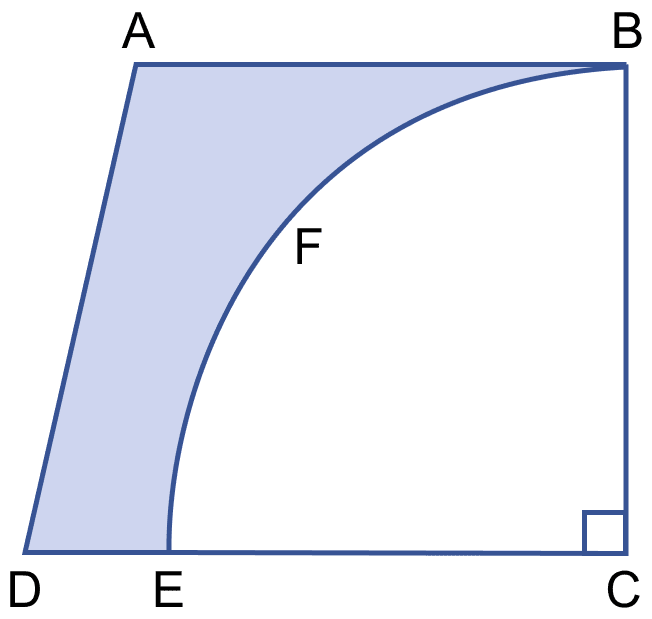
In the figure (ii) given below, a piece of cardboard, in the shape of a trapezium ABCD and AB || CD and ∠BCD = 90°, quarter circle BFEC is removed. Given AB = BC = 3.5 cm and DE = 2 cm. Calculate the area of the remaining piece of the cardboard.
Mensuration
13 Likes
Answer
From figure,
Radius of quadrant = BC = 3.5 cm.
EC = BC = 3.5 cm (As both equal to radius of quadrant BFEC)
By formula,
Area of trapezium = × (Sum of || sides) × distance between them
= × (AB + DC) × BC
= × (AB + EC + DE) × BC
= × (3.5 + 3.5 + 2) × 3.5
= × 9 × 3.5
= 4.5 × 3.5
= 15.75 cm2.
So, the area of quadrant BCEF =
Area of shaded portion = Area of trapezium - Area of quadrant
= 15.75 – 9.625 = 6.125 cm2.
Hence, area of shaded portion = 6.125 cm2.
Answered By
12 Likes
Related Questions
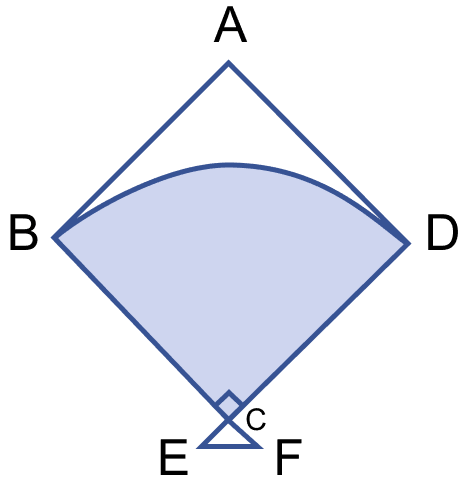
The figure (ii) given below shows a kite, in which BCD is in the shape of a quadrant of a circle of radius 42 cm. ABCD is a square and △CEF is an isosceles right angled triangle whose equal sides are 6 cm long. Find the area of the shaded region.
In the figure (i) given below, the boundary of the shaded region in the given diagram consists of four semicircular arcs, the smallest two being equal. If the diameter of the largest is 14 cm and of the smallest is 3.5 cm, calculate
(i) the length of the boundary.
(ii) the area of the shaded region.

In the figure (i) given below, ABC is a right angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semi-circle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.

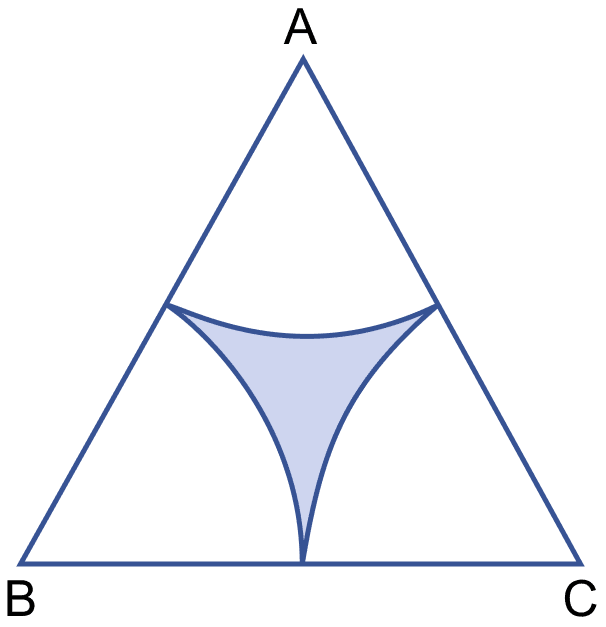
In the figure (ii) given below, ABC is an equilateral triangle of side 8 cm. A, B and C are the centers of circular arcs of equal radius. Find the area of the shaded region correct upto 2 decimal places.