Mathematics
A circle is inscribed in a regular hexagon of side cm. Find
(i) the circumference of the inscribed circle
(ii) the area of the inscribed circle
Mensuration
24 Likes
Answer
(i) Side of the regular hexagon (a) = cm.
Now since a regular hexagon has 6 sides, hence we can say the central angle of a hexagon = = 60°.
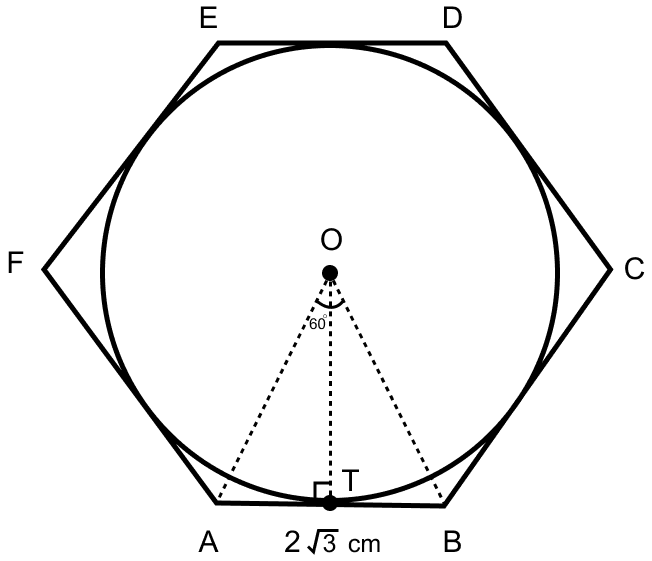
From figure,
∠AOB = 60°.
Now in the ΔAOB,
Since the total sum of the angles of a triangle is equal to 180°
∴ ∠AOB + ∠OAB + ∠OBA = 180° …….(1)
Since, OA = OB = radius of circle,
So, ∠OAB = ∠OBA = x (let) (Angles opposite to equal sides are equal).
Substituting value in equation 1 we get,
⇒ 60° + x + x = 180°
⇒ 2x + 60° = 180°
⇒ 2x = 120°
⇒ x = 60°.
Now since all the angles of the triangle are equal hence we can say the triangle is an equilateral triangle. So, all the sides of the triangle will also be equal.
∴ AO = BO = AB = cm.
Draw perpendicular from O to AB.
From figure,
AT = BT = cm. (As altitude and median are same in equilateral triangle.)
From figure,
In right angle triangle OAT,
Hence, radius of circle = OT = 3 cm.
We know the circumference of a circle is given by the formula,
Circumference = 2πr
=
= cm.
Hence, circumference of inscribed circle = cm.
(ii) Area of inscribed circle = πr2
=
= cm2.
Hence, area of inscribed circle = cm2.
Answered By
17 Likes
Related Questions
In the figure (i) given below, ABC is a right angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm. With AC as diameter a semi-circle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.

In the figure (ii) given below, ABC is an equilateral triangle of side 8 cm. A, B and C are the centers of circular arcs of equal radius. Find the area of the shaded region correct upto 2 decimal places.
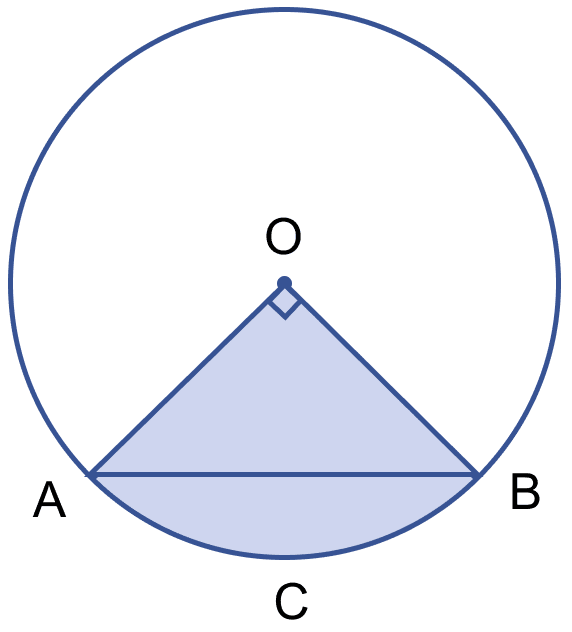
In the adjoining figure, a chord AB of a circle of radius 10 cm subtends a right angle at the centre O. Find the area of the sector OACB and of the major segment. Take π = 3.14.
Find the surface area and volume of a cube whose one edge is 7 cm.